
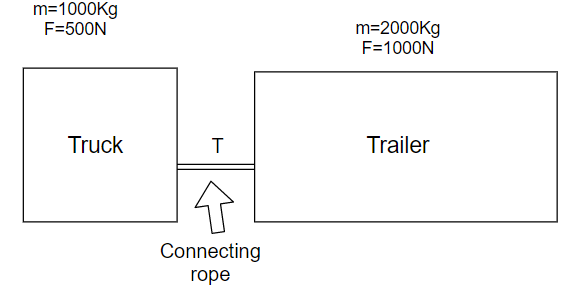
A truck of mass $1000\,Kg$ is pulling a trailer of mass $2000\,Kg$ frictional force on truck is $500\,N$ and on trailer is $1000\,N$. The truck extra force of $6000\,N$. Calculate:-
(A) Acceleration of the truck and the trailer.
(B) The tension in the connecting rope
Answer
192.9k+ views
Hint: Use the formula of newton’s second law of motion and substitute the parameters of both truck and trailer to calculate the acceleration of the truck and the trailer. Then in order to calculate the tension in the connecting rope, total force acting on the trailer is considered.
Useful formula:
By the newton’s second law of motion
$F = ma$
Where $F$ is the total force on the truck, $m$ is the mass of the truck and trailer and $a$ is the acceleration of the truck and the trailer.
Complete step by step solution:
Given data from the question are
Mass of the truck, $M = 1000\,Kg$
Mass of the trailer, $m = 2000\,Kg$
Frictional force on the truck, ${F_T} = 500\,N$
Frictional force on the trailer,${F_t} = 1000\,N$
Total force on the truck, $F = 6000\,N$
(A) By considering the formula of newton’s second law,
$F = ma$
mass is taken as the sum of the mass of truck and trailer
$F = \left( {M + m} \right)a$
Substituting the values of masses and force in the above equation.
$6000 - \left( {500 + 1000} \right) = \left( {1000 + 2000} \right)a$
In the above equation, frictional force is subtracted from the total force. This is because some force is lost through friction.
$6000 - 1500 = 3000a$
$4500 = 3000a$
By further simplification,
$a = 1.5\,m{s^{ - 1}}$.
Thus the acceleration of truck and trailer is obtained as $1.5\,m{s^{ - 1}}$.
(B) Let us consider that T be the tension of the connecting rope that connects the truck and the trailer.
Tension in the rope is the sum of the force acting on the trailer and the frictional force acting on it.
$T = {F_t} + force\,on\,trailer$
$T = 1000 + 2000a$
$T = \left( {2000 \times 1.5} \right) + 1000$
By doing arithmetic operation in the above equation,
$T = 4000\,N$
Tension in the connecting rope is obtained as $4000\,N$
Note: For calculating the tension acting on the rope that connects the truck and the trailer, only the total force that acts on the trailer is considered. This is because tension is the horizontal force , and this force in the rope is mainly given by the trailer as it is pulled by it.
Useful formula:
By the newton’s second law of motion
$F = ma$
Where $F$ is the total force on the truck, $m$ is the mass of the truck and trailer and $a$ is the acceleration of the truck and the trailer.
Complete step by step solution:
Given data from the question are
Mass of the truck, $M = 1000\,Kg$
Mass of the trailer, $m = 2000\,Kg$
Frictional force on the truck, ${F_T} = 500\,N$
Frictional force on the trailer,${F_t} = 1000\,N$
Total force on the truck, $F = 6000\,N$

(A) By considering the formula of newton’s second law,
$F = ma$
mass is taken as the sum of the mass of truck and trailer
$F = \left( {M + m} \right)a$
Substituting the values of masses and force in the above equation.
$6000 - \left( {500 + 1000} \right) = \left( {1000 + 2000} \right)a$
In the above equation, frictional force is subtracted from the total force. This is because some force is lost through friction.
$6000 - 1500 = 3000a$
$4500 = 3000a$
By further simplification,
$a = 1.5\,m{s^{ - 1}}$.
Thus the acceleration of truck and trailer is obtained as $1.5\,m{s^{ - 1}}$.
(B) Let us consider that T be the tension of the connecting rope that connects the truck and the trailer.
Tension in the rope is the sum of the force acting on the trailer and the frictional force acting on it.
$T = {F_t} + force\,on\,trailer$
$T = 1000 + 2000a$
$T = \left( {2000 \times 1.5} \right) + 1000$
By doing arithmetic operation in the above equation,
$T = 4000\,N$
Tension in the connecting rope is obtained as $4000\,N$
Note: For calculating the tension acting on the rope that connects the truck and the trailer, only the total force that acts on the trailer is considered. This is because tension is the horizontal force , and this force in the rope is mainly given by the trailer as it is pulled by it.
Recently Updated Pages
Electrical Resistance - Important Concepts and Tips for JEE

JEE Main Login 2026 - Step-by-Step Explanation

Average Atomic Mass - Important Concepts and Tips for JEE

Hydrogen and Its Type Important Concepts and Tips for JEE Exam Preparation

How to find Oxidation Number - Important Concepts for JEE

JEE Main 2023 (February 1st Shift 1) Maths Question Paper with Answer Key

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Hybridisation in Chemistry – Concept, Types & Applications

Equation of Trajectory in Projectile Motion: Derivation & Proof

Atomic Structure: Definition, Models, and Examples

Angle of Deviation in a Prism – Formula, Diagram & Applications

Other Pages
NCERT Solutions For Class 11 Physics Chapter 2 Motion In A Straight Line - 2025-26

NCERT Solutions For Class 11 Physics Chapter 1 Units and Measurements - 2025-26

NCERT Solutions For Class 11 Physics Chapter 3 Motion In A Plane - 2025-26

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions For Class 11 Physics Chapter 5 Work Energy And Power - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




