
A proton of mass \[1.67 \times {10^{ - 27}}\;kg\] and charge \[1.68 \times {10^{ - 19}}\;C\] is projected with a speed of \[2 \times {10^6}m/s\;\]at an angle of \[{60^o}\]to the \[X\]−axis. If a uniform magnetic field of \[0.10\;T\] is applied along \[Y\]−axis, the path of the proton is
A. a circle of radius \[0.2m\] and time period \[\pi \times {10^{ - 7}}\;s\]
B. a circle of radius \[0.1m\] and time period \[2\pi \times {10^{ - 7}}\;s\]
C. a helix of radius \[0.1m\] and time period \[2\pi \times {10^{ - 7}}\;s\]
D. a helix of radius \[0.2m\] and time period \[4\pi \times {10^{ - 7}}\;s\]
Answer
146.7k+ views
Hint: In the given question, we need to determine the path of a proton. That means we need to find the radius of the circular path and the time period of the particle moving along a circular path. For this, we need to use the following formulae for radius and time period to get the desired result.
Formula used:
The following formulae are used to solve the given question.
The radius of circular path of charged particle is \[r = \dfrac{{mv\sin \theta }}{{qB}}\].
Here, \[r\] indicates the radius of curvature of the path of a charged particle with mass \[m\] as well as charge \[q\] travelling at a speed \[v\] perpendicular to a magnetic field of intensity \[B\].
Also, the time period is \[T = \dfrac{{2\pi m}}{{qB}}\]
Here, \[T\] is the time period.
Complete answer:
Consider the following figure.
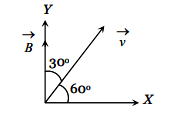
Image: Angle between magnetic field of intensity and velocity
We know that the radius of circular path of charged particle is \[r = \dfrac{{mv\sin \theta }}{{qB}}\]
But \[m = 1.67 \times {10^{ - 27}}\;kg,v = 2 \times {10^6}m/s\;,q = 1.68 \times {10^{ - 19}}\;C,\theta = {30^o},\] and \[B = 0.10\;T\]
This gives, \[r = \dfrac{{1.67 \times {{10}^{ - 27}}\; \times 2 \times {{10}^6} \times \sin {{30}^o}}}{{1.68 \times {{10}^{ - 19}} \times 0.10}}\]
By simplifying, we get
\[r = 0.1{\rm{ }}m\]
Also, the time period is given by
\[T = \dfrac{{2\pi m}}{{qB}}\]
But \[m = 1.67 \times {10^{ - 27}}\;kg\;,q = 1.68 \times {10^{ - 19}}\;C,\] and \[B = 0.10\;T\]
So, we get \[T = \dfrac{{2\pi \times 1.67 \times {{10}^{ - 27}}}}{{1.68 \times {{10}^{ - 19}} \times 0.10}}\]
By solving, we get
\[T = 2\pi \times {10^{ - 7}}{\rm{ S}}\]
Hence, the path of proton is a circular of radius \[0.1{\rm{ }}m\] and time period \[2\pi \times {10^{ - 7}}\;s\].
Therefore, the correct option is (B).
Note:Many students make mistake in simplification part. That means, they may get wrong while calculating the power of ten. Also, it is necessary to use diagrammatic representation to illustrate the given condition.
Formula used:
The following formulae are used to solve the given question.
The radius of circular path of charged particle is \[r = \dfrac{{mv\sin \theta }}{{qB}}\].
Here, \[r\] indicates the radius of curvature of the path of a charged particle with mass \[m\] as well as charge \[q\] travelling at a speed \[v\] perpendicular to a magnetic field of intensity \[B\].
Also, the time period is \[T = \dfrac{{2\pi m}}{{qB}}\]
Here, \[T\] is the time period.
Complete answer:
Consider the following figure.

Image: Angle between magnetic field of intensity and velocity
We know that the radius of circular path of charged particle is \[r = \dfrac{{mv\sin \theta }}{{qB}}\]
But \[m = 1.67 \times {10^{ - 27}}\;kg,v = 2 \times {10^6}m/s\;,q = 1.68 \times {10^{ - 19}}\;C,\theta = {30^o},\] and \[B = 0.10\;T\]
This gives, \[r = \dfrac{{1.67 \times {{10}^{ - 27}}\; \times 2 \times {{10}^6} \times \sin {{30}^o}}}{{1.68 \times {{10}^{ - 19}} \times 0.10}}\]
By simplifying, we get
\[r = 0.1{\rm{ }}m\]
Also, the time period is given by
\[T = \dfrac{{2\pi m}}{{qB}}\]
But \[m = 1.67 \times {10^{ - 27}}\;kg\;,q = 1.68 \times {10^{ - 19}}\;C,\] and \[B = 0.10\;T\]
So, we get \[T = \dfrac{{2\pi \times 1.67 \times {{10}^{ - 27}}}}{{1.68 \times {{10}^{ - 19}} \times 0.10}}\]
By solving, we get
\[T = 2\pi \times {10^{ - 7}}{\rm{ S}}\]
Hence, the path of proton is a circular of radius \[0.1{\rm{ }}m\] and time period \[2\pi \times {10^{ - 7}}\;s\].
Therefore, the correct option is (B).
Note:Many students make mistake in simplification part. That means, they may get wrong while calculating the power of ten. Also, it is necessary to use diagrammatic representation to illustrate the given condition.
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Ideal and Non-Ideal Solutions Raoult's Law - JEE

A proton accelerated by a potential difference of 500 class 12 physics JEE_Main

Electrical Field of Charged Spherical Shell - JEE

Other Pages
Formula for number of images formed by two plane mirrors class 12 physics JEE_Main

Charging and Discharging of Capacitor

JEE Advanced Study Plan for 2025: Tips, Timetable, and Strategy

Collision - Important Concepts and Tips for JEE

JEE Main Chemistry Question Paper with Answer Keys and Solutions

If a wire of resistance R is stretched to double of class 12 physics JEE_Main




