
A particle moves through angular displacement $\theta $ on a circular path of radius r. The linear displacement will be:
A) $2r\sin \left( {\dfrac{\theta }{2}} \right)$.
B) $2r\cos \left( {\dfrac{\theta }{2}} \right)$.
C) $2r\tan \left( {\dfrac{\theta }{2}} \right)$.
D) $2r\cot \left( {\dfrac{\theta }{2}} \right)$.
Answer
180k+ views
Hint: A displacement is defined as the shortest distance between the intimal and final position. The angular displacement is the displacement on the circular track which is represented by angle which is$\theta $ whereas linear displacement will be the shortest distance between the initial and the final point on the circular point.
Formula Used: The formula for the linear displacement is given by,
$ \Rightarrow \Delta \vec r = \sqrt {{r_2}^2 + {r_1}^2 - 2{r_1}{r_2}\cos \theta } $
Complete step by step answer:
It is given in the problem that a particle moves through angular displacement $\theta $ on a circular path of radius r and we need to find the linear displacement between the initial and the final position of the body.
As it is given that the angle between the initial and final position or the angular displacement is given to be$\theta $. Let the initial position vector be ${\vec r_1}$ and the final position vector is ${\vec r_2}$ and the points on the circle be A and B respectively.
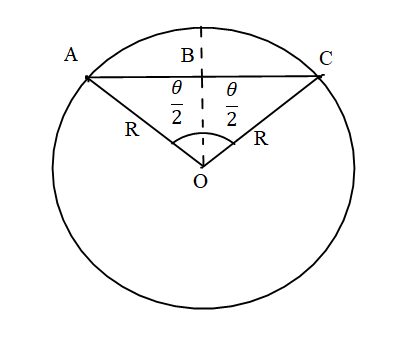
Here the linear displacement is equal to AC. Let us calculate the value of AC from both of the triangle ABO and triangle BCO.
In triangle ABO,
$ \Rightarrow \sin \left( {\dfrac{\theta }{2}} \right) = \dfrac{{AB}}{R}$
$ \Rightarrow AB = R\sin \left( {\dfrac{\theta }{2}} \right)$………eq. (1)
In triangle BCO,
$ \Rightarrow \sin \left( {\dfrac{\theta }{2}} \right) = \dfrac{{BC}}{R}$
$ \Rightarrow BC = R\sin \left( {\dfrac{\theta }{2}} \right)$………eq. (2)
Since, $AC = AB + BC$.
Replacing the values of AB and BC from the equation (1) and equation (2) in the above equation.
$ \Rightarrow AC = AB + BC$
\[ \Rightarrow AC = \left[ {R\sin \left( {\dfrac{\theta }{2}} \right)} \right] + \left[ {R\sin \left( {\dfrac{\theta }{2}} \right)} \right]\]
\[ \Rightarrow AC = 2 \cdot R\sin \left( {\dfrac{\theta }{2}} \right)\].
The linear displacement will be equal to\[AC = 2 \cdot R\sin \left( {\dfrac{\theta }{2}} \right)\]. The correct answer is option A.
Note: It is advisable to the students to understand and remember the formula of the vector addition or subtraction as it can help in solving these kinds of problems. The angle $\theta $ is between the line joining the initial and the final position with the center of the circle.
Formula Used: The formula for the linear displacement is given by,
$ \Rightarrow \Delta \vec r = \sqrt {{r_2}^2 + {r_1}^2 - 2{r_1}{r_2}\cos \theta } $
Complete step by step answer:
It is given in the problem that a particle moves through angular displacement $\theta $ on a circular path of radius r and we need to find the linear displacement between the initial and the final position of the body.
As it is given that the angle between the initial and final position or the angular displacement is given to be$\theta $. Let the initial position vector be ${\vec r_1}$ and the final position vector is ${\vec r_2}$ and the points on the circle be A and B respectively.

Here the linear displacement is equal to AC. Let us calculate the value of AC from both of the triangle ABO and triangle BCO.
In triangle ABO,
$ \Rightarrow \sin \left( {\dfrac{\theta }{2}} \right) = \dfrac{{AB}}{R}$
$ \Rightarrow AB = R\sin \left( {\dfrac{\theta }{2}} \right)$………eq. (1)
In triangle BCO,
$ \Rightarrow \sin \left( {\dfrac{\theta }{2}} \right) = \dfrac{{BC}}{R}$
$ \Rightarrow BC = R\sin \left( {\dfrac{\theta }{2}} \right)$………eq. (2)
Since, $AC = AB + BC$.
Replacing the values of AB and BC from the equation (1) and equation (2) in the above equation.
$ \Rightarrow AC = AB + BC$
\[ \Rightarrow AC = \left[ {R\sin \left( {\dfrac{\theta }{2}} \right)} \right] + \left[ {R\sin \left( {\dfrac{\theta }{2}} \right)} \right]\]
\[ \Rightarrow AC = 2 \cdot R\sin \left( {\dfrac{\theta }{2}} \right)\].
The linear displacement will be equal to\[AC = 2 \cdot R\sin \left( {\dfrac{\theta }{2}} \right)\]. The correct answer is option A.
Note: It is advisable to the students to understand and remember the formula of the vector addition or subtraction as it can help in solving these kinds of problems. The angle $\theta $ is between the line joining the initial and the final position with the center of the circle.
Recently Updated Pages
JEE Electricity and Magnetism Important Concepts and Tips for Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

States of Matter Chapter For JEE Main Chemistry

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Displacement-Time Graph and Velocity-Time Graph for JEE

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

What is Hybridisation in Chemistry?

Other Pages
NCERT Solutions For Class 11 Physics Chapter 2 Motion In A Straight Line - 2025-26

NCERT Solutions For Class 11 Physics Chapter 1 Units and Measurements - 2025-26

NCERT Solutions For Class 11 Physics Chapter 3 Motion In A Plane - 2025-26

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26




