
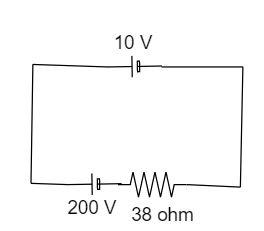
A 10 V cell of negligible internal resistance is connected in parallel across a battery of emf $200\,V$ and internal resistance $38\,\Omega $ as shown in the figure. Find the value of current in the circuit.
Answer
174.3k+ views
Hint: Find the value of the total net electro motive force by subtracting the value of the negligible resistance from the total emf of the battery. Substitute the obtained emf value in the rearranged ohm’s formula to find the value of the current flowing through the circuit.
Useful formula:
The ohm’s law is given by
$V = IR$
Where $V$ is the potential difference if the emf across the circuit, $I$ is the current in the circuit and the $R$ is the resistance in the circuit.
Complete step by step solution:
It is given that the
Internal resistance of the circuit, $r = 10\,V$
The emf across the battery, ${r_e} = 200\,V$
The net resistance of the circuit, $R = 38\,\Omega $
The net emf in the circuit is calculated by subtracting the negligible internal resistance from the total emf of the circuit.
$E = {r_e} - r$
Substituting the values in the above equation
$E = 200 - 10$
Subtracting the values in the right hand side.
$E = 190\,V$
Substituting the value of the emf in the ohm’s law.
$V = IR$
By rearranging the above formula,
$I = \dfrac{V}{R}$
Substituting the values of the resistance in the emf in the above step.
$I = \dfrac{{190}}{{38}}$
By doing the simple division in the above step.
$I = 5\,A$
The value of the current in the given circuit is $5\,A$.
Note: The electromotive force is the energy per unit charge that is produced from either battery or the generator. In the battery, the energy is converted from one form to the other. The internal resistance in the battery itself, because of the heating of its own parts.
Useful formula:
The ohm’s law is given by
$V = IR$
Where $V$ is the potential difference if the emf across the circuit, $I$ is the current in the circuit and the $R$ is the resistance in the circuit.
Complete step by step solution:
It is given that the
Internal resistance of the circuit, $r = 10\,V$
The emf across the battery, ${r_e} = 200\,V$
The net resistance of the circuit, $R = 38\,\Omega $
The net emf in the circuit is calculated by subtracting the negligible internal resistance from the total emf of the circuit.
$E = {r_e} - r$
Substituting the values in the above equation
$E = 200 - 10$
Subtracting the values in the right hand side.
$E = 190\,V$
Substituting the value of the emf in the ohm’s law.
$V = IR$
By rearranging the above formula,
$I = \dfrac{V}{R}$
Substituting the values of the resistance in the emf in the above step.
$I = \dfrac{{190}}{{38}}$
By doing the simple division in the above step.
$I = 5\,A$
The value of the current in the given circuit is $5\,A$.
Note: The electromotive force is the energy per unit charge that is produced from either battery or the generator. In the battery, the energy is converted from one form to the other. The internal resistance in the battery itself, because of the heating of its own parts.
Recently Updated Pages
JEE Main 2025-26 Atoms and Nuclei Mock Test: Free Practice Online

JEE Main 2025-26: Dual Nature of Matter and Radiation Mock Test

JEE Main 2025-26 Electronic Devices Mock Test – Free Practice

JEE Main Mock Test 2025-26: Experimental Skills Chapter Online Practice

JEE Main 2025-26 Current Electricity Mock Test: Free Practice Online

JEE Main 2025-26 Rotational Motion Mock Test – Free Practice Online

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Displacement-Time Graph and Velocity-Time Graph for JEE

Uniform Acceleration

Electric field due to uniformly charged sphere class 12 physics JEE_Main

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Instantaneous Velocity - Formula based Examples for JEE

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Essential Derivations for CBSE Class 12 Physics: Stepwise & PDF Solutions

Electron Gain Enthalpy and Electron Affinity for JEE

What is Hybridisation in Chemistry?




