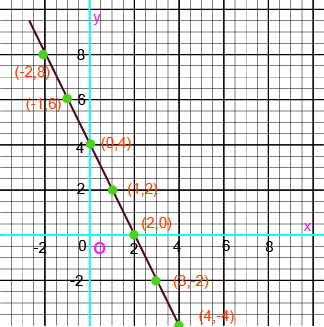
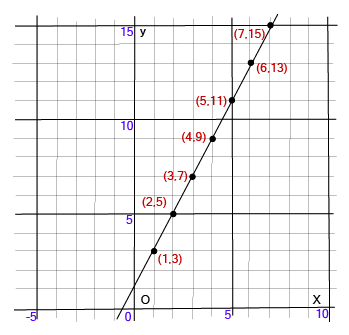
Coordinate Geometry Class 9 Important Questions with Answers PDF download
FAQs on CBSE Important Questions for Class 9 Maths Coordinate Geometry - 2025-26
1. What types of important questions are asked from Chapter 3, Coordinate Geometry, in the Class 9 exam for 2025-26?
For the 2025-26 session, important questions from Coordinate Geometry typically fall into these categories:
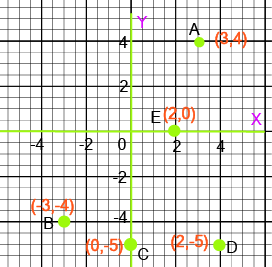
- 1-mark questions (MCQs/VSA): Identifying the quadrant of a point, finding the coordinates of a point on the x-axis or y-axis, or defining terms like abscissa and ordinate.
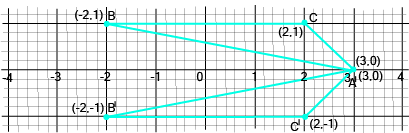
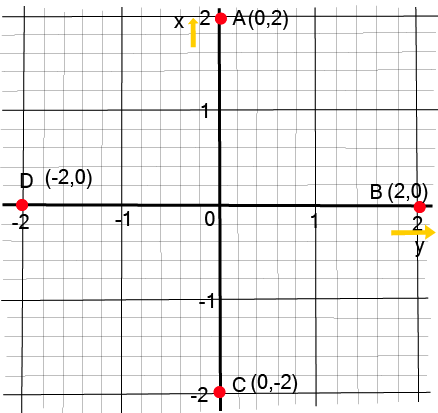
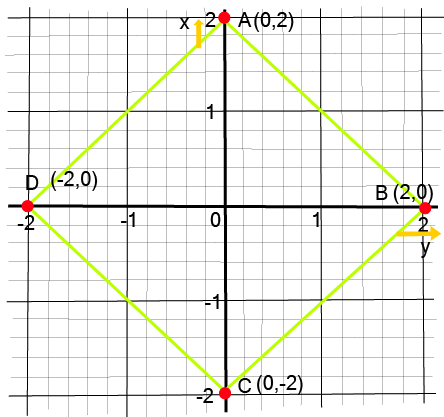
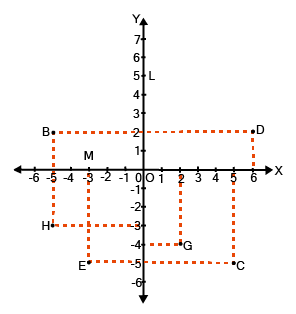
- 2/3-mark questions: Plotting given points on a Cartesian plane and identifying the geometric figure formed (e.g., triangle, square, rectangle).
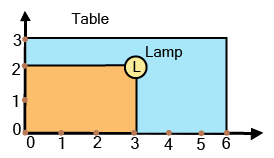
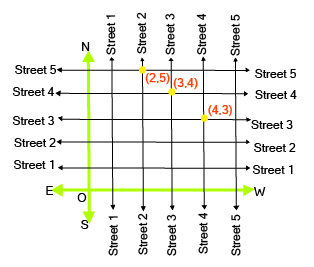
- Case-study questions: Applying coordinate geometry concepts to a real-world scenario, like a classroom seating plan or a map layout.
2. Which topics in Coordinate Geometry are most important for scoring marks in the Class 9 exam?
To score well, focus on these key areas:
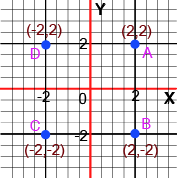
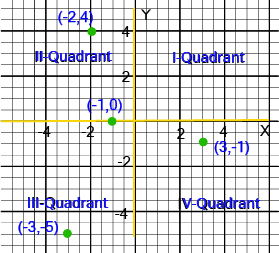
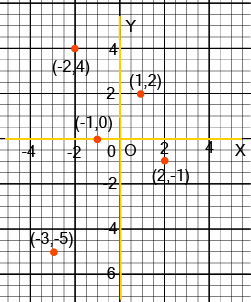
- Understanding Quadrants: Knowing the sign of the coordinates (x, y) in all four quadrants is crucial. For example, Quadrant I is (+,+), Quadrant II is (-,+), and so on.
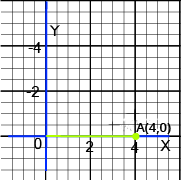
- Points on Axes: A point on the x-axis has coordinates (x, 0), and a point on the y-axis has coordinates (0, y). Many objective questions are based on this rule.
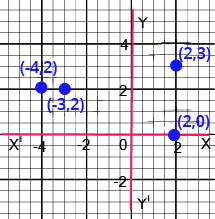
- Plotting Points: Accurately plotting points and interpreting their positions is essential for solving multi-mark questions.
3. How are case-study based important questions from Coordinate Geometry structured in the exam?
A case-study question typically presents a real-world situation on a grid, such as a map of a colony or a seating arrangement. You will be asked to:
- Determine the coordinates of specific locations or objects.
- Identify objects in a particular quadrant or on an axis.
- Describe the geometric relationship between different points.
4. What are some expected questions related to plotting points with specific conditions?
Important questions often involve plotting points that satisfy certain rules. For instance, you might be asked to plot:
- Three or four points and identify the resulting geometric shape (e.g., a triangle, rectangle, or rhombus).
- A point whose abscissa (x-coordinate) is negative and ordinate (y-coordinate) is positive.
- Points that are mirror images of each other with respect to the x-axis or y-axis.
5. Why is it important to understand the sign conventions for different quadrants? How does this help avoid exam mistakes?
Understanding sign conventions is critical because it allows you to instantly determine a point's location without plotting it, which saves time in exams, especially in MCQs. For example, knowing that any point in Quadrant III must have both a negative abscissa and a negative ordinate helps eliminate incorrect options quickly. This fundamental knowledge prevents common errors in questions that ask you to identify the quadrant for a point like (-5, -9).
6. What is the difference between an abscissa and an ordinate, and what kind of 1-mark questions can be expected from these terms?
The abscissa is the x-coordinate of a point, representing its perpendicular distance from the y-axis. The ordinate is the y-coordinate, representing its perpendicular distance from the x-axis. A typical 1-mark question might be: "For the point P(–4, 7), what is the value of the abscissa?" The answer is -4. These questions are designed to be quick but test your knowledge of fundamental terminology.
7. If a point's ordinate is zero, where must it lie? How can this concept be used in higher-mark questions?
If a point's ordinate (y-coordinate) is zero, it must lie on the x-axis. This is a crucial concept for solving multi-step problems. For example, an important question might ask you to find the vertices of a rectangle where one side lies on the x-axis. Knowing that all points on that side will have a y-coordinate of zero simplifies the problem significantly and helps in correctly plotting the shape.
8. What is a common mistake students make when identifying coordinates on the x-axis or y-axis?
A very common mistake is reversing the coordinates. Students often write (y, 0) for a point on the y-axis instead of the correct (0, y), or (0, x) for a point on the x-axis instead of (x, 0). To prevent this, always remember:
- On the x-axis, you move left or right, but not up or down. So, the y-coordinate is always zero.
- On the y-axis, you move up or down, but not left or right. So, the x-coordinate is always zero.

























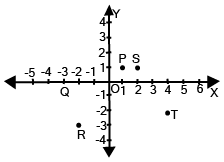
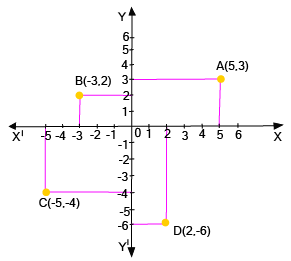
![\[{\bf{y}} = {\bf{x}}\]](https://www.vedantu.com/seo/content-images/1c42c8cc-ae85-4051-93ba-4a0e360840ce.png)