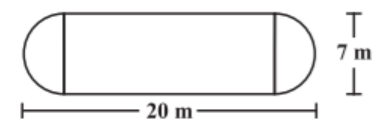
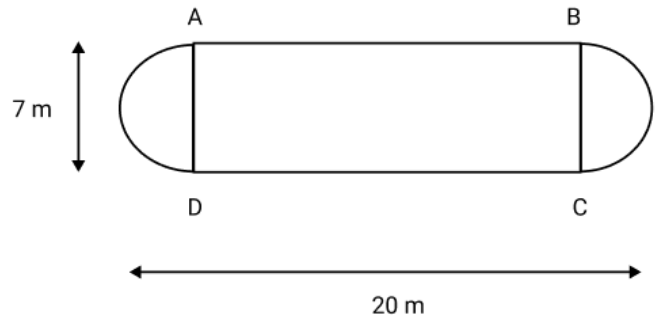
Class 8 Maths important questions with answers PDF download
FAQs on CBSE Important Questions for Class 8 Maths - 2025-26
1. Are these important questions for Class 8 Maths aligned with the latest CBSE syllabus for 2025-26?
Yes, all important questions are meticulously curated to be fully aligned with the latest CBSE syllabus and examination guidelines for the 2025-26 academic session. They cover every chapter prescribed by the NCERT, ensuring your preparation is comprehensive and targeted.
2. How do these important questions help in scoring well in the final exam?
These questions are selected based on their probability of appearing in the exam and their conceptual importance. They help by:
- Focusing on topics with higher marks weightage as per the exam pattern.
- Including frequently asked questions from past papers to reveal trends.
- Providing practice on various question types, from 1-mark objective to 5-mark long-answer questions.
- Building confidence by familiarising you with the actual exam format and difficulty level.
3. What is the best strategy to use these important questions for effective revision?
For maximum benefit, first, thoroughly revise the concepts of a chapter from your textbook. Then, attempt to solve the important questions for that chapter as if you are in a test. Finally, analyse your answers and mistakes to identify your weak areas. This practice helps improve speed, accuracy, and time management skills for the actual exam.
4. Do these important questions include Higher Order Thinking Skills (HOTS) problems?
Yes, this collection includes a balanced mix of question types, including Higher Order Thinking Skills (HOTS) problems. These questions are designed to challenge your conceptual understanding and problem-solving abilities beyond direct formula application, preparing you for the trickier problems in the exam.
5. How does practising these questions offer an advantage over only solving NCERT textbook exercises?
While NCERT exercises build a strong foundation, important questions provide an exam-oriented perspective. They often integrate concepts from different parts of a chapter or multiple chapters, mirroring the complexity of board exam questions. This helps you transition from basic understanding to strategic application of knowledge under exam conditions.
6. Which chapters in Class 8 Maths should I focus on more while using these important questions?
While every chapter is essential, topics like Algebraic Expressions and Identities, Mensuration, Squares and Square Roots, and Comparing Quantities often carry significant weightage. It is advisable to dedicate extra practice to the important questions from these high-value chapters to maximise your score.
7. What are some common mistakes students make in high-weightage topics that these questions help to address?
In chapters like Mensuration, students often confuse formulas for different shapes. In Algebra, sign errors are common. These important questions include problems designed to specifically test these common trap points. By practising them, you can proactively identify and rectify these potential error-prone areas before the exam.
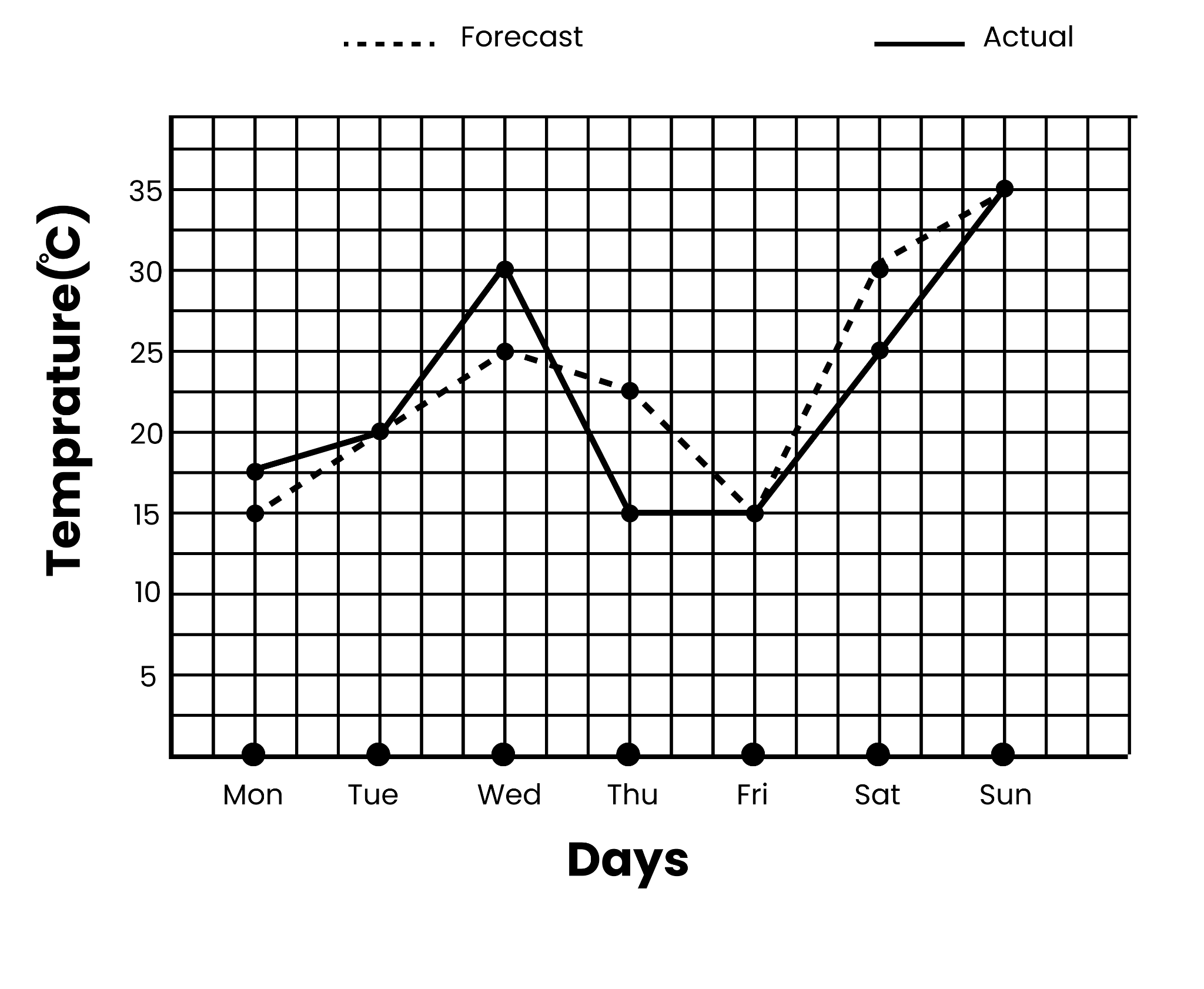
8. Why is it important to practise questions from topics that seem easy, like 'Data Handling' or 'Introduction to Graphs'?
These topics are crucial for developing analytical and interpretation skills. Questions from these chapters often test your ability to read data, draw conclusions, and represent information visually. The important questions ensure you master the application and interpretation aspects of these topics, which are essential for scoring full marks and building a strong foundation for higher classes.