CBSE Important Questions for Class 11 Maths Trigonometric Functions - 2025-26

1 Mark Questions

1. Find the radian measure corresponding to  $ 5{}^\circ \text{ }37'\text{ }30'' $  

Ans- 

Converting the given value to a pure degree form

 $ {{5}^{\circ }}37'30''={{5}^{\circ }}37'\left( \dfrac{30}{60} \right)' $ 

 $ \Rightarrow {{5}^{\circ }}37'60''={{5}^{\circ }}\left( \dfrac{75}{2} \right)' $ 

 $ \Rightarrow {{5}^{\circ }}37'60''={{5}^{\circ }}{{\left( \dfrac{75}{2\left( 60 \right)} \right)}^{\circ }} $ 

 $ \Rightarrow {{5}^{\circ }}37'60''={{\left( \dfrac{45}{8} \right)}^{\circ }} $ 

Degree to Radian Conversion

 $ \left( \dfrac{45}{8} \right)\left( \dfrac{\pi }{180} \right)=\dfrac{\pi }{32}\text{rad} $ 

2. Find degree measure corresponding to  $ {{\left( \dfrac{\pi }{16} \right)}^{c}} $  

Ans- 

Converting the given value from radian to degree form

$ \dfrac{\pi }{16}\times \dfrac{180}{\pi }={{\left( \dfrac{45}{4} \right)}^{\circ }} $ 

Simplify degree form

$ {{\left( \dfrac{45}{4} \right)}^{\circ }}={{11}^{\circ }}15' $ 

3. Find the length of an arc of a circle of radius  $ 5cm $  subtending a central angle measuring  $ 15{}^\circ  $  

Ans- 

The arc of a circle with a radius of  $ 5\,\text{cm} $  with a central angle of  $ {{15}^{\circ }} $  should be of the length  $ \dfrac{5\pi }{12}cm $  using the formula  $ \text{Arc}\,\text{=}\,\pi \times \left( \theta  \right) $ .

4. Find the value of  $ \dfrac{19\pi }{3} $  

Ans- 

We have  $ \tan \dfrac{19\pi }{3} $ 

 $ \tan \dfrac{19\pi }{3}=\tan \left( 6\dfrac{\pi }{3} \right) $ 

                   $ =\tan \left( 6\pi +\dfrac{\pi }{3} \right) $ 

                   $ =\tan \left( 3\times 2\pi +\dfrac{\pi }{3} \right) $ 

                   $ =\tan \left( \dfrac{\pi }{3} \right) $ 

                   $ =\sqrt{3} $ 

5. Find the value of  $ \sin \left( -1125{}^\circ  \right) $  

Ans- 

We have  $ \sin \left( -{{1125}^{\circ }} \right) $ 

 $ \sin \left( -\dfrac{1125}{360}\times {{360}^{\circ }} \right) $ 

 $ =-\sin \left( \left( 3+\dfrac{45}{360} \right)\times {{360}^{\circ }} \right) $ 

 $ =-\sin \left( {{45}^{\circ }} \right) $ 

 $ =-\dfrac{1}{\sqrt{2}} $ 

6. Find the value of  $ \tan \left( {{15}^{\circ }} \right) $  

Ans- 

We have  $ \tan {{15}^{\circ }} $ 

 $ \tan {{15}^{\circ }}=\tan \left( {{60}^{\circ }}-{{45}^{\circ }} \right) $ 

                 $ =\dfrac{\tan {{60}^{\circ }}-\tan {{45}^{\circ }}}{1+\tan {{60}^{\circ }}\times \tan {{45}^{\circ }}} $ 

                 $ =\dfrac{\sqrt{3}-1}{\sqrt{3}+1} $ 

7. If  $ \sin A=\dfrac{3}{5} $  and  $ \dfrac{\pi }{2}<A< $  find $ \cos A $  

Ans- 

The condition  $ \dfrac{\pi }{2}<A $  denotes that we need to take into account for the second quadrant, hence the cosine value will be negative. 

Therefore, 

 $ \cos A=\dfrac{-4}{5} $ 

8. If  $ \tan A=\dfrac{a}{a+1} $  and  $ \tan B=\dfrac{1}{2a+1} $  then find the value of  $ A+B $  

Ans- 

 $ \tan \left( A+B \right)=\dfrac{\tan A+\tan B}{1-\tan A\tan B} $ 

                           $ =\dfrac{\dfrac{a}{a+1}+\dfrac{1}{2a+1}}{1-\dfrac{a}{a+1}\cdot \dfrac{1}{2a+1}} $ 

                          $ =\dfrac{\dfrac{2{{a}^{2}}+2a+1}{\left( a+1 \right)\left( 2a+1 \right)}}{\dfrac{\left( a+1 \right)\left( 2a+1 \right)-a}{\left( a+1 \right)\left( 2a+1 \right)}} $ 

                          $ =1 $ 

Which can only be possible if  $ A+B={{45}^{\circ }} $ .

9. Express  $ \sin 12\theta +\sin 4\theta  $  as the product of sines and cosine

Ans-

Using the trigonometric difference formula, we get

 $ \sin 12\theta +\sin 4\theta =\sin \left( 8\theta +4\theta  \right)+\sin \left( 8\theta -4\theta  \right) $  

                                    $ =2\sin 8\theta \cos 4\theta  $ 

10. Express  $ 2\cos 4x\sin 2x $  as an algebraic sum of sines or cosine.

Ans- 

 $ 2\cos 4x\sin 2x=\sin \left( 2x+4x \right)+\sin \left( 2x-4x \right) $ 

                                 $ =\sin 6x+\sin \left( -2x \right) $ 

                                  $ =\sin 6x-\sin 2x $ 

11. Write the range of  $ \cos \theta  $  

Ans- 

The cosine function is a periodic function with a domain of  $ \mathbb{R} $  and a range of  $ \left[ -1,1 \right] $ .

12. What is domain of  $ \sec \theta  $  

Ans- 

The secant function is the reciprocal of the cosine function, it has a domain of  $ \mathbb{R}-\left\{ (2n+1)\dfrac{\pi }{2};n\in \mathbb{Z} \right\} $  because those are the points where the cosine function equates to  $ 0 $ .

13. Find the principal solution of  $ \cot x=3 $  

Ans- 

The principal solution of  $ \cot x=3 $  is for the following input values  $ x=\dfrac{5\pi }{6},\dfrac{11\pi }{6} $ .

14. Write the general solution of  $ \cos \theta =0 $  

Ans- 

The general solution for the equation  $ \cos \theta =0 $  is  $ \theta =(2n+1)\dfrac{\pi }{2},n\in \mathbb{Z} $ .

15. If  $ \sin x=\dfrac{\sqrt{5}}{3} $ and  $ 0\text{ }<\text{ }x\text{ }<\dfrac{\pi }{2} $ find the value of $ \cos 2x $  

Ans- 

We know that  $ \cos 2x=1-{{\sin }^{2}}x $ 

 $ \cos 2x=1-2{{\left( \dfrac{\sqrt{5}}{3} \right)}^{2}} $ 

                $ =1-2\times \dfrac{5}{9} $ 

                $ =-\dfrac{1}{9} $ 

16. If  $ \cos x=-\dfrac{1}{3} $  and  $ x $  lies in quadrant  $ \text{III} $ , find the value of  $ \sin \dfrac{x}{2} $  

Ans- 

We know that  $ \cos 2x=1-2{{\sin }^{2}}x $ 

 $ \cos \left( 2\left( \dfrac{x}{2} \right) \right)=1-2{{\sin }^{2}}\left( \dfrac{x}{2} \right) $ 

 $ \Rightarrow -\dfrac{1}{3}=1-2{{\sin }^{2}}\dfrac{x}{2} $ 

 $ \Rightarrow 2{{\sin }^{2}}\dfrac{x}{2}=1+\dfrac{1}{3} $ 

 $ \Rightarrow {{\sin }^{2}}\dfrac{x}{2}=\dfrac{2}{3} $ 

 $ \Rightarrow \sin \dfrac{x}{2}=\pm \sqrt{\dfrac{2}{3}} $ 

 $ \Rightarrow \sin \dfrac{x}{2}=\sqrt{\dfrac{2}{3}}\,\,\,\,\,\left[ \text{2nd Quadrant} \right] $ 

17. Convert into radian measures  $ -47{}^\circ 30' $  

Ans- 

Convert into pure degree form and then convert to radian

 $ -47{}^\circ 30'=-{{\left( 47+\dfrac{30}{60} \right)}^{{}^\circ }} $ 

                   $ =-{{\left( 47+\dfrac{1}{2} \right)}^{{}^\circ }} $ 

                   $ =-\left( \dfrac{95}{2}\times \dfrac{\pi }{180} \right)\text{rad} $ 

                   $ =-\dfrac{19\pi }{72}\text{rad} $ 

18. Evaluate  $ \tan 75{}^\circ  $  

Ans- 

Use the trigonometric addition formula for the tangent function

 $ \tan {{75}^{\circ }}=\tan ({{45}^{\circ }}+{{30}^{\circ }}) $ 

                 $ =\dfrac{\tan {{45}^{\circ }}+\tan {{30}^{\circ }}}{1-\tan {{45}^{\circ }}\tan {{30}^{\circ }}} $ 

                 $ =\dfrac{\sqrt{3}+1}{\sqrt{3}-1} $ 

19. Prove that  $ \sin (40+\theta )\cdot \cos (10+\theta )-\cos (40+\theta )\cdot \sin (10+\theta )=\dfrac{1}{2} $  

Ans-  

Let us take the left-hand side of the equation and make some manipulations.

We know,  $ \sin \left( a-b \right)=\sin a\cos b-\cos a\sin b $ 

 $ \text{L}\text{.H}\text{.S}=\sin (40+\theta )\cos (10+\theta )-\cos (40+\theta )\sin (10+\theta ) $ 

              $ =\sin \left[ 40+\theta -10-\theta  \right]=\sin 30 $ 

              $ =\dfrac{1}{2} $ 

20. Find the principal solution of the eq.  $ \sin x=\dfrac{\sqrt{3}}{2} $  

Ans- 

The principal solution of  $ \sin x=\dfrac{\sqrt{3}}{2} $  is the input values of  $ x=\dfrac{\pi }{3},\dfrac{2\pi }{3} $ 

21. Prove that  $ \cos \left( \dfrac{\pi }{4}+x \right)+\cos \left( \dfrac{\pi }{4}-x \right)=\sqrt{2}\cos x $ 

Ans- 

Let us start with the left-hand side and use the trigonometric differences formula for the cosine function

 $ \text{L}\text{.H}\text{.S}=\cos \left( \dfrac{\pi }{4}+x \right)+\cos \left( \dfrac{\pi }{4}-x \right) $ 

               $ =2\cos \dfrac{\pi }{4}\cos x $ 

               $ =2\left( \dfrac{1}{\sqrt{2}} \right)\cos x $ 

               $ =\sqrt{2}\cos x $ 

               $ =\text{R}\text{.H}\text{.S} $ 

22. Convert into radian measures  $ -37{}^\circ 30' $  

Ans- 

Convert into pure degree form and then convert from degree to radian

 $ -37{}^\circ 30'={{\left( 37+\dfrac{30}{60} \right)}^{{}^\circ }} $ 

                 $ =-{{\left( \dfrac{75}{2} \right)}^{{}^\circ }} $ 

                 $ =-\dfrac{75}{2}\times \dfrac{\pi }{180}\text{rad} $ 

                 $ =-\dfrac{5\pi }{24}\text{rad} $ 

23. Prove

 $ Sin\text{ }\left( n+1 \right)\text{ }x\text{ }Sin\text{ }\left( n+2 \right)\text{ }x\text{ }+\text{ }Cos\text{ }\left( n+1 \right)\text{ }x.\text{ }Cos\text{ }\left( n+2 \right)\text{ }x\text{ }=\text{ }Cos\text{ }x $   

Ans- 

 $ \text{L}\text{.H}\text{.S}\,\text{. = sin}\left( n+1 \right)x\sin \left( n+2 \right)x+\cos \left( n+1 \right)x\cos \left( n+2 \right)x $ 

                 $ =\cos \left\{ \left( n+1 \right)x-\left( n+2 \right)x \right\} $ 

                 $ =\cos \left( nx+x-n-2x \right) $ 

                 $ =\cos \left( -x \right) $ 

                 $ =\cos \left( x \right) $ 

24. Find the value of  $ \operatorname{Sin}\dfrac{31\pi }{3} $  

Ans- 

We have  $ \sin \dfrac{31\pi }{3} $ 

 $ \operatorname{Sin}\dfrac{31\pi }{3}=\operatorname{Sin}\left( 10\pi +\dfrac{\pi }{3} \right) $ 

                   $ =\operatorname{Sin}\left( 2\pi \times 5+\dfrac{\pi }{3} \right)\,\,\,\,\,\,\left[ \text{Periodic Function} \right] $ 

                   $ =\operatorname{Sin}\dfrac{\pi }{3} $ 

                   $ =\dfrac{\sqrt{3}}{2} $ 

25. Find the principal solution of the eq.  $ \tan x=-\dfrac{1}{\sqrt{3}} $ . 

Ans- 

The principal solution of the equation  $ \tan x=-\dfrac{1}{\sqrt{3}} $  will be the input values of  $ x=\dfrac{5\pi }{6},\dfrac{11\pi }{6} $ 

26. Convert into radian measures $ 5{}^\circ \text{ }37'\text{ }30'' $  

Ans- 

Converting the given value to a pure degree form

 $ {{5}^{\circ }}37'30''={{5}^{\circ }}37'\left( \dfrac{30}{60} \right)' $ 

 $ \Rightarrow {{5}^{\circ }}37'60''={{5}^{\circ }}\left( \dfrac{75}{2} \right)' $ 

 $ \Rightarrow {{5}^{\circ }}37'60''={{5}^{\circ }}{{\left( \dfrac{75}{2\left( 60 \right)} \right)}^{\circ }} $ 

 $ \Rightarrow {{5}^{\circ }}37'60''={{\left( \dfrac{45}{8} \right)}^{\circ }} $ 

Degree to Radian Conversion

 $ \left( \dfrac{45}{8} \right)\left( \dfrac{\pi }{180} \right)=\dfrac{\pi }{32}\text{rad} $ 

27.  Prove  $ Cos70{}^\circ .\text{ }Cos10{}^\circ +\text{ }Sin70{}^\circ .\text{ }Sin10{}^\circ =\dfrac{1}{2} $  

Ans- 

Starting with the left-hand side and using the trigonometric differences formula for the cosine function.

 $ \text{L}\text{.H}\text{.S}=\text{cos}\left( {{70}^{\circ }}{{10}^{\circ }} \right) $ 

               $ =\cos {{60}^{\circ }} $ 

               $ =\dfrac{1}{2} $ 

28.  Evaluate  $ 2\operatorname{Sin}\dfrac{\pi }{12} $  

Ans- 

Use the trigonometric difference formula for the sine function and expand

 $ 2\sin \dfrac{\pi }{12}=2\sin \left[ \dfrac{\pi }{4}-\dfrac{\pi }{6} \right] $ 

                   $ =2\left[ \sin \dfrac{\pi }{4}\cos \dfrac{\pi }{6}-\cos \dfrac{\pi }{4}\sin \dfrac{\pi }{6} \right] $ 

                   $ =2\left[ \dfrac{1}{\sqrt{2}}\times \dfrac{\sqrt{3}}{2}-\dfrac{1}{\sqrt{2}}\times \dfrac{1}{2} \right] $ 

                    $ =\dfrac{\sqrt{3}-1}{\sqrt{2}} $ 

29.  Find the solution of  $ \operatorname{Sin}x=-\dfrac{\sqrt{3}}{2} $  

Ans- 

We are required to find the general solution for the equation  $ \sin x=-\dfrac{\sqrt{3}}{2} $ 

 $ \operatorname{Sin}x=-\dfrac{\sqrt{3}}{2} $ 

 $ \Rightarrow \operatorname{Sin}x=\operatorname{Sin}\left( \pi +\dfrac{\pi }{3} \right) $ 

 $ \Rightarrow \operatorname{Sin}x=\operatorname{Sin}\dfrac{4\pi }{3} $ 

When

 $ \operatorname{Sin}\theta =\operatorname{Sin}\alpha  $ 

 $ \theta =n\pi +{{(-1)}^{n}}\cdot \alpha  $ 

 $ x=n\pi +{{(-1)}^{n}}\cdot \dfrac{4\pi }{3} $ 

30.  Prove that  $ \dfrac{\operatorname{Cos}9{}^\circ -\operatorname{Sin}9{}^\circ }{\operatorname{Cos}9{}^\circ +\operatorname{Sin}9{}^\circ }=\tan 36{}^\circ  $  

Ans- 

Let us start with the right-hand side and use the trigonometric differences formula for the tangent function.

 $ \text{R}\text{.H}\text{.S}=\tan 36{}^\circ  $ 

                $ =\tan \left( {{45}^{\circ }}-{{9}^{\circ }} \right) $ 

                $ =\dfrac{\tan {{45}^{\circ }}-\tan {{9}^{\circ }}}{1+\tan {{45}^{\circ }}\tan {{9}^{\circ }}} $ 

                $ =\dfrac{1-\tan {{9}^{\circ }}}{1+\tan {{9}^{\circ }}} $ 

                $ =\dfrac{\cos {{9}^{\circ }}-\sin {{9}^{\circ }}}{\cos {{9}^{\circ }}+\sin {{9}^{\circ }}} $ 

                $ =\text{L}\text{.H}\text{.S}\text{.} $ 

31.  Find the value of  $ \tan \dfrac{19\pi }{3} $  

Ans- 

We have  $ \tan \left( \dfrac{19\pi }{3} \right) $ 

 $ \tan \dfrac{19\pi }{3}=\tan \left( 6\pi -\dfrac{\pi }{3} \right) $ 

                  $ =\tan \left[ 3\times 2\pi +\dfrac{\pi }{3} \right]\,\,\,\,\,\,\,\,\,\,\left[ \text{Periodic Function} \right] $ 

                  $ =\tan \dfrac{\pi }{3} $ 

                  $ =\sqrt{3} $ 

32.  Prove  $ \operatorname{Cos}4x=1-8{{\operatorname{Sin}}^{2}}x.{{\operatorname{Cos}}^{2}}x $ 

Ans- 

Starting with the left-hand side and using the trigonometric addition formula, $ \cos 2x=1-2{{\sin }^{2}}x $ 

We get,

 $ \text{L}\text{.H}\text{.S}=\operatorname{Cos}4x $ 

               $ =1-2{{\operatorname{Sin}}^{2}}2x $ 

               $ =1-2{{(\operatorname{Sin}2x)}^{2}} $ 

               $ =1-2{{(2\operatorname{Sin}x.\operatorname{Cos}x)}^{2}} $ 

               $ =1-2(4{{\operatorname{Sin}}^{2}}x.{{\operatorname{Cos}}^{2}}x) $ 

               $ =1-8{{\operatorname{Sin}}^{2}}x.{{\operatorname{Cos}}^{2}}x $ 

33.  Prove  $ \dfrac{\operatorname{Cos}(\pi +x).\operatorname{Cos}(-x)}{\operatorname{Sin}(\pi -x).\operatorname{Cos}\left( \dfrac{\pi }{2}+x \right)}=Co{{t}^{2}}x $  

Ans- 

Starting with the left-hand side and using the trigonometric periodic identities, we obtain the following

 $ \text{L}\text{.H}\text{.S}\text{.}=\dfrac{\cos \left( \pi +x \right)\cos \left( -x \right)}{\sin \left( \pi -x \right)\cos \left( \dfrac{\pi }{2}+x \right)} $ 

                 $ =\dfrac{-\cos x\cos x}{-\sin x\sin x} $ 

                 $ ={{\cot }^{2}}x $ 

                 $ =\text{R}\text{.H}\text{.S}\text{.} $ 

34.  Prove that  $ \tan {{56}^{\circ }}=\dfrac{\operatorname{Cos}{{11}^{\circ }}+\operatorname{Sin}{{11}^{\circ }}}{\operatorname{Cos}{{11}^{\circ }}-\operatorname{Sin}{{11}^{\circ }}} $  

Ans- 

Starting with the left-hand side and using the trigonometric addition formula for the tangent function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\tan {{56}^{\circ }} $ 

                 $ =\tan ({{45}^{\circ }}+{{11}^{\circ }}) $ 

                 $ =\dfrac{\tan {{45}^{\circ }}+\tan {{11}^{\circ }}}{1-\tan {{45}^{\circ }}\cdot \tan {{11}^{\circ }}} $ 

                 $ =\dfrac{1+\tan {{11}^{\circ }}}{1-\tan {{11}^{\circ }}} $ 

                $ =\dfrac{\cos {{11}^{\circ }}+\sin {{11}^{\circ }}}{\cos {{11}^{\circ }}-\sin {{11}^{\circ }}} $ 

                $ =\text{R}\text{.H}\text{.S}\text{.} $ 

35.  Prove that  $ \operatorname{Cos}{{105}^{\circ }}+\operatorname{Cos}{{15}^{\circ }}=\operatorname{Sin}{{75}^{\circ }}-\operatorname{Sin}{{15}^{\circ }} $ 

Ans- 

Starting with the left-hand side and using the trigonometric difference formula for the cosine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\operatorname{Cos}{{105}^{\circ }}+\operatorname{Cos}{{15}^{\circ }} $ 

                 $ =\operatorname{Cos}({{90}^{\circ }}+{{15}^{\circ }})+\operatorname{Cos}({{90}^{\circ }}-{{75}^{\circ }}) $ 

                 $ =-\operatorname{Sin}{{15}^{\circ }}+\operatorname{Sin}{{75}^{\circ }} $ 

                 $ =\operatorname{Sin}{{75}^{\circ }}-\operatorname{Sin}{{15}^{\circ }} $ 

                 $ =\text{R}\text{.H}\text{.S}\text{.} $ 

36.  Find the value of  $ \operatorname{Cos}(-{{1710}^{\circ }}) $ 

Ans- 

We have  $ \cos \left( -{{1710}^{\circ }} \right) $ . We also know  $ \cos \left( -x \right)=\cos x $ 

 $ \operatorname{Cos}(-{{1710}^{\circ }})=\operatorname{Cos}(1800-90) $ 

                               $ =\operatorname{Cos}\left[ 5\times 360+90 \right] $ 

                               $ =\operatorname{Cos}\dfrac{\pi }{2} $ 

                               $ =0 $ 

37.   A wheel makes  $ 360 $  revolutions in  $ 1 $  minute. Through how many radians does it turn in  $ 1 $  second.

Ans- 

Given,

 $ \text{Number of revolutions made in 60s}=360 $ 

 $ \text{Number of revolutions made in 1s}=\dfrac{360}{60} $ 

 $ \text{Angle moved in 6 revolutions}=2\pi \times 6 $ 

 $ =12\pi  $ 

38. Prove that  $ {{\operatorname{Sin}}^{2}}6x-{{\operatorname{Sin}}^{2}}4x=\operatorname{Sin}2x.\operatorname{Sin}10x $ 

Ans- 

Starting with the left-hand side and using the trigonometric addition formula for the sine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}={{\operatorname{Sin}}^{2}}6x-{{\operatorname{Sin}}^{2}}4x $ 

                $ =\sin \left( 6x+4x \right)\sin \left( 6x-4x \right) $ 

                $ =\sin 10x\sin 2x $ 

                $ =\text{R}\text{.H}\text{.S}\text{.} $ 

39. Prove that  $ \dfrac{\tan 69+\tan 66}{1\tan 69.\tan 66}=-1 $ 

Ans- 

Starting with the left-hand side and using the trigonometric difference identity for the tangent function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\dfrac{\tan {{69}^{\circ }}+\tan {{66}^{\circ }}}{1-\tan {{69}^{\circ }}\tan {{66}^{\circ }}} $ 

                 $ =\tan ({{69}^{\circ }}+{{66}^{\circ }}) $ 

                 $ =\tan \left( {{135}^{\circ }} \right) $ 

                 $ =\tan \left( {{90}^{\circ }}+{{45}^{\circ }} \right) $ 

                $ =-1 $ 

                $ =\text{R}\text{.H}\text{.S}\text{.} $ 

40.  Prove that  $\dfrac{\operatorname{Sin}x}{1+\operatorname{Cos}x}=\tan 

\dfrac{x}{2} $  

Ans- 

Starting with the left-hand side and using the trigonometric addition identities for the sine and cosine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\dfrac{\sin x}{1+\cos x} $ 

                 $ =\dfrac{2\sin \dfrac{x}{2}\cos \dfrac{x}{2}}{2{{\cos }^{2}}\dfrac{x}{2}} $ 

                 $ =\dfrac{\sin \dfrac{x}{2}}{\cos \dfrac{x}{2}} $ 

                 $ =\tan \dfrac{x}{2} $ 

                 $ =\text{R}\text{.H}\text{.S}\text{.} $ 

4 Marks Questions

Prove the following identities

1. The minute hand of a watch is  $ 1.5cm $  long. How far does its tip move in  $ 40 $  minute? 

Ans- 

Analysing the given information, we have 

 $ r=1.5cm $ 

 $ \text{Angle made in }60\min ={{360}^{\circ }} $ 

 $ \text{Angle made in 1min}={{6}^{\circ }} $ 

 $ \text{Angle made in 40min}={{6}^{\circ }}\times {{40}^{\circ }}={{240}^{\circ }} $ 

Calculating the arc distance

              $ \theta =\dfrac{l}{r} $ 

 $ 240\times \dfrac{\pi }{180}=\dfrac{l}{1.5} $ 

      $ 2\times 3.14=l $ 

              $ 6.28=l $ 

                      $ l=6.28cm $ 

2. Show that  $ tan\text{ }3x.\text{ }tan\text{ }2x.\text{ }tan\text{ }x\text{ }=\text{ }tan\text{ }3x\text{ }\text{ }tan\text{ }2x\text{ }\text{ }tan\text{ }x $  

Ans- 

Let us start with  $ \tan 3x $  and we know  $ 3x=2x+x $ 

 $ \tan 3x=\tan (2x+x) $ 

 $ \dfrac{\tan 3x}{1}=\dfrac{\tan 2x+\tan x}{1-\tan 2x.\tan x} $ 

 $ \tan 3x(1-\tan 2x.\tan x)=\tan 2x+\tan x $ 

 $ \tan 3x-\tan 3x.\tan 2x.\tan x=\tan 2x+\tan x $ 

 $ \tan 3x.\tan 2x.\tan x=\tan 3x-\tan 2x-\tan x $ 

3. Find the value of  $ \tan \dfrac{\pi }{8} $  

Ans- 

We know that

 $ \tan 2x=\dfrac{2\tan x}{1-{{\tan }^{2}}x} $ 

Therefore, we have

    $ \tan \left( 2\dfrac{\pi }{8} \right)=\dfrac{2\tan \dfrac{\pi }{8}}{1-{{\tan }^{2}}\dfrac{\pi }{8}} $ 

 $ \Rightarrow 1=\dfrac{2\tan \dfrac{\pi }{8}}{1-{{\tan }^{2}}\dfrac{\pi }{8}} $ 

Put  $ \tan \dfrac{\pi }{8}=x $ 

 $ 1=\dfrac{2x}{1-{{x}^{2}}} $ 

 $ \Rightarrow 2x=1-{{x}^{2}} $ 

 $ \Rightarrow x=\dfrac{-1\pm \sqrt{2}}{1} $ 

Since,  $ \dfrac{\pi }{8} $  lies in the first quadrant, the value must be positive, hence

$ \tan \dfrac{\pi }{8}=\sqrt{2}-1 $ 

4. Prove that  $ \dfrac{\operatorname{Sin}(x+y)}{\operatorname{Sin}(x-y)}=\dfrac{\tan x+\tan y}{\tan x-\tan y} $  

Ans- 

Starting with the left-hand side and using the trigonometric difference formula for the sine function, we get

 $ \text{L}\text{.H}\text{.S}\text{.}=\dfrac{\operatorname{Sin}(x+y)}{\operatorname{Sin}(x-y)} $ 

                $ =\dfrac{\operatorname{Sin}x.\operatorname{Cos}y+\operatorname{Cos}x.\operatorname{Sin}y}{\operatorname{Sin}x.\operatorname{Cos}y-\operatorname{Cos}x.\operatorname{Sin}y} $ 

Dividing numerator and denominator by  $ \operatorname{Cos}x.\operatorname{Cos}y $ 

           $ =\dfrac{\tan x+\tan y}{\tan x-\tan y} $ 

               $ =\text{R}\text{.H}\text{.S}\text{.} $ 

5. If in two circles, arcs of the same length subtend angles  $ {{60}^{\circ }} $  and  $ {{75}^{\circ }} $  at the center find the ratio of their radii. 

Ans- 

We know that the length of the arc and its subtended angle is related using the following formula

 $ \theta =\dfrac{1}{{{r}_{1}}} $ 

Therefore, we have

 $ 60\times \dfrac{\pi }{18}=\dfrac{1}{{{r}_{1}}} $ 

 $ {{r}_{1}}=\dfrac{3l}{\pi } $      ….. $ (1) $ 

 $ \theta =\dfrac{1}{{{r}_{2}}} $ 

 $ 75\times \dfrac{\pi }{18}=\dfrac{1}{{{r}_{2}}} $ 

 $ {{r}_{2}}=\dfrac{12l}{5\pi } $     ….. $ (2) $ 

 $ (1)\div (2) $ 

 $ \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{\dfrac{3l}{\pi }}{\dfrac{12l}{5\pi }} $ 

 $ =\dfrac{31}{\pi }\times \dfrac{5\pi }{12l} $ 

 $ =5:4 $ 

6. Prove that  $ \operatorname{Cos}6x=32{{\operatorname{Cos}}^{2}}x-48{{\operatorname{Cos}}^{4}}x+18{{\operatorname{Cos}}^{2}}x-1 $  

Ans. 

Starting with the left-hand side and using the trigonometric identities for the cosine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\operatorname{Cos}6x $ 

                 $ =\operatorname{Cos}2(3x)=2{{\operatorname{Cos}}^{2}}3x-1 $ 

                 $ =\operatorname{Cos}2(3x) $ 

                 $ =2{{(4co{{s}^{3}}x-3\cos x)}^{2}}-1 $ 

                 $ =2\left[ 16{{\operatorname{Cos}}^{6}}x+9{{\operatorname{Cos}}^{2}}x-24{{\operatorname{Cos}}^{4}}x \right]-1 $ 

                  $ =32{{\operatorname{Cos}}^{6}}x+18{{\operatorname{Cos}}^{2}}x-48{{\operatorname{Cos}}^{4}}x-1 $ 

               $ =32{{\operatorname{Cos}}^{6}}x-48{{\operatorname{Cos}}^{4}}x+18{{\operatorname{Cos}}^{2}}x1 $ 

                  $ =\text{R}\text{.H}\text{.S}\text{.} $ 

7. Solve  $ \operatorname{Sin}2x-\operatorname{Sin}4x+\operatorname{Sin}6x=0 $  

Ans- 

Starting with the left-hand side and using the trigonometric addition identity for the sine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\operatorname{Sin}6x+\operatorname{Sin}2x-\operatorname{Sin}4x $ 

                 $ =2\sin \left( \dfrac{6x+2x}{2} \right)\cos \left( \dfrac{6x-2x}{2} \right)-\sin 4x $ 

                 $ =\sin 4x\left( 2\cos 2x-1 \right) $ 

                 $ =0 $ 

Now,

 $ \sin 4x=0 $ 

      $ 4x=n\pi  $ 

        $ x=\dfrac{n\pi }{4} $ 

Also,

 $ 2\cos 2x-1=0 $ 

        $ \cos 2x=\cos \dfrac{\pi }{3} $ 

             $ 2x=2n\pi \pm \dfrac{\pi }{3} $ 

              $ x=n\pi \pm \dfrac{\pi }{6} $ 

8. In a circle of diameter  $ 40cm $ , the length of a chord is  $ 20cm $ . Find the length of the minor area of the chord. 

Ans- 

Given,

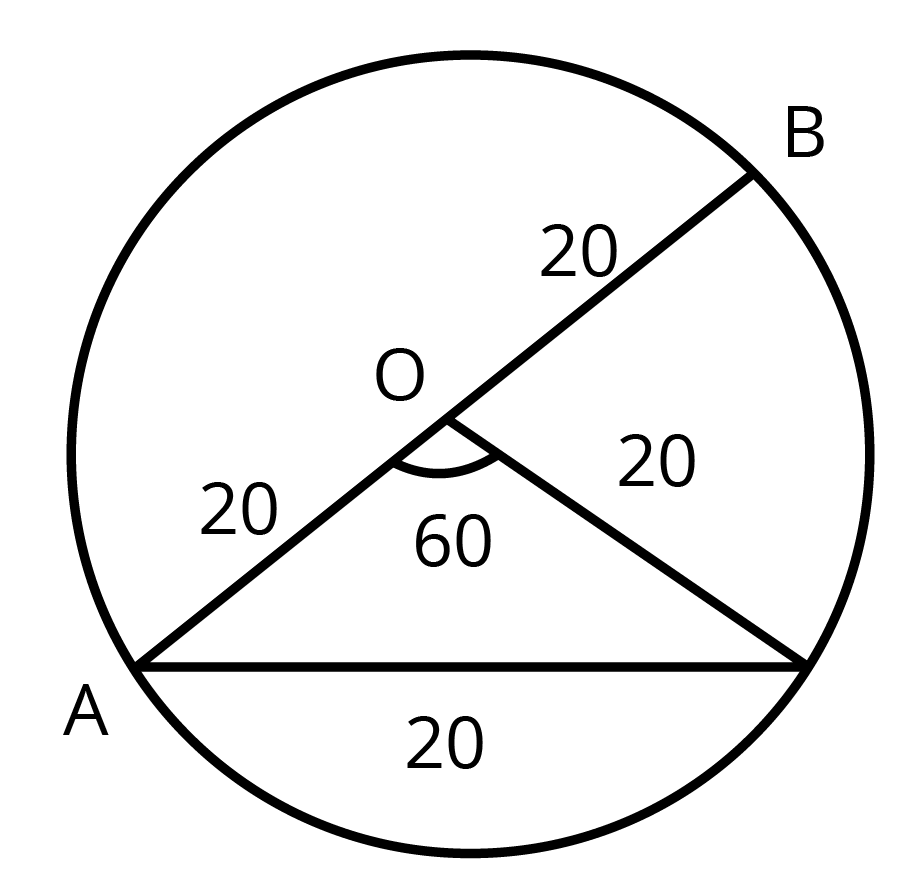
 $ \theta =\dfrac{l}{r} $ 

 $ \Rightarrow 60\times \dfrac{\pi }{180}=\dfrac{l}{20} $ 

 $ \Rightarrow l=\dfrac{20\pi }{3}\text{cm/s} $ 

9. Prove that  $ \tan 4x=\dfrac{4\tan x(1-{{\tan }^{2}}x)}{1-6{{\tan }^{2}}x+{{\tan }^{4}}x} $  

Ans- 

Starting with the left-hand side and using the trigonometric addition identities for the tangent function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\tan 4x $ 

                 $ =\dfrac{2\tan 2x}{1-{{\tan }^{2}}2x} $ 

                 $ =\dfrac{2.\dfrac{2\tan 2x}{1-{{\tan }^{2}}2x}}{1-{{\left( \dfrac{2\tan 2x}{1-{{\tan }^{2}}2x} \right)}^{2}}} $ 

                $ =\dfrac{\dfrac{4\tan x}{1-{{\tan }^{2}}x}}{\dfrac{{{(1-{{\tan }^{2}}x)}^{2}}-4{{\tan }^{2}}x}{{{(1-{{\tan }^{2}}x)}^{2}}}} $ 

                 $ =\dfrac{4\tan x}{(1-{{\tan }^{2}}x)}\times \dfrac{(1-{{\tan }^{2}}x)}{1+{{\tan }^{4}}x-2{{\tan }^{2}}x-4{{\tan }^{2}}x} $ 

                 $ =\dfrac{4\tan x(1-{{\tan }^{2}}x)}{1-6{{\tan }^{2}}x+{{\tan }^{4}}x} $ 

                 $ =\text{R}\text{.H}\text{.S}\text{.} $ 

10. Prove that  $ {{\left( Cosx+Cosy \right)}^{2}}+{{\left( SinxSiny \right)}^{2}}=4Co{{s}^{2}}\left( \dfrac{x+y}{2} \right) $  

Ans- 

Starting with the left-hand side and using the trigonometric addition identities for the cosine and sine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}={{\left( Cosx+Cosy \right)}^{2}}+{{\left( SinxSiny \right)}^{2}} $ 

                $ ={{\left( 2\operatorname{Cos}\dfrac{x+y}{2}.\operatorname{Cos}\dfrac{x-y}{2} \right)}^{2}}+{{\left( 2\operatorname{Cos}\left( \dfrac{x+y}{2} \right).\operatorname{Sin}\left( \dfrac{x-y}{2} \right) \right)}^{2}} $ 

                $ =4{{\operatorname{Cos}}^{2}}\dfrac{x+y}{2}.{{\operatorname{Cos}}^{2}}\left( \dfrac{x-y}{2} \right)+4{{\operatorname{Cos}}^{2}}\dfrac{x+y}{2}.{{\operatorname{Sin}}^{2}}\dfrac{x-y}{2} $ 

               $ =4{{\operatorname{Cos}}^{2}}\left( \dfrac{x+y}{2} \right)\left[ {{\operatorname{Cos}}^{2}}\dfrac{x-y}{2}+{{\operatorname{Sin}}^{2}}\dfrac{x-y}{2} \right] $ 

               $ =4{{\operatorname{Cos}}^{2}}\left( \dfrac{x+y}{2} \right) $ 

               $ =\text{R}\text{.H}\text{.S}\text{.} $ 

11. If  $ Cotx=-\dfrac{5}{12},x $  lies in second quadrant find the values of other five trigonometric functions 

Ans- 

Given

 $ Cotx=-\dfrac{5}{12} $ 

Using some trigonometric identities, we obtain

 $ \tan x=-\dfrac{12}{5} $ 

 $ {{\operatorname{Sec}}^{2}}x=1+{{\tan }^{2}}x $ 

 $ \operatorname{Sec}x=\pm \dfrac{13}{5} $ 

Since  $ x $  lies in the second quadrant, the cosine value will be negative

 $ \operatorname{Sec}x=-\dfrac{13}{5} $ 

 $ \operatorname{Cos}x=-\dfrac{5}{13} $ 

 $ \operatorname{Sin}x=\tan x.\operatorname{Cos}x $ 

             $ =\dfrac{-12}{5}\times \left( \dfrac{-5}{13} \right) $ 

              $ =\dfrac{12}{13} $ 

 $ \operatorname{Csc}x=\dfrac{13}{12} $ 

12. Prove that  $ \dfrac{\operatorname{Sin}5x-2\operatorname{Sin}3x+\operatorname{Sin}x}{\operatorname{Cos}5x-\operatorname{Cos}x}=\tan x $  

Ans- 

Starting with the left-hand side and using the trigonometric difference identities for the sine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\dfrac{\operatorname{Sin}5x+\operatorname{Sin}x-2\operatorname{Sin}3x}{\operatorname{Cos}5x-\operatorname{Cos}x} $ 

                 $ =\dfrac{2\operatorname{Sin}3x.\operatorname{Cos}2x-2\operatorname{Sin}3x}{-2\operatorname{Sin}3x.\operatorname{Sin}2x} $ 

                 $ =\dfrac{2\operatorname{Sin}3x(\operatorname{Cos}2x-1)}{-2\operatorname{Sin}3x.\operatorname{Sin}2x} $ 

                 $ =\dfrac{-(1-\operatorname{Cos}2x)}{-\operatorname{Sin}2x} $ 

                 $ =\dfrac{2{{\operatorname{Sin}}^{2}}x}{2\operatorname{Sin}x.\operatorname{Cos}x} $ 

                 $ =\dfrac{\operatorname{Sin}x}{\operatorname{Cos}x} $ 

                 $ =\tan x $ 

                 $ =\text{R}\text{.H}\text{.S}\text{.} $ 

13. Prove that  $ Sinx+Sin3x+Sin5x+Sin7x=4Cosx.Cos2x.Sin4x $  

Ans- 

Starting with the left-hand side and using the trigonometric addition identities for the sine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=Sinx+Sin3x+Sin5x+Sin7x $ 

                 $ =\operatorname{Sin}x+\operatorname{Sin}7x+\operatorname{Sin}3x+\operatorname{Sin}5x $ 

                 $ =2\operatorname{Sin}\left( \dfrac{x+7x}{2} \right).\operatorname{Cos}\left( \dfrac{x-7x}{2} \right)+2\operatorname{Sin}\left( \dfrac{3x+5x}{2} \right)\operatorname{Cos}\left( \dfrac{3x-5x}{2} \right) $ 

                 $ =2\operatorname{Sin}4x.\operatorname{Cos}3x+2\operatorname{Sin}4x.\operatorname{Cos}x $ 

                 $ =2\operatorname{Sin}4x[\operatorname{Cos}3x+\operatorname{Cos}x] $ 

                 $ =2\operatorname{Sin}4x\left[ 2\operatorname{Cos}\left( \dfrac{3x+x}{2} \right).\operatorname{Cos}\left( \dfrac{3x-x}{2} \right) \right] $ 

                 $ =2\operatorname{Sin}4x[2\operatorname{Cos}2x.\operatorname{Cos}x] $ 

                 $ =4\operatorname{Cos}x.\operatorname{Cos}2x.\operatorname{Sin}4x $ 

                 $ =\text{R}\text{.H}\text{.S}\text{.} $ 

14. Find the angle between the minute hand and hour hand of a clock when the time is  $ 7.20 $  

Ans- 

We know that the angle made by minute hand in  $ 15\min =15\times 6={{90}^{\circ }} $ 

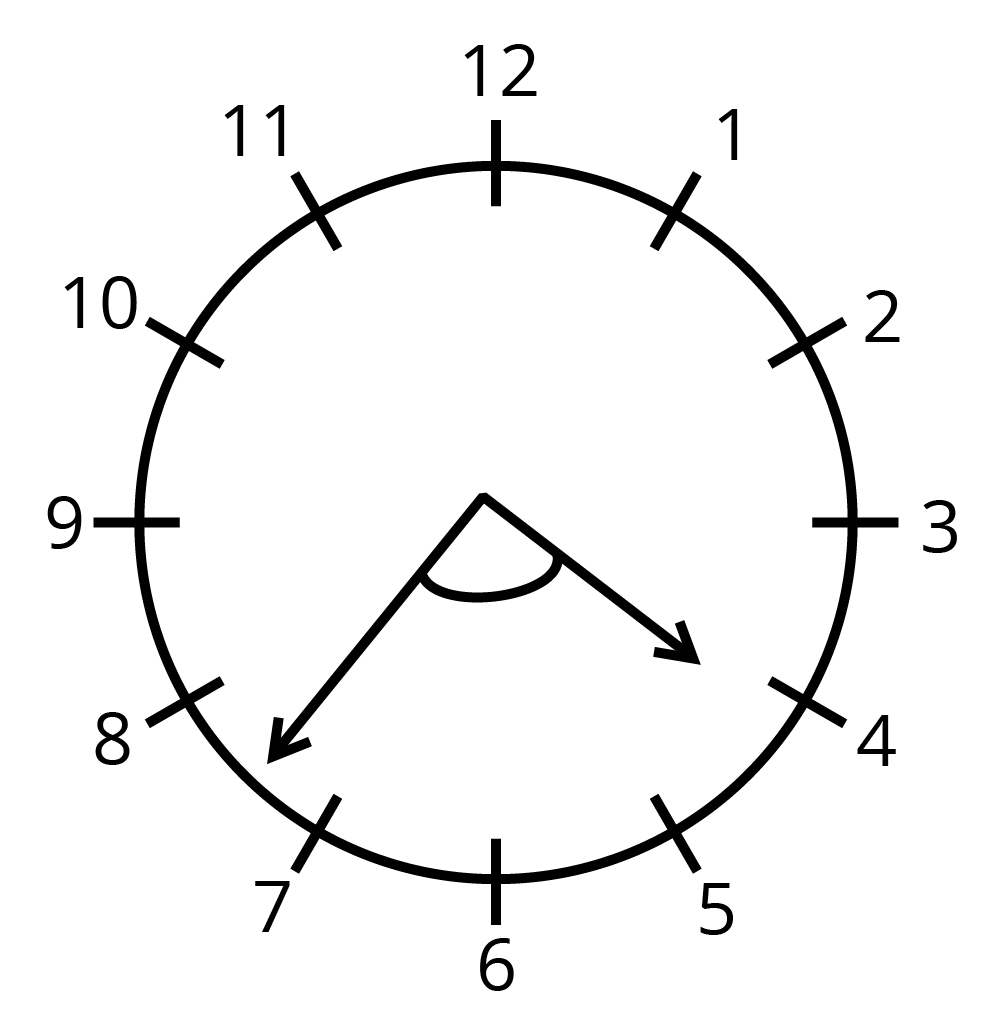
We also know that the angle made by the hour hand in  $ 1hr={{30}^{\circ }} $ 

In  $ 60 $  minute  $ =\dfrac{30}{60} $ 

 $ =\dfrac{1}{2} $ 

 $ [\because  $ Angle Travelled by  $ hr $ hand in  $ 12hr={{360}^{\circ }}] $ 

In  $ 20 $ minutes  $ =\dfrac{1}{2}\times 20 $ 

                         $ ={{10}^{\circ }} $ 

Angle made  $ =90+10 $ 

                       $ ={{100}^{\circ }} $ 

15. Show that  $ \sqrt{2+\sqrt{2+2\operatorname{Cos}4\theta }}=2\operatorname{Cos}\theta  $  

Ans- 

Starting with the left-hand side and using the trigonometric addition identity for the cosine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\sqrt{2+\sqrt{2+2\operatorname{Cos}4\theta }} $ 

                 $ =\sqrt{2+\sqrt{2(1+\operatorname{Cos}4\theta )}} $ 

                 $ =\sqrt{2+\sqrt{2.2{{\operatorname{Cos}}^{2}}2\theta }} $ 

                 $ =\sqrt{2+2\operatorname{Cos}2\theta } $ 

                 $ =\sqrt{2(1+\operatorname{Cos}2\theta )} $ 

                 $ =\sqrt{2.2{{\operatorname{Cos}}^{2}}\theta } $ 

                 $ =2\operatorname{Cos}\theta  $ 

                 $ =\text{R}\text{.H}\text{.S}\text{.} $ 

16. Prove that  $ Cot4x\left( Sin5x+Sin3x \right)=Cotx\left( Sin5xSin3x \right) $  

Ans- 

Starting with the left-hand side and using the trigonometric addition identity for the sine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=Cot4x\left( Sin5x+Sin3x \right) $ 

                $ =\dfrac{\operatorname{Cos}4x}{\operatorname{Sin}4x}\left[ 2\operatorname{Sin}\dfrac{5x+3x}{2}.\operatorname{Cos}\dfrac{5x-3x}{2} \right] $ 

                $ =\dfrac{\operatorname{Cos}4x}{\operatorname{Sin}4x}2\operatorname{Sin}4x.\operatorname{Cos}x $ 

                $ =2\operatorname{Cos}4x.\operatorname{Cos}x $ 

Then, we move on to the right-hand side and using the trigonometric addition identity for the sine function, we obtain

   $ \text{R}\text{.H}\text{.S}\text{.}=Cotx\left( Sin5xSin3x \right) $ 

                   $ =\dfrac{\operatorname{Cos}x}{\operatorname{Sin}x}\left[ 2\operatorname{Cos}\dfrac{5x+3x}{2}.\operatorname{Sin}\dfrac{5x-3x}{2} \right] $ 

                   $ =\dfrac{\operatorname{Cos}x}{\operatorname{Sin}x}[2\operatorname{Cos}4x.\operatorname{Sin}x] $ 

                   $ =2\operatorname{Cos}4x.\operatorname{Cos}x $ 

Therefore, 

   $ \text{L}\text{.H}\text{.S}=\text{R}\text{.H}\text{.S} $ 

6 Marks Questions

1. Find the general solution of  $ sin2x+sin4x+sin6x=0 $ 

Ans- 

We have that  $ \sin 2x+\sin 4x+\sin 6x=0 $ 

 $ \Rightarrow \left( \sin 2x+\sin 6x \right)+\sin 4x=0 $ 

 $ \Rightarrow \left( 2\sin \left( \dfrac{2x+6x}{2} \right)\cos \left( \dfrac{2x-6x}{2} \right) \right)+\sin 4x=0 $ 

 $ \Rightarrow 2\sin 4x\cos 2x+\sin 4x=0 $ 

 $ \Rightarrow \sin 4x\left( 2\cos 2x+1 \right)=0 $ 

Now

 $ \sin 4x=0 $ 

 $ \Rightarrow x=n\pi  $ 

 $ 2\cos 2x+1=0 $ 

 $ \Rightarrow x=n\pi \pm \dfrac{\pi }{3} $ 

2. Find the general solution of  $ \cos \theta \cos 2\theta \cos 3\theta =\dfrac{1}{4} $  

Ans- 

We have that  $ \cos \theta \cos 2\theta \cos 3\theta =\dfrac{1}{4} $ 

 $ \Rightarrow 4\cos \theta \cos 2\theta \cos 3\theta =1 $ 

Using the trigonometric addition identity for the cosine function, we obtain

 $ \Rightarrow 2\left( 2\cos \theta \cos 3\theta  \right)\cos 2\theta -1=0 $ 

 $ \Rightarrow 2\left( \cos 4\theta +\cos 2\theta  \right)\cos 2\theta -1=0 $ 

 $ \Rightarrow 2\left( 2{{\cos }^{2}}2\theta -1+\cos 2\theta  \right)\cos 2\theta -1=0 $ 

 $ \Rightarrow \left( 2{{\cos }^{2}}2\theta -1 \right)\left( 2\cos 2\theta +1 \right)=0 $ 

Now,

 $ 2{{\cos }^{2}}2\theta -1=0 $ 

 $ \Rightarrow \cos 4\theta =0 $ 

 $ \Rightarrow 4\theta =\left( 2n+1 \right)\dfrac{\pi }{2} $ 

 $ \Rightarrow \theta =\left( 2n+1 \right)\dfrac{\pi }{8} $ 

Also,

 $ 2\cos 2\theta +1=0 $ 

 $ \Rightarrow \cos 2\theta =-\dfrac{1}{2} $ 

 $ \Rightarrow \theta =n\pi \pm \dfrac{\pi }{3} $ 

3. If  $ \operatorname{Sin}\alpha +\operatorname{Sin}\beta =a $  and  $ \operatorname{Cos}\alpha +\operatorname{Cos}\beta =b $  

Show that  $ \operatorname{Cos}(\alpha +\beta )=\dfrac{{{b}^{2}}-{{a}^{2}}}{{{b}^{2}}+{{a}^{2}}} $  

Ans- 

Squaring both the equations and adding them together,

 $ {{b}^{2}}+{{a}^{2}}={{(\operatorname{Cos}\alpha +\operatorname{Cos}\beta )}^{2}}+{{(\operatorname{Sin}\alpha +\operatorname{Sin}\beta )}^{2}} $ 

                 $ ={{\operatorname{Cos}}^{2}}\alpha +{{\operatorname{Cos}}^{2}}\beta +2\operatorname{Cos}\alpha .\operatorname{Cos}\beta +{{\operatorname{Sin}}^{2}}\alpha +{{\operatorname{Sin}}^{2}}\beta +2\operatorname{Sin}\alpha .\operatorname{Sin}\beta  $ 

                 $ =1+1+2(\operatorname{Cos}\alpha .\operatorname{Cos}\beta +\operatorname{Sin}\alpha .\operatorname{Sin}\beta ) $ 

            $ =2+2\operatorname{Cos}(\alpha -\beta ) $        $ (1) $ 

 $ {{b}^{2}}-{{a}^{2}}={{(\operatorname{Cos}\alpha +\operatorname{Cos}\beta )}^{2}}-{{(\operatorname{Sin}\alpha +\operatorname{Sin}\beta )}^{2}} $ 

                 $ =({{\operatorname{Cos}}^{2}}\alpha -{{\operatorname{Sin}}^{2}}\beta )+({{\operatorname{Cos}}^{2}}\beta -{{\operatorname{Sin}}^{2}}\alpha )+2\operatorname{Cos}(\alpha +\beta ) $ 

                 $ =\operatorname{Cos}(\alpha +\beta )\operatorname{Cos}(\alpha -\beta )+\operatorname{Cos}(\beta +\alpha )\operatorname{Cos}(\alpha -\beta )+2\operatorname{Cos}(\alpha +\beta ) $ 

                 $ =2\operatorname{Cos}(\alpha +\beta ).\operatorname{Cos}(\alpha -\beta )+2\operatorname{Cos}(\alpha +\beta ) $ 

                 $ =\operatorname{Cos}(\alpha +\beta )[2\operatorname{Cos}(\alpha -\beta )+2] $ 

              $ =\operatorname{Cos}(\alpha +\beta ).({{b}^{2}}+{{a}^{2}}) $       from  $ (1) $ 

Dividing equation  $ \left( 1 \right) $  with  $ {{b}^{2}}+{{a}^{2}} $ , we get

 $ \dfrac{{{b}^{2}}-{{a}^{2}}}{{{b}^{2}}+{{a}^{2}}}=\operatorname{Cos}(\alpha +\beta ) $ 

4. Prove  $ Cos\alpha +Cos\beta +Cos\gamma +Cos\left( \alpha +\beta +\gamma  \right)=4\operatorname{Cos}\left( \dfrac{\alpha +\beta }{2} \right).\operatorname{Cos}\left( \dfrac{\beta +\gamma }{2} \right).\operatorname{Cos}\left( \dfrac{\gamma +\alpha }{2} \right) $ 

Ans- 

Starting with the left-hand side and using the trigonometric addition identities for the cosine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=Cos\alpha +Cos\beta +Cos\gamma +Cos\left( \alpha +\beta +\gamma  \right) $ 

                 $ =2\operatorname{Cos}\left( \dfrac{\alpha +\beta }{2} \right).\operatorname{Cos}\left( \dfrac{\alpha -\beta }{2} \right)+2\operatorname{Cos}\left( \dfrac{\alpha +\beta +\gamma +\gamma }{2} \right).\operatorname{Cos}\left( \dfrac{\alpha +\beta +\gamma -\gamma }{2} \right) $ 

                $ =2\operatorname{Cos}\left( \dfrac{\alpha +\beta }{2} \right).\operatorname{Cos}\left( \dfrac{\alpha -\beta }{2} \right)+2\operatorname{Cos}\left( \dfrac{\alpha +\beta }{2} \right).\operatorname{Cos}\left( \dfrac{\alpha +\beta +2\gamma }{2} \right) $ 

                $ =2\operatorname{Cos}\left( \dfrac{\alpha +\beta }{2} \right)\left[ \operatorname{Cos}\left( \dfrac{\alpha -\beta }{2} \right)+\operatorname{Cos}\left( \dfrac{\alpha +\beta +2\gamma }{2} \right) \right] $ 

            $ =2\operatorname{Cos}\left( \dfrac{\alpha +\beta }{2} \right)\left[ 2\operatorname{Cos}\left( \dfrac{\dfrac{\alpha -\beta }{2}+\dfrac{\alpha +\beta +2\gamma }{2}}{2} \right).\operatorname{Cos}\left( \dfrac{\dfrac{\alpha +\beta +2\gamma }{2}-\dfrac{\alpha -\beta }{2}}{2} \right) \right] $ 

                $ =2\operatorname{Cos}\left( \dfrac{\alpha +\beta }{2} \right)\left[ 2\operatorname{Cos}\left( \dfrac{\alpha +\gamma }{2} \right).\operatorname{Cos}\left( \dfrac{\beta +\gamma }{2} \right) \right] $ 

               $ =4\operatorname{Cos}\left( \dfrac{\alpha +\beta }{2} \right).\operatorname{Cos}\left( \dfrac{\beta +\gamma }{2} \right).\operatorname{Cos}\left( \dfrac{\gamma +\alpha }{2} \right) $ 

               $ =\text{R}\text{.H}\text{.S}\text{.} $ 

5. Prove that  $ \operatorname{Sin}3x+\operatorname{Sin}2x-\operatorname{Sin}2x=4\operatorname{Sin}x.\operatorname{Cos}\dfrac{x}{2}.\operatorname{Cos}\dfrac{3x}{2} $  

Ans- 

Starting with the left-hand side and using the trigonometric addition identity for the sine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\sin 3x+\sin x-\sin 2x $ 

                 $ =2\cos \left( \dfrac{3x+x}{2} \right).\operatorname{Sin}\left( \dfrac{3x+x}{2} \right)+\operatorname{Sin}2x $ 

                 $ =2\cos 2x.\sin x+\sin 2x $ 

                 $ =2\cos 2x.\sin x+2\sin x\cos x $ 

                 $ =2\sin x[\cos 2x+\cos x] $ 

                 $ =2\sin x\left[ 2\cos x\dfrac{3x}{2}.\cos \dfrac{x}{2} \right] $ 

                 $ =4\sin x\cos x\dfrac{3x}{2}\cos \dfrac{x}{2} $ 

                 $ =\text{R}\text{.H}\text{.S}\text{.} $ 

6. Prove that  $ 2\cos \dfrac{\pi }{13}.\cos \dfrac{9\pi }{13}+\cos \dfrac{3\pi }{13}+\cos \dfrac{5\pi }{13}=0 $  

Ans- 

Starting with the left-hand side using the trigonometric addition identities for the cosine and sine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=2\cos \dfrac{\pi }{13}.\cos \dfrac{9\pi }{13}+\cos \dfrac{3\pi }{13}+\cos \dfrac{5\pi }{13} $ 

                 $ =\cos \left( \dfrac{\pi }{13}+\dfrac{9\pi }{13} \right)+\cos \left( \dfrac{\pi }{13}-\dfrac{9\pi }{13} \right)+\cos \dfrac{3\pi }{13}+\cos \dfrac{5\pi }{13} $ 

                 $ =\cos \dfrac{10\pi }{13}+\cos \dfrac{18\pi }{13}+\cos \dfrac{3\pi }{13}+\cos \dfrac{5\pi }{13} $ 

                 $ =\cos \left( \pi -\dfrac{3\pi }{13} \right)+\cos \left( \pi -\dfrac{5\pi }{13} \right)+\cos \dfrac{3\pi }{13}+\cos \dfrac{5\pi }{13} $ 

                 $ =-\cos \dfrac{3\pi }{13}-\cos \dfrac{5\pi }{13}+\dfrac{3\pi }{13}+\cos \dfrac{5\pi }{13} $ 

                 $ =0 $ 

                 $ =\text{R}\text{.H}\text{.S}\text{.} $ 

7.  Find the value of  $ \tan (\alpha +\beta ) $ given that  $ \cot \alpha =\dfrac{1}{2},\alpha \in \left( \pi ,\dfrac{3\pi }{2} \right) $  and  $ \operatorname{Sec}\beta =-\dfrac{5}{3},\beta \in \left( \dfrac{\pi }{2},\pi  \right) $  

Ans- 

We know that,

 $ \tan \left( \alpha +\beta  \right)=\dfrac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta } $ 

Given,

 $ Cot\alpha =\dfrac{1}{2} $ 

 $ \tan \alpha =2 $ 

Now, let us find  $ \tan \beta  $ 

 $ 1+{{\tan }^{2}}\beta ={{\operatorname{Sec}}^{2}}\beta  $ 

 $ 1+{{\tan }^{2}}\beta ={{\left( \dfrac{-5}{3} \right)}^{2}}\left[ \because \operatorname{Sec}\beta =\dfrac{-5}{3} \right] $ 

 $ \tan \beta =\pm \dfrac{4}{3} $ 

 $ \tan \beta =-\dfrac{4}{3}\left[ \because \beta \in \left( \dfrac{\dfrac{\pi }{2}}{x} \right) \right] $ 

Therefore, we have that

 $ \tan \left( \alpha +\beta  \right)=\dfrac{2-\dfrac{4}{3}}{1-2\left( \dfrac{-4}{3} \right)} $ 

                     $ =\dfrac{2}{11} $ 

8. Prove that  $ \dfrac{\operatorname{Sec}8A-1}{\operatorname{Sec}4A-1}=\dfrac{\tan 8A}{\tan 2A} $  

Ans- 

Starting with the left-hand side and using the trigonometric elementary identities of the cosine function and sine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\dfrac{\sec 8A-1}{\sec 4A-1} $ 

                $ =\dfrac{\dfrac{1}{\operatorname{Cos}8A}-1}{\dfrac{1}{\operatorname{Cos}4A}-1} $ 

                $ =\dfrac{1-\operatorname{Cos}8A}{1-\operatorname{Cos}4A}\times \dfrac{\operatorname{Cos}4A}{\operatorname{Cos}8A} $ 

                $ =\dfrac{2{{\operatorname{Sin}}^{2}}4A}{2{{\operatorname{Sin}}^{2}}2A}.\dfrac{\operatorname{Cos}4A}{\operatorname{Cos}8A} $ 

                $ =\dfrac{(2\operatorname{Sin}4A.\operatorname{Cos}4A).\operatorname{Sin}4A}{2{{\operatorname{Sin}}^{2}}2A.\operatorname{Cos}8A} $ 

                $ =\dfrac{\operatorname{Sin}8A(2\operatorname{Sin}2A.\operatorname{Cos}2A)}{2{{\operatorname{Sin}}^{2}}2A.\operatorname{Cos}8A} $ 

                $ =\dfrac{\operatorname{Sin}8A\operatorname{Cos}2A}{\operatorname{Sin}2A.\operatorname{Cos}2A} $ 

                $ =\dfrac{\tan 8A}{\tan 2A} $ 

                $ =\text{R}\text{.H}\text{.S}\text{.} $ 

9. Prove that  $ {{\operatorname{Cos}}^{2}}x+{{\operatorname{Cos}}^{2}}\left( x+\dfrac{\pi }{3} \right)+{{\operatorname{Cos}}^{2}}\left( x-\dfrac{\pi }{3} \right)=\dfrac{3}{2} $  

Ans- 

Starting with the left-hand side and using trigonometric addition identities of the cosine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\dfrac{1+\operatorname{Cos}2x}{2}+\dfrac{1+\operatorname{Cos}\left( 2x+\dfrac{2\pi }{3} \right)}{2}+\dfrac{1+\operatorname{Cos}\left( 2x-\dfrac{2\pi }{3} \right)}{2} $ 

                $ =\dfrac{1}{2}\left[ 1+1+1+\operatorname{Cos}2x+\operatorname{Cos}\left( 2x+\dfrac{2\pi }{3} \right)+\operatorname{Cos}\left( 2x-\dfrac{2\pi }{3} \right) \right] $ 

                $ =\dfrac{1}{2}\left[ 3+\operatorname{Cos}2x+\operatorname{Cos}\left( 2x+\dfrac{2\pi }{3} \right)+\operatorname{Cos}\left( 2x-\dfrac{2\pi }{3} \right) \right] $ 

                $ =\dfrac{1}{2}\left[ 3+\operatorname{Cos}2x+2\operatorname{Cos}\left( \dfrac{2x+\dfrac{2\pi }{3}+2x-\dfrac{2\pi }{3}}{2} \right).\operatorname{Cos}\left( \dfrac{2x+\dfrac{2\pi }{3}-2x+\dfrac{2\pi }{3}}{2} \right) \right] $ 

                $ =\dfrac{1}{2}\left[ 3+\operatorname{Cos}2x+2\operatorname{Cos}2x.\operatorname{Cos}\dfrac{4\pi }{6} \right] $ 

                $ =\dfrac{1}{2}\left[ 3+\operatorname{Cos}2x+2\operatorname{Cos}2x.\operatorname{Cos}\dfrac{2\pi }{3} \right] $ 

            $ =\dfrac{1}{2}\left[ 3+\operatorname{Cos}2x+2\operatorname{Cos}2x.\operatorname{Cos}\left( \pi -\dfrac{\pi }{3} \right) \right] $ 

                $ =\dfrac{1}{2}\left[ 3+\operatorname{Cos}2x+2\operatorname{Cos}2x.\left( \dfrac{-1}{2} \right) \right] $ 

                $ =\dfrac{3}{2} $ 

                $ =\text{R}\text{.H}\text{.S}\text{.} $ 

10.  Prove that  $ \operatorname{Cos}2x.\operatorname{Cos}\dfrac{x}{2}-\operatorname{Cos}3x.\operatorname{Cos}\dfrac{9x}{2}=\operatorname{Sin}5x\operatorname{Sin}\dfrac{5x}{2} $  

Ans- 

Starting with the left-hand side and using trigonometric addition identities for the cosine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\dfrac{1}{2}\left[ 2\operatorname{Cos}2x.\operatorname{Cos}\dfrac{x}{2}-2\operatorname{Cos}3x.\operatorname{Cos}\dfrac{9x}{2} \right] $ 

                $ =\dfrac{1}{2}\left[ \operatorname{Cos}\left( 2x+\dfrac{x}{2} \right)+\operatorname{Cos}\left( 2x-\dfrac{x}{2} \right)-\operatorname{Cos}\left( \dfrac{9x}{2}+3x \right)-\operatorname{Cos}\left( \dfrac{9x}{2}-3x \right) \right] $ 

                $ =\dfrac{1}{2}\left[ \operatorname{Cos}\dfrac{5x}{2}+\operatorname{Cos}\dfrac{3x}{2}-\operatorname{Cos}\dfrac{15x}{2}-\operatorname{Cos}\dfrac{3x}{2} \right] $ 

               $ =\dfrac{1}{2}\left[ \operatorname{Cos}\dfrac{5x}{2}-\operatorname{Cos}\dfrac{15x}{2} \right] $ 

              $ =\dfrac{1}{2}\left[ -2\operatorname{Sin}\left( \dfrac{\dfrac{5x}{2}+\dfrac{15x}{2}}{2} \right).\operatorname{Sin}\left( \dfrac{\dfrac{5x}{2}-\dfrac{15x}{2}}{2} \right) \right] $ 

              $ =-\operatorname{Sin}5x.\operatorname{Sin}\left( \dfrac{-5x}{2} \right) $ 

              $ =\operatorname{Sin}5x.\operatorname{Sin}\dfrac{5x}{2} $ 

              $ =\text{R}\text{.H}\text{.S}\text{.} $ 

11.  Prove that  $ \operatorname{Cos}20{}^\circ .\operatorname{Cos}40{}^\circ .\operatorname{Cos}60{}^\circ .\operatorname{Cos}80{}^\circ =\dfrac{1}{16} $  

Ans- 

Starting with the left-hand side and using the trigonometric addition identities of the cosine function, we obtain

 $ \text{L}\text{.H}\text{.S}\text{.}=\operatorname{Cos}{{20}^{{}^\circ }}.\operatorname{Cos}{{40}^{{}^\circ }}.\operatorname{Cos}{{60}^{{}^\circ }}.\operatorname{Cos}{{80}^{{}^\circ }} $ 

                 $ =\operatorname{Cos}{{60}^{{}^\circ }}.\operatorname{Cos}{{20}^{{}^\circ }}.\operatorname{Cos}{{40}^{{}^\circ }}.\operatorname{Cos}{{80}^{{}^\circ }} $ 

                 $ =\dfrac{1}{2}.\dfrac{1}{2}\operatorname{Cos}{{40}^{{}^\circ }}\left( 2\operatorname{Cos}{{20}^{{}^\circ }}.\operatorname{Cos}{{80}^{{}^\circ }} \right) $ 

                 $ =\dfrac{1}{4}\operatorname{Cos}{{40}^{{}^\circ }}\left[ \operatorname{Cos}(80+20)+\operatorname{Cos}(80-20) \right] $ 

                 $ =\dfrac{1}{4}\operatorname{Cos}{{40}^{{}^\circ }}\left[ \operatorname{Cos}{{100}^{{}^\circ }}+\operatorname{Cos}{{60}^{{}^\circ }} \right] $ 

                $ =\dfrac{1}{4}\operatorname{Cos}{{40}^{{}^\circ }}\left[ \operatorname{Cos}{{100}^{{}^\circ }}+\dfrac{1}{2} \right] $ 

                $ =\dfrac{1}{8}(2\operatorname{Cos}{{100}^{{}^\circ }}\operatorname{Cos}{{40}^{{}^\circ }})+\dfrac{1}{8}\operatorname{Cos}{{40}^{{}^\circ }} $ 

           $ =\dfrac{1}{8}\left[ \operatorname{Cos}{{(100+40)}^{{}^\circ }}+\operatorname{Cos}{{(100-40)}^{{}^\circ }} \right]+\dfrac{1}{8}\operatorname{Cos}{{40}^{{}^\circ }} $ 

               $ =\dfrac{1}{8}\left[ \operatorname{Cos}{{140}^{{}^\circ }}+\operatorname{Cos}{{60}^{{}^\circ }} \right]+\dfrac{1}{8}\operatorname{Cos}{{40}^{{}^\circ }} $ 

               $ =\dfrac{1}{8}\left[ \operatorname{Cos}{{140}^{{}^\circ }}+\dfrac{1}{2} \right]+\dfrac{1}{8}\operatorname{Cos}{{40}^{{}^\circ }} $ 

              $ =\dfrac{1}{8}\operatorname{Cos}{{(180-40)}^{{}^\circ }}+\dfrac{1}{16}+\dfrac{1}{8}\operatorname{Cos}{{40}^{{}^\circ }} $ 

              $ =-\dfrac{1}{8}\operatorname{Cos}{{40}^{{}^\circ }}+\dfrac{1}{16}+\dfrac{1}{8}\operatorname{Cos}{{40}^{{}^\circ }} $ 

              $ =\dfrac{1}{16} $ 

             $ =\text{R}\text{.H}\text{.S}\text{.} $ 

12.  If  $ \tan x=\dfrac{3}{4},\pi <x<\dfrac{3\pi }{2}, $ Find the value of  $ \operatorname{Sin}\dfrac{x}{2},\operatorname{Cos}\dfrac{x}{2} $  and  $ \tan \dfrac{x}{2} $  

Ans- 

Given that

 $ \pi <x<\dfrac{3\pi }{2} $  implying that  $ x $  is in the third quadrant 

 $ \Rightarrow \dfrac{\pi }{2}<\dfrac{x}{2}<\dfrac{3\pi }{2} $ 

Therefore, we have that  $ \operatorname{Sin}\dfrac{x}{2} $  is positive and  $ \operatorname{Cos}\dfrac{x}{2} $  is negative.

Let us find for  $ \tan \dfrac{x}{2} $ 

We know

 $ 1+{{\tan }^{2}}x={{\operatorname{Sec}}^{2}}x\dfrac{5}{4} $ 

 $ 1+{{\left( \dfrac{3}{4} \right)}^{2}}={{\operatorname{Sec}}^{2}}x $ 

    $ {{\operatorname{Sec}}^{2}}x=\pm \dfrac{25}{16} $ 

      $ \operatorname{Cos}x=\pm \dfrac{4}{5} $ 

      $ \operatorname{Cos}x=-\dfrac{4}{5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ \because \pi <x<\dfrac{3\pi }{2} \right] $ 

Let us find the required values 

 $ \operatorname{Sin}\dfrac{x}{2}=\sqrt{\dfrac{1-\operatorname{Cos}x}{2}} $ 

              $ =\sqrt{\dfrac{1+\dfrac{4}{5}}{2}} $ 

              $ =\sqrt{\dfrac{9}{10}} $ 

              $ =\dfrac{3}{\sqrt{10}} $ 

  $ \operatorname{Cos}\dfrac{x}{2}=-\sqrt{\dfrac{1-\operatorname{Cos}x}{2}} $ 

                  $ =-\sqrt{\dfrac{1-\dfrac{4}{5}}{2}} $ 

                  $ =-\sqrt{\dfrac{1}{10}} $ 

                 $ =\dfrac{-1}{\sqrt{10}} $ 

  $ \tan \dfrac{x}{2}=\dfrac{\dfrac{3}{\sqrt{10}}}{\dfrac{-1}{\sqrt{10}}} $ 

                $ =-3 $ 

The Formula for Function of Trigonometric Ratios

Trigonometric Table

Important Questions for Class 11 Maths Chapter 3 Based on Exercise

Q. An engine produces 360 revolutions in one minute. Through how many radians will it turn in one second?

Solution:

Provided,

The total number of revolutions made by an engine in one minute = 360

1 minute = 60 seconds

Therefore, number of revolutions in 1 second = 360/60 = 6

Angle formed in 1 revolution = 360°

Angles formed in 6 revolutions = 6 × 360°

Radian measure of the angle in a total of six revolutions = 6 × 360 × π/180

= 6 × 2 × π

= 12π

So, the engine turns 12π radians in one second.

Practice Questions

• Prove that:
  (sin 5x + sin 3x)/(cos 5x + cos 3x) = tan 4x

• Find the value of tan 765° cot 675° + tan 225° cot 405°

• Solve the equation: tan² θ + cot² θ = 2

• Write the value of 2sin 75° sin 15°

• Show that:
  tan 4A = (cos8Acos5A - cos12Acos9A) / (sin8Acos5A + cos12Asin9A)

• Find the general solution of the following equation:
  tan2θ +(1 – √3) tan θ – √3 = 0

• Prove that:
  3sinπ/6secπ/3 - 4sin5π/6cotπ/4 = 1

• Find the value:
  cos4π/8 + cos43π/8 + cos45π/8 + cos47π/8

• Show that:
  tan 15° + cot 15° = 4

• Find the most general value of θ satisfying the equation tan θ = -1 and cos θ = 1/√2

Advantages of Opting Vedantu for Important Questions of Class 11 Maths: Chapter 3 Trigonometric

Vedantu offers several benefits to students using their platform for the "Important Questions for CBSE Class 11 Maths Chapter 3 - Trigonometric Functions (2025-26)":

• Comprehensive Coverage: Vedantu's important questions are curated to cover a wide spectrum of topics within the chapter, ensuring a comprehensive understanding of trigonometric functions.

• Strategic Exam Preparation: These questions are strategically selected to align with the CBSE curriculum and examination patterns, preparing students effectively for their exams.

• Conceptual Clarity: Vedantu's platform emphasizes conceptual clarity by providing in-depth explanations and solutions for each question, helping students grasp the underlying principles.

• Variety of Problem Types: The diverse range of questions offered by Vedantu challenges students to apply trigonometric concepts in various problem-solving scenarios, enhancing their problem-solving skills.

• Self-Assessment and Practice: Students can use these questions for self-assessment and regular practice, enabling them to gauge their progress and identify areas that need improvement.

• Flexibility and Convenience: Vedantu's platform allows students to access these questions anytime, anywhere, providing flexibility in their study routine.

Conclusion

Trigonometric Functions is an important chapter in Class 11 Maths that helps build a strong foundation for advanced topics in calculus and geometry. Practising important questions from this chapter allows students to understand concepts like trigonometric identities, inverse functions, and their applications more clearly. The free PDF provides a variety of problems, making it easier for students to prepare effectively, boost their confidence, and perform well in exams. Regular practice of these questions ensures a better understanding of the topic and helps in scoring good marks.

Important Study Materials for Class 11 Maths Chapter 3 Trigonometric Functions

CBSE Class 11 Maths Chapter-wise Important Questions

CBSE Class 11 Maths Chapter-wise Important Questions and Answers cover topics from all 14 chapters, helping students prepare thoroughly by focusing on key topics for easier revision.

Important Related Links for CBSE Class 11 Maths