




An Overview of Class 11 Physics Motion Under Gravity And Acceleration Due To Gravity Experiment
Scientists like Isaac Newton and Galileo Galilei investigated the link between the length and duration of one swing (the period) for a very long time. This research enabled them to derive an exact value for the gravitational acceleration, or 'g, with great accuracy.
The motion under gravity and acceleration due to gravity is the acceleration brought on by the earth's gravitational pull. A person who jumps out of an aeroplane with a parachute falls freely for some time. The gravity of the earth causes him to accelerate. However, Acceleration due to gravity depends upon the planet's radius, mass, and gravitational constant.
In this experiment, we will replicate their experiment and choose a suitable value for "g." Lastly, it will be measured and compared to the reference value of 9.806 m/s2. The experiment uses the basic pendulum experiment to determine an approximation of 'g' (gravity). We investigate several other factors, such as displacement, angle, damping, and bob mass.
Table of Content
Aim
Observations
Results
Conclusion
Aim
This study aims to calculate the gravitational constant, 9.81 m/s2, and to explain the results' uncertainty.
Theory
A straightforward pendulum is a weight, the bob, suspended from and fastened to a non-elastic length (L) string with a light mass that permits a straightforward back-and-forth swinging motion. When the bob swings back and forth in an irregular pattern, it is said to be oscillating; this motion is also known as simple harmonic motion. The equilibrium transition from point A to point B is an oscillation. The specific swinging motions of the pendulum are propelled by the conversion of kinetic to potential energy. The period T is the length of time required to accomplish one oscillation. The maximum distance the mass can be moved away from its equilibrium position is known as the oscillation's amplitude.
\[{\rm{T = 2\pi }}\sqrt {\dfrac{{\rm{L}}}{{\rm{g}}}} \]
This is possible due to the equation's relationship between the period of a simple pendulum and the acceleration brought on by gravity.
where T = period, L is the pendulum's length, and g is its gravitational acceleration.
Apparatus Required
Protractor
String
Stopwatch
Tape
Ruler
Mass (10 gm)
Procedure
A pendulum bob should be attached to the string.
Measure the pendulum arm's length using the meter ruler.
Determine the length of the pendulum arm's square root.
By pulling the pendulum bob back with your hand, you can cause it to move slightly out of equilibrium.
When the pendulum bob is released, it will swing freely; at this point, simultaneously click "START" on the stopwatch.
Click "STOP" on the stopwatch after 10 full oscillations, note the supplied time t, and get the periodic time T by dividing the total time by 10.
Repeat the first three steps a final two times, recording the values as T1, T2, and T3, respectively.
Record the average period's value next to its corresponding pendulum bob mass.
Repeat the same data collection procedures four times, varying only the horizontal displacement and 5 cm of the pendulum arm's length.
Make a graph showing the length of the pendulum arm squared against the average periodic time.
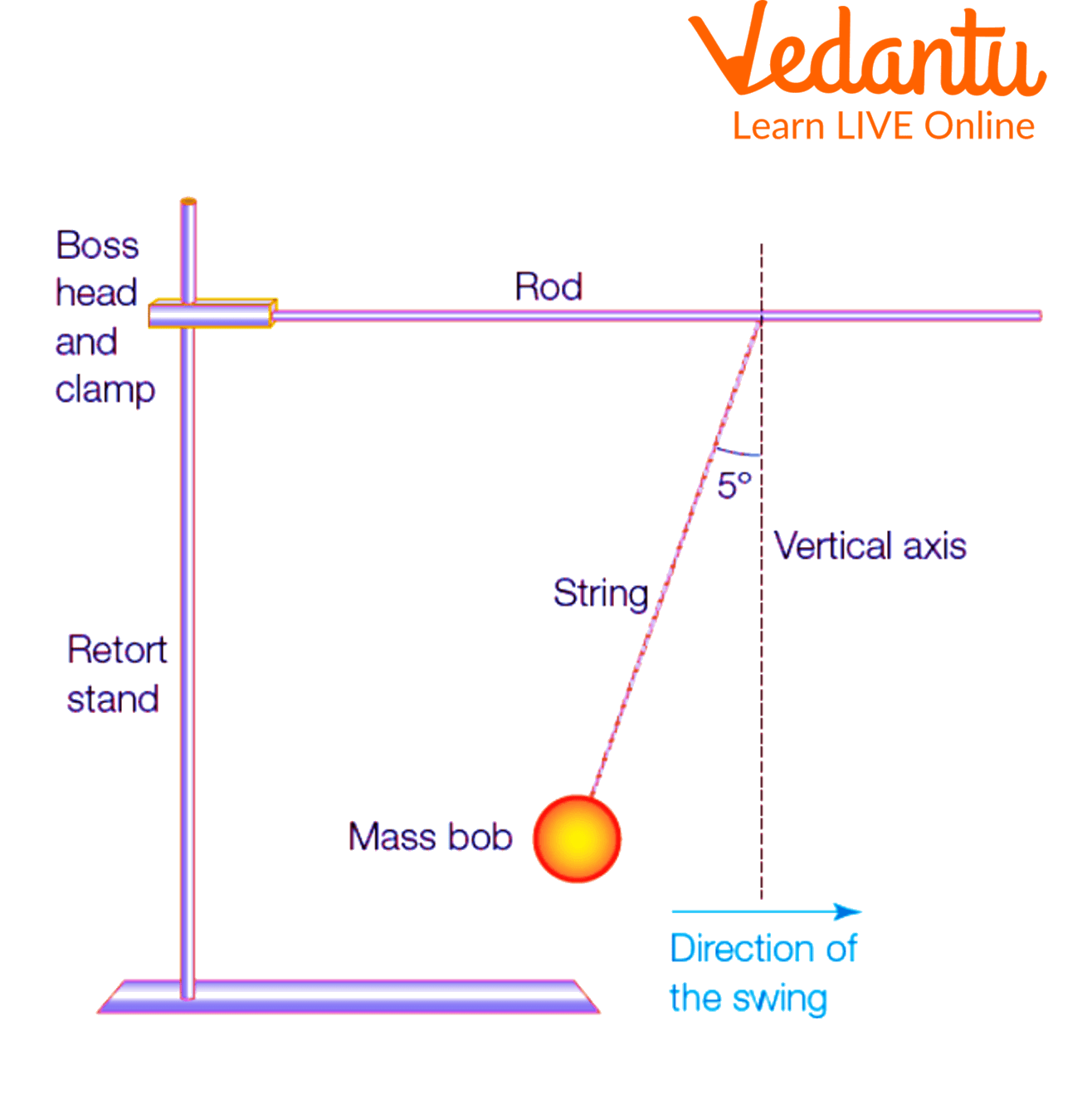
The Experimental Set-up
Observations
where\[{\rm{T = }}\dfrac{{\rm{t}}}{{{\rm{10}}}}\] and \[{\rm{g = }}\dfrac{{{\rm{4}}{{\rm{\pi }}^{\rm{2}}}{\rm{L}}}}{{{{\rm{T}}^{\rm{2}}}}}\]
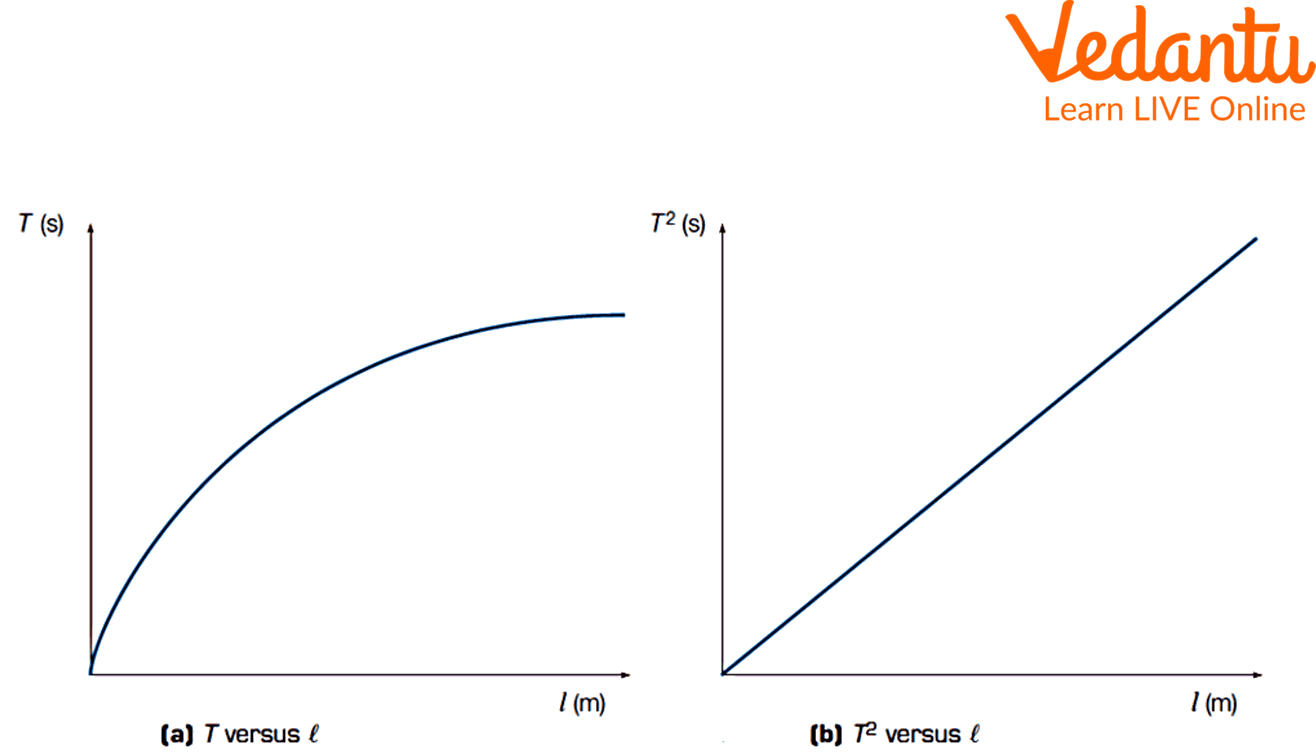
Graphical Outcomes of the L-T and L-T2 Graphs
Results
The slope is equivalent:
According to the experimental data and graph. The experimental value of the acceleration caused by gravity:
Precautions
Line up the eye with a stationary object to ensure precise timing
Reliable stop clock (decimal seconds)
Using an average of two readings to account for human error
Lab Manual Questions
1. Find at what amplitude of oscillation, the time period begins to vary.
Ans. The amplitude is independent of the period. The more amplitude, the more the distance to be covered, but the faster it will do so. The period will not change because of the interaction between distance and speed.
2. How can you determine the value of 'g', acceleration due to gravity, from the T 2 vs L graph?
Ans. The measured value of g is determined by the slope of the T2 vs. l graph of a pendulum. The equation\[{\rm{T = 2\pi }}\sqrt {\dfrac{{\rm{L}}}{{\rm{g}}}} \] determines the simple pendulum's time period T.
3. Does the time period depend on the material (density) of the pendulum bob? If yes, see the order in which the change occurs.
Ans. The length of the string solely influences a pendulum's period and not by the mass of the ball. The period of two pendulums that have the same length but have different masses will be the same. Two pendulums of various lengths will oscillate at different rates; the pendulum with the longer string will do so.
4. Does a heavier pendulum bob change the pendulum's period?
Ans. If we use a heavier bob instead of a lighter one the time period of the pendulum remains unchanged because it doesn’t depend upon the mass of the bob. It depends upon the length of the pendulum.
Viva Questions
1. Where does gravity's acceleration reach its maximum?
Ans. The square of the distance between the center and the surface determines the inverse proportionality of the acceleration caused by gravity. The equator is farther from the center than the poles are. Therefore, gravity's acceleration is greater at the poles.
2. Why can't aeroplanes be used to travel to the stars?
Ans. The minimum velocity needed to escape the earth’s gravitational pull is the escape velocity. At this speed, aeroplanes cannot fly.
3. Can a metallic wire be used in place of the thread?
Ans. Because the wire is rigid, the answer is no.
4. What does restoring force mean?
Ans. The force that pushes a vibrating body toward the mean position or a force which tries to restore the equilibrium of the pendulum.
5. At the equilibrium (mean) position, what is the net force acting on the bob?
Ans. Zero, as the tension (T) in the string completely balances the bob's weight at its average position.
6. What is equilibrium?
Ans. When a body's linear and angular accelerations are both zero, or when the net force acting on the body is zero, it is considered to be in equilibrium.
7. Can the bob be replaced with a cricket ball?
Ans. No, a simple pendulum must have bob as small as feasible by definition.
8. Where is the pendulum's length measured?
Ans. The distance between the bob's center of gravity to the point of suspension is the answer.
9. Give the following definitions: Amplitude, Vibration or oscillation, Frequency, and Time.
Ans. The greatest departure from the mean (equilibrium) position is referred to as amplitude.
Oscillation: the transition between two extreme positions followed by a return to the first.
The number of vibrations per second is known as frequency.
Time is the amount of time needed for one vibration.
10. What is simple harmonic motion?
Ans. It is a motion of the body in which the restoring force acting on the body is directly proportional to its displacement from its mean position. Still, the direction of the force is opposite to that of displacement.
Practical Based Questions
1. The value of the acceleration caused by gravity on the earth's surface at sea level is
4.9 m/s2
6 m/s2
8 m/s2
9.8 m/s2
Ans. D) 9.8 m/s2
2. A wooden ball and an iron ball with the same radius are both released into space at the same height (h). The time it took them both to get to the ground is either:
Unequal
Exactly equal
About equal
Zero
Ans. B) Exactly equal
3. What is the value of gravity's acceleration in polar regions?
Same as at the equator
More than at the equator
Less than at the equator
Zero
Ans. B) More than at the equator
4. What is an object's weight on the moon's surface equals
1/2 th of the object's weight
1/4th of the object's weight
1/6th of the object's weight
1/8th of the object's weight
Ans. C) 1/6th of the weight
5. The period of ascension from the point of projection for an object thrown vertically upward will be
Less the Time of descent
Greater the Time of descent
Equal to the Time of descent
None of the above
Ans. C) Equal to the Time of descent
6. When a body is accelerated, the force that maintains it from rotating is
Centripetal force
Magnetic force
Electrostatic force
Force of gravitation
Ans. A) Centripetal force
7. The reaction force is referred to as when it is applied to a surface in a direction perpendicular to the surface and is created by the expulsion of mass in one direction.
Weight
Pressure
Centripetal force
Thrust
Ans. D) thrust
8. The gravitational force between two objects will decrease as their separation grows if:
Decrease
Increase
Remain the same
None of the above
Ans. B) Increase
9. In a lift, a straightforward pendulum is kept swinging. If the lift descends at a constant speed, the simple pendulum's periodic period will change:
Will increase
Remains unchanged
Will lessen
Shall be 0
Ans. B) Remains unchanged
10. The simple pendulum's string tension is at its highest when the bob is:
A) In an extreme situation
B) Position that lies halfway between the average and the extreme
C) At the average position
D) Begins oscillating with extremely high amplitudes
Ans. C) At the average position
Conclusion
A basic pendulum is a mechanical device that consists of a thin, inextensible string and a small, massed bob that is designed to oscillate between the left and right extremes of its mean position. The motion can be categorized as simple harmonic motion if the bob's displacement is minimal relative to the string's length or if the displacement angle is. The time period of oscillation of the simple pendulum depends upon its length and acceleration due to gravity. And by manipulating this relation we experimentally calculated the value of acceleration due to gravity.
FAQs on Class 11 Physics Motion Under Gravity And Acceleration Due To Gravity Experiment
1. What are the three fundamental equations of motion when an object is moving vertically under the influence of gravity?
For a body moving under gravity, the acceleration 'a' is replaced by the acceleration due to gravity 'g'. The three key equations, crucial for solving most numerical problems, are:
- First Equation: v = u + gt
- Second Equation: s = ut + (1/2)gt²
- Third Equation: v² = u² + 2gs
Here, u is the initial velocity, v is the final velocity, s is the displacement, and t is the time. Remember to use a consistent sign convention (e.g., upward direction as positive and downward as negative).
2. From an exam perspective, what is the correct sign convention to use for problems involving motion under gravity?
A common mistake in exams is incorrect sign convention. For clarity and full marks, consistently follow one method. The most accepted convention as per the CBSE syllabus is:
- Any vector quantity directed upwards (like initial velocity for an object thrown up) is taken as positive.
- Any vector quantity directed downwards (like displacement when an object falls back to the ground) is taken as negative.
- Acceleration due to gravity (g) always acts downwards, so it is almost always taken as -g (approximately -9.8 m/s²).
3. Explain why a feather and a bowling ball fall with the same acceleration in a vacuum. Why is this an important concept?
This is a frequently asked conceptual question. In a vacuum, there is no air resistance. The acceleration of a falling object is the acceleration due to gravity (g), which is independent of the object's mass, shape, or size. The gravitational force (F = GmM/R²) is greater on the bowling ball, but its inertia (mass) is also greater. According to Newton's second law (a = F/m), the larger force on the bowling ball is cancelled out by its larger mass, resulting in the same acceleration 'g' for both objects. This is important because it demonstrates that gravity accelerates all objects equally, a cornerstone of physics.
4. A ball is thrown vertically upwards. At its highest point, its velocity is zero. Is its acceleration also zero? Justify your answer.
No, its acceleration is not zero. This is a classic Higher Order Thinking Skills (HOTS) question. At the highest point, the ball momentarily stops, so its instantaneous velocity is zero. However, the force of gravity is still acting on it, pulling it downwards. Since there is a net downward force, the ball has a constant downward acceleration equal to 'g' (approximately 9.8 m/s²) throughout its entire flight, including at the very peak.
5. What are the key factors that cause the value of acceleration due to gravity (g) to vary on Earth?
The value of 'g' is not constant everywhere. For a 2 or 3-mark question, you should mention these important factors:
- Altitude: 'g' decreases as you move away from the Earth's surface (increase in height or altitude).
- Depth: 'g' also decreases as you go down from the Earth's surface towards its centre. It is maximum at the surface.
- Shape of the Earth: The Earth is not a perfect sphere; it is flattened at the poles and bulged at the equator. Since the equatorial radius is larger than the polar radius, the value of 'g' is slightly less at the equator and more at the poles.
6. How would you structure the solution for a typical 3-mark numerical where a stone is dropped from a tower of height 100 m, and you need to find the time taken to reach the ground?
To solve this important type of numerical and score full marks, follow these steps:
- List the knowns: Initial velocity (u) = 0 (since it's dropped), Displacement (s) = -100 m (downwards), Acceleration (a) = -g ≈ -9.8 m/s².
- Identify the unknown: Time (t).
- Select the correct equation: The equation relating s, u, a, and t is s = ut + (1/2)at².
- Substitute and solve: -100 = (0)t + (1/2)(-9.8)t². This simplifies to -100 = -4.9t². Solving for t gives t ≈ 4.52 seconds.
- State the final answer: Clearly write the final answer with the correct units, e.g., 'The time taken to reach the ground is 4.52 s.'
7. Compare the time of ascent and time of descent for a body projected vertically upwards. Under what condition are they not equal?
In an ideal scenario, neglecting air resistance, the time of ascent is exactly equal to the time of descent. This is because the acceleration remains constant ('g') throughout the motion. The speed at which it is projected upwards is the same as the speed with which it returns to the point of projection. However, in real-world conditions where air resistance is considered, the time of descent is greater than the time of ascent. This is because air resistance opposes the motion, reducing the net upward acceleration during ascent and reducing the net downward acceleration during descent, thus taking longer to fall.
8. How is the concept of 'motion under gravity' a special case of projectile motion? Explain the independence of motion components.
Motion under gravity (a body moving vertically) is a one-dimensional special case of projectile motion. In general projectile motion, an object has two components of velocity:
- Horizontal Motion: In the absence of air resistance, there is no horizontal force. This means the horizontal acceleration is zero, and the horizontal velocity remains constant.
- Vertical Motion: This component is governed solely by gravity. The vertical acceleration is always 'g' downwards, and the vertical velocity changes continuously.
This principle of independence of motion is crucial: the vertical motion due to gravity has no effect on the horizontal motion, and vice versa. This allows us to analyse the two components separately to solve projectile problems.
9. How does the apparent weight of a person in a lift change when it is (a) accelerating upwards and (b) in free fall?
This is an important application-based question. Apparent weight is the normal reaction force (R). The actual weight is mg.
- (a) Accelerating Upwards: When the lift accelerates up with 'a', the net force is R - mg = ma. Therefore, the apparent weight is R = mg + ma. The person feels heavier.
- (b) In Free Fall: Free fall occurs when the lift's cable breaks and it accelerates downwards with 'g'. The net force is mg - R = mg. This gives an apparent weight R = 0. This is the condition of weightlessness.
10. What is escape velocity, and how is it related to motion under gravity?
Escape velocity is the minimum velocity an object must have to escape the Earth's gravitational field completely and never return. It is related to motion under gravity because it represents the speed needed to overcome the continuous downward pull of gravity. For Earth, its value is approximately 11.2 km/s. While standard motion under gravity problems deal with objects that return to Earth, escape velocity defines the threshold for an object to break free from this gravitational confinement.
























