Class 11 Physics Measurement Using Vernier Callipers Experiment

Measurement is an integral part of our life. Several times the ordinary tools required for measurement are not precise enough for our needs. As physics students, this becomes a great issue for most of us while working in our laboratories. In such cases, where there arises a need to measure smaller distances, a vernier calliper comes as a handy tool. 

In daily life, we need to measure the precise dimensions of iron rods in construction, adjustment of pipe fittings in households, drilling tools, etc. In each of these, we usually need vernier callipers to precisely determine the dimensions and minimise the uncertainties.

In this experiment, we will learn how to measure linear distances using vernier callipers. We'll be estimating the dimensions of a solid cube of known mass to estimate its mass density as an application of the same.

Table of Contents

• Aim

• Apparatus Required

• Theory

• Procedure

• Observations

• Result

• Lab Manual Questions

• Viva Questions

• Practical Based Question

• Conclusion

Aim

To measure the dimensions of a small solid cube of known mass using vernier callipers and hence to estimate its mass density.

Apparatus Required

• A vernier callipers

• A given small solid cube of known mass

• Magnifying lens

Theory

A vernier calliper is a measuring scale used to measure smaller distances than a centimetre scale. It is equipped with a main centimetre scale and a small vernier scale sliding over it. Vernier constant is defined as the difference between the values of one main scale and one vernier scale division. 

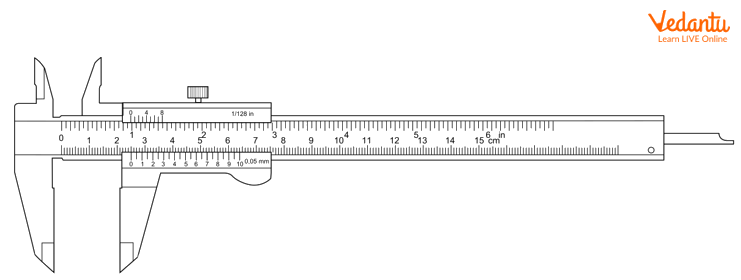
Vernier Callipers

To get the least count of vernier scale, slide the smaller scale towards the fixed end so that both the teeth are in contact. Observe the small scale using a magnifying lens. If MSD refers to one Main Scale Division and VSD refers to one Vernier Scale Division, then:

\[10\;VSD = 9\;MSD\]

\[\Rightarrow 1\;VSD = \dfrac{9}{{10}}MSD = 0.9\;MSD\]

Least Count \[LC\] or Vernier Constant,

\[LC = 1\;MSD - 1\;VSD\]

\[\Rightarrow LC = 1\;MSD - 0.9\;MSD\]

\[\Rightarrow  LC= 0.1\;MSD\]

Since 1 MSD =\[0.1\;cm\], hence

\[LC = 0.1 \times 0.1\;cm = 0.01\;cm\]

\[\Rightarrow LC = 0.01 \times 10\;mm\]

\[\Rightarrow LC = 0.1\;mm\]

Hence, the least count or vernier constant of a vernier scale is 0.1 mm, ten times smaller than that of a conventional centimetre scale.

In this experiment, we are going to precisely measure the linear dimensions of a solid cube using vernier callipers and estimate its mass density using volume and known mass.

Procedure

1. Slide the smaller scale to the fixed end so that both teeth of the instrument touch each other. Check that the zero of the vernier scale coincides with that of the main scale.

2. If they do not coincide, note the MSD with which zero of vernier scale coincides.

3. Place the object between the two teeth of the instrument. Note the MSD with which the zero of vernier scale coincides or which is immediately before the zero of vernier scale using magnifying glass. This is the Main Scale Reading \[MSR\].

4. Note the VSD which is nearly perfectly coinciding with any of the MSD. This is the Vernier Scale Reading \[VSR\].

5. Take three such readings for MSR and VSR for length of the cube.

6. In the same way, take three MSR and VSR readings each for the breadth and height of the cube. Tabulate the observations.

Observations

We will note down three MSR and VSR each for three material dimensions. Then we will take the average each for length, breadth and height to get the precise result.

Observation Table

Least count \[LC\] = 0.01 cm

Result

Reading = \[MSR + (LC \times VSR)\] = ………………

\[\text{Average} = \dfrac{\text{Sum of all readings}}{\text{Number of readings}}\] = …………

\[Volume = (Average\;length) \times (Average\;breadth) \times (Average\;height)\;c{m^3}\] = ……………

\[\text{Mass density} = \dfrac{\text{Given mass}}{\text{Determined volume}}\] = ……………..

Precautions

1. Always add/ subtract the zero error in the final reading.

2. Ensure that the vernier scale slides smoothly over the main scale.

3. Note the coinciding divisions very carefully using magnifying lens.

Lab Manual Questions

1. How can you find the thickness of the steel sheet used to make the tumbler using vernier callipers?

Ans: For measuring the thickness of the steel sheet, first measure the inner diameter of the tumbler, and then the outer diameter of the tumbler using the vernier callipers. Then the thickness of the sheet can be calculated by subtracting the inner diameter from the outer diameter and then dividing it by 2.

2. How the precision of an instrument will change if one will change when changing the number of divisions on the vernier callipers?

Ans: If the number of divisions on the vernier callipers will change then it will eventually decrease the precision of the instrument. Since the least count of the vernier callipers is defined as the, Least Count (LC) = 1 MSD-1VSD, so in ideal gas, 1 main scale, which is 1 mm,  will be equal to the 10 VSD of 9 mm, and then LC = 0.1 mm, so if now we increase VSD to 20 instead of 10 then for such case the LC will be equal to 1 mm -0.45 mm = 0.55 mm, and therefore, precision will decrease.

3. In the vernier scale (angular) normally provided in spectrometers/sextant, 60 VSD coincides with 59 MSD (each division of angle 1°). Find the least count of the vernier.

Ans: In the vernier scale of spectrometers, the least count is defined as:

\[LC = 1\;MSD - 1\;VSD\]

In the given problem, we have

\[60\;VSD = 59\;MSD\]

\[ \Rightarrow 1\;VSD = \dfrac{{59}}{{60}}\;MSD\]

Therefore                                 

\[LC = 1\;MSD - \dfrac{{59}}{{60}}\;MSD\]

\[ \Rightarrow LC = \dfrac{{60 - 59}}{{60}}MSD\]

\[ \Rightarrow LC = \dfrac{1}{{60}}MSD\]

\[ \Rightarrow LC = \;1'\]

Thus, the least count is 1’.

4. How can you find the value of π using a given cylinder and a pair of vernier callipers? 

Ans: Take a metal sheet and make a cylinder out of it, now measure the diameter D of the cylinder using the vernier callipers and then measure the circumference of the cylinder, which is length of the sheet L with a conventional metre scale. Now calculate the ratio of the L and D results, which gives you the value of π.

Viva Questions

1. What is a vernier calliper?

Ans: A vernier calliper is a simple instrument used for accurately measuring lengths up to 0.1 mm.

2. Which is larger, MSD or VSD?

Ans: MSD is larger than VSD.

3. How will the accuracy be affected if VSD increases?

Ans: As VSD increases, least count decreases and hence accuracy increases.

4. How will you determine the least count of a vernier scale?

Ans: The least count of the vernier scale is given by the ratio of smallest division of main scale to the total number of divisions on vernier scale.

5. What is zero error?

Ans: When the zeroes of the main scale and vernier scale do not coincide, the error arising in calculation is known as zero error.

6. How will you find corrected reading?

Ans: Corrected reading is given by adding or subtracting the zero error in calculated reading.

7. How does temperature affect reading?

Ans: As the temperature increases, the length expands. Hence, reading increases.

8. What are teeth and sharp straps used for?

Ans: Teeth are used for measuring inner and outer diameters and the strap is used for measuring the depth of a container.

9. How do you define the vernier constant?

Ans: Vernier constant is defined as the least count of vernier callipers. Its value is 0.01 cm.

9. How do you calculate the measurement of a length using vernier callipers?

Ans: The length is measured by adding the main scale reading to the least count times the vernier scale reading.

Practical Based Questions

1. The least count of vernier callipers is:

1. 1 mm

2. 0.1 mm

3. 0.01 mm

4. 0.001 mm

Ans: B) 0.1 mm

The least count of vernier callipers is 0.1 mm.

2. How many scales does a vernier calliper have?

1. 1

2. 2

3. 3

4. 4

Ans: B) 2

A vernier calliper has 2 scales.

3. A vernier callipers is accurately used to measure:

1. Length

2. Area

3. Volume

4. Time

Ans: A) Length

A vernier calliper is accurately used to measure length.

4. How many sets of jaws does a vernier calliper have?

1. 1

2. 2

3. 3

4. 4

Ans: B) 2

A vernier calliper has 2 sets of jaws.

5. Vernier constant is given by:

1. MSD + VSD

2. MSD - VSD

3. MSD × VSD

4. MSD ÷ VSD

Ans: B) MSD - VSD

Vernier constant is given by MSD - VSD.

6. The reading is calculated by:

1. MSD + LC × VSD

2. MSD - LC × VSD

3. VSD + LC × MSD

4. VSD + LC × MSD

Ans: A) MSD + LC × VSD

The reading is calculated by MSD + LC × VSD.

7. The number of MSD that coincide with 10 VSD are:

1. 7

2. 8

3. 9

4. 10

Ans: D) 10

9 MSD coincides with 10 VSD.

8. Vernier calliper does not finds applications in:

1. Laboratories

2. Industries

3. Time-keeping

4. Medicine

Ans: C)Time-keeping

Vernier calliper does not find applications in time-keeping.

9. Using the vernier callipers on a body with known mass, one can calculate its:

1. Mass density

2. Number density

3. Viscosity

4. Elasticity

Ans: A) mass density.

Using this data, one can calculate its mass density.

10. The number of divisions on vernier scale are:

1. 5

2. 10

3. 15

4. 20

Ans: B) 10

The number of divisions on the vernier scale are 10.

Conclusion

From this experiment, we can say that the instrument vernier callipers find an immense use in measurement over the conventional centimetre scales for measuring linear distances. Due to their least count about one-tenth of that of ordinary scale, they provide up to ten times the precision for measuring. We hope that, after this experiment, the reader has got some useful insight in the concept of vernier callipers, its diagram, theory, working formula and practical applications.