




An Overview of Class 11 Physics Atmospheric Pressure Experiment
Study of atmospheric pressure carries an essential significance for us. Atmospheric pressure helps us to estimate the suitable weather conditions prevailing over an area – a low-pressure system leads to precipitation, cloudiness and wind, whereas a high-pressure system leads to calm and fair weather. A small change in atmospheric pressure leads to a change in health conditions among humans, such as change in blood pressure and uneasiness. Following is a simple experiment, intended to give the reader an insight of a simple apparatus to measure atmospheric pressure.
Table of Contents
Aim
Theory
Procedure
Observations
Result
Aim
To measure the atmospheric pressure using Fortin’s barometer.
Apparatus Required
Fortin’s barometer
Thin safety gloves
Thermometer
A paper and pencil
Theory
Fortin’s barometer consists of a vertical glass tube of about a meter, opened at the downward end into a beaker labelled C. The tube is filled with mercury up to a certain limit put into the beaker containing mercury. Leather patch L closes the side and a small ivory pin P touches the level of mercury in the beaker at its tip for adjusting zero of the scale in accordance with the mercury level. A graduated scale is engraved on the outer tube.
There exists a vacuum at the top as some mercury spills down from the tube into the beaker due to gravity. Mercury level stabilizes when the pressure exerted by the mercury in the tube is equal to the atmospheric pressure exerted in the beaker. At this point, from the graduated scale, we can determine the atmospheric pressure by noting the mercury level and the formula
\[P = h\rho g\]
where P = Pressure exerted by the mercury column under stable condition = Atmospheric pressure
h = Height of the mercury column
\[\rho \]= Density of mercury =\[13600\;kg/{m^3}\]
g = Acceleration due to gravity =\[9.8\;m/{s^2}\]
By noting three observations at different temperatures, the atmospheric pressure can be determined.
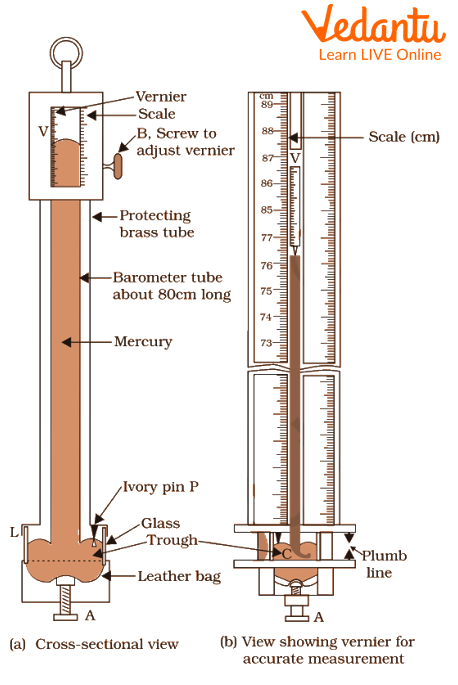
Barometer
Procedure
Hang the barometer vertically on a wall using a plumb line.
Check all the screws and least count of the engraved scale.
Adjust the level of mercury in the tube. Ensure that the tip of the ivory pointer P exactly touches the surface of mercury in the beaker (see below figure).
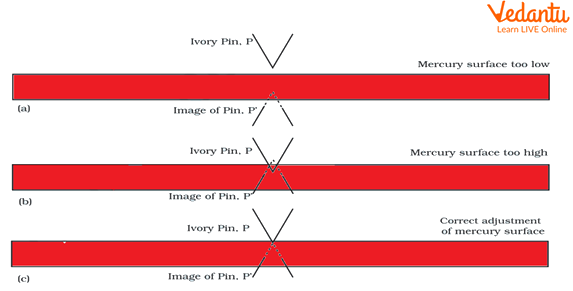
Mercury Surface in the Reservoir.
Procedure of Seeing the Level of Meniscus.
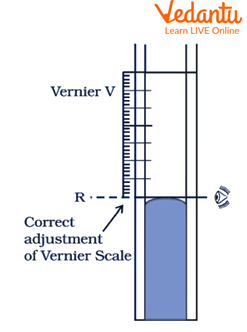
Adjust the smaller scale such that its zero exactly touches the convex meniscus of the mercury in the tube. The convex meniscus should be the level to be observed.
Allow the mercury level to stabilize for 5 minutes. Note the readings on both scales. Also note the temperature, date and time.
Repeat the same procedure two more times (in the interval of some days) such that the temperature changes. Tabulate the data.
Observations
Divisions on main scale = ..........
Least count of main scale = ..........
Divisions on vernier scale = ..........
Least count (LC) of vernier scale = ..........
Room temperature = ..........\[^\circ C\]
Observation Table
Result
At temperature\[{T_1}\], atmospheric pressure\[{P_1}\]= ............ \[(N/{m^2})\]
At temperature\[{T_2}\], atmospheric pressure\[{P_2}\]= ............ \[(N/{m^2})\]
At temperature\[{T_3}\], atmospheric pressure\[{P_3}\]= ............ \[(N/{m^2})\]
Precautions
Handle the barometer very carefully while hanging on the wall.
The wall mount should be rigid.
Note the least count and readings of both the scales very carefully.
Screws should be handled with due care.
Temperature differences should be finite but not very small/ very large.
Lab Manual Questions
1. Why is the barometer required to be adjusted every time before use?
Ans: Various pressures can vary the accuracy of mobile signals and bounce-off walls. They also changed due to altitude. To remove this residual pressure error, the barometer requires to be adjusted every time before use.
2. What will happen to the readings if the ivory pin is not adjusted properly?
Ans: Ivory pin adjusts the zero of the scale at the same level as that of mercury in the beaker. If not adjusted properly, the zero of the scale will not be adjusted and we may record an incorrect height of the mercury column.
3. Why should the tube be perfectly erect and not tilted?
Ans: If the mercury tube gets tilted, the pressure exerted by the mercury column in the tube will not be the actual pressure, but only a component of it depending upon the angle of tilt. So, the observer will not be able to measure correct atmospheric pressure from the graduated scale.
4. Can we use water in place of mercury? Why/ Why not?
Ans: From a theoretical point of view, any liquid can be used in a barometer. But practically, mercury is much denser than water, leading the tube height in a convenient zone. By contrast, the tube height in the case of water would be over 10 meters.
Viva Questions
1. What is atmospheric pressure?
Ans: Atmospheric pressure refers to the weight per unit area exerted by the air column on the surfaces beneath it due to the action of gravity. This is because air particles have a finite mass and hence get attracted by the gravitational force of the earth.
2. Give the atmospheric pressure formula. What is the unit of atmospheric pressure?
Ans: Atmospheric pressure is given by the formula
\[P = h\rho g\]
where
P = Pressure exerted by the mercury column under stable condition = Atmospheric pressure
h = Height of the mercury column
\[\rho \]= Density of mercury =\[13600\;kg/{m^3}\]
g = Acceleration due to gravity =\[9.8\;m/{s^2}\]
The SI unit of atmospheric pressure is newtons per square meter (\[N{m^{ - 2}}\]) or Pascal (Pa).
3. Explain the three types of pressure.
Ans: The three types of pressure are:
Absolute pressure: Pressure having a reference of perfect vacuum is called absolute pressure.
Gauge pressure: Pressure having a reference of atmospheric pressure is called gauge pressure.
Vacuum pressure: Pressure below atmospheric pressure is known as vacuum pressure.
Absolute pressure is the sum of vacuum and gauge pressures.
4. State the relationship between different pressure units.
Ans: Relationship between different pressure units are as follows:
1 atm = 14.6956 psi = 760 torr
1 bar = 750.0623 torr = 0.98696 atm = 100000 pascal
1 pascal = 10 \[dyne/c{m^2}\]
1 \[kg/c{m^2}\] = 14.696 psi = 10000 mm \[{H_2}O\]
5. What is a manometer? Explain its working.
Ans: A manometer is an instrument used to measure differential pressure using a U-tube filled with liquid, whose both ends are connected to pipe/ pressure tapings. There exists a difference in heights of the liquid in both the tubes of the U-tube due to a difference in pressure, which is readily noted.
6. What is a strain gauge?
Ans: A strain gauge is a resistive element, whose shape changes on the application of pressure which is directly proportional to the pressure applied.
7. Name the most common type of pressure measuring device used in industries.
Ans: Most common type of pressure measuring device used in industries is capacitive-type pressure transmitter.
8. Name five important measuring devices used in industries.
Ans: Important devices used in industries are:
Pressure gauge
Manometer
Resistance type pressure measurement
Capacitive type pressure measurement
Inductive type pressure measurement
9. What causes pressure in the atmosphere?
Ans: Atmospheric pressure is created by various layers of atoms and molecules that make up the atmosphere. They constantly move in random directions and strike upon a surface to generate atmospheric pressure.
10. Give some useful atmospheric pressure examples.
Ans: Atmospheric pressure examples include:
Rubber sucker
Drinking straw
Syringe and dropper
Practical Based Questions
1. Divers wear special suits to get protection from:
Low pressure
Low temperature
High pressure
High temperature
Ans: (C) Divers wear special suits to get protection from combined high pressure due to atmosphere and water.
2. Air pressure is ............ as that at the sea lever at high altitudes.
Same
Less than
More than
Depends on region
Ans: (B) At higher altitudes, air pressure is less than the pressure at sea level.
3. The atmospheric pressure at the sea level is ............ atm.
1
10
100
1000
Ans: (A) The atmospheric pressure at the sea level is 1 atm.
4. Pressure increases with:
Increasing depth
Decreasing depth
Tangential to the depth
Depends on temperature
Ans: (A) Pressure increases with an increase in depth.
5. Atmospheric pressure is measured by an instrument called:
Seismograph
Compass
Anemometer
Barometer
Ans: (D) Atmospheric pressure is measured by an instrument called a barometer.
6. Atmospheric pressure is maximum at:
Top of a building
Sea level
About 1 km below the surface of sea level
None of these
Ans: (B) Atmospheric pressure is maximum at sea level because at the sea level, air molecules are compressed by weight above them at the most.
7. Why does a nail have a pointed tip?
Force acting on small area exerts small pressure
Force acting on large area exerts zero pressure
Force acting on small area exerts large pressure
Force acting on large area exerts large pressure
Ans: (C) A nail has a pointed tip so that the force acting on a small exerts a large pressure.
8. One atmospheric pressure is equal to:
100 Pa
1000 Pa
100000 Pa
10000000 Pa
Ans: (C) One atmospheric pressure is equal to 100000 Pa.
9. Gas pressure is caused due to:
Gas molecules colliding with one another
Gas molecules colliding with the walls of the container
Heating of gas molecules
Gas molecules reacting with each other
Ans (B) Gas pressure is caused due to the molecules colliding with the walls of the container.
10. What is the thrust on a unit area called?
Volume
Surface area
Mass density
Pressure
Ans: (D) The thrust on a unit area is called pressure.
Conclusion
From this experiment, we can conclude that the study of various kinds of pressures, particularly atmospheric pressure, is indispensable in the field of physics for us. A check on atmospheric pressure helps us to determine prevailing weather conditions over a region. Similarly, changing pressure conditions changes the health balance in human beings. Pressure is commercially essential in many of our daily services and a number of creative instruments exist to keep a check on pressure.
FAQs on Class 11 Physics Atmospheric Pressure Experiment
1. What is atmospheric pressure and what is its standard value at sea level in different units?
Atmospheric pressure is the pressure exerted by the weight of the air in the Earth's atmosphere. At sea level, the standard atmospheric pressure is considered to be 1 atmosphere (atm). This is an important value for solving many physics problems. It is equivalent to:
- 1.013 × 10⁵ Pa (Pascals or N/m²)
- 760 mm of Hg (millimetres of mercury)
- 76 cm of Hg
- 10.3 m of water
2. State Pascal's law and mention two important applications that are frequently asked in exams.
Pascal's law states that a pressure change at any point in a confined incompressible fluid is transmitted throughout the fluid such that the same change occurs everywhere. This is a crucial principle in fluid mechanics for Class 11. Two important applications based on this law are:
- Hydraulic Lift: Used to lift heavy objects like cars. A small force applied on a piston with a small area generates a large force on a piston with a larger area, as pressure (F/A) is transmitted equally.
- Hydraulic Brakes: Used in automobiles. The force applied by the driver's foot on the brake pedal is transmitted through the brake fluid to the brake shoes, stopping the vehicle.
3. As per the CBSE 2025-26 syllabus, derive the expression for pressure at a depth 'h' below the surface of a liquid.
To derive the expression for pressure variation with depth, consider a cylindrical element of liquid of height 'h' and cross-sectional area 'A'. The liquid is at rest. The forces acting on the cylinder are:
- Force on the top surface due to atmospheric pressure: F₁ = PₐA (downwards)
- Weight of the liquid cylinder: W = mg = (Ahρ)g (downwards), where ρ is the density of the liquid.
- Force on the bottom surface due to the liquid below it: F₂ = PA (upwards)
For the cylinder to be in equilibrium, the upward force must balance the downward forces: F₂ = F₁ + W. Substituting the values:
PA = PₐA + (Ahρ)g
Dividing by A, we get the important expression: P = Pₐ + hρg. This shows that pressure increases linearly with depth.
4. Explain why a mercury barometer is used to measure atmospheric pressure and why mercury is a more suitable liquid than water.
A mercury barometer works by balancing the atmospheric pressure against the pressure exerted by a column of mercury in an inverted tube. The height of this mercury column indicates the atmospheric pressure. Mercury is the preferred liquid for a barometer for several important reasons:
- High Density: Mercury is about 13.6 times denser than water. This means the column needed to balance atmospheric pressure is only about 76 cm high, which is a convenient size. A water barometer would need to be over 10 metres tall, which is impractical.
- Low Vapour Pressure: Mercury has a very low vapour pressure at room temperature, so the space above the column (Torricellian vacuum) is nearly a perfect vacuum, ensuring an accurate reading.
- Non-stick Property: Mercury does not stick to the glass tube, which allows for a clear and accurate measurement of the column's height.
5. What is gauge pressure and absolute pressure? How are these two important pressure measurements related?
Understanding the difference between gauge and absolute pressure is essential for solving numericals.
- Absolute Pressure: It is the total pressure measured relative to a perfect vacuum (zero pressure). It accounts for the atmospheric pressure acting on a system.
- Gauge Pressure: It is the pressure measured relative to the local atmospheric pressure. It is the difference between the absolute pressure and the atmospheric pressure. Most pressure gauges, like a car tyre gauge, measure this value.
The relationship between them is given by the formula: P_absolute = P_gauge + P_atmospheric. Gauge pressure can be positive (if absolute pressure > atmospheric pressure) or negative (if absolute pressure < atmospheric pressure).
6. Explain why a person is not crushed by the immense atmospheric pressure acting on their body.
This is a high-order thinking question (HOTS). We are not crushed by atmospheric pressure because the pressure inside our bodies is almost equal to the external atmospheric pressure. The fluids in our body, particularly our blood, exert an outward pressure that effectively balances the inward pressure from the atmosphere. This internal pressure prevents our bodies from collapsing under the approximately 1,00,000 Newtons of force exerted on us by the air.
7. A hydraulic lift is designed to lift a car of mass 2000 kg. The area of the cross-section of the piston carrying the car is 500 cm². What is the maximum pressure the smaller piston would have to bear?
This is a typical important numerical based on Pascal's Law.
First, calculate the force exerted by the car on the larger piston (weight of the car):
Force (F₂) = mass (m) × acceleration due to gravity (g)
F₂ = 2000 kg × 9.8 m/s² = 19600 N
Next, convert the area of the larger piston to m²:
Area (A₂) = 500 cm² = 500 × 10⁻⁴ m² = 0.05 m²
Now, calculate the pressure on the larger piston:
Pressure (P₂) = F₂ / A₂
P₂ = 19600 N / 0.05 m² = 392,000 Pa or 3.92 × 10⁵ Pa.
According to Pascal's law, this pressure is transmitted equally throughout the fluid. Therefore, the maximum pressure the smaller piston would have to bear is also 3.92 × 10⁵ Pa.
8. How do everyday actions like using a drinking straw or filling a syringe demonstrate the principle of atmospheric pressure?
These actions are excellent real-world examples of atmospheric pressure at work:
- Drinking Straw: When you suck on a straw, you reduce the air pressure inside it. The higher atmospheric pressure outside the straw then pushes the liquid up into the straw and into your mouth. You are not 'pulling' the liquid up; the atmosphere is 'pushing' it.
- Syringe: When the plunger of a syringe is pulled back, it creates a region of low pressure inside the barrel. If the tip of the syringe is in a liquid, the greater atmospheric pressure on the surface of the liquid pushes it into the barrel until the pressure inside equalises.
9. What would happen to the reading of a mercury barometer if it were taken inside a commercial airplane flying at 30,000 feet? Justify this important conceptual scenario.
This is a common conceptual trap. While the atmospheric pressure outside the airplane at 30,000 feet is very low, the inside of the cabin is pressurised to a level equivalent to the pressure at about 6,000-8,000 feet. Therefore, the barometer would not show the extremely low pressure of the high altitude. Instead, it would show the artificially maintained cabin pressure, which is significantly higher than the outside pressure but still lower than the standard sea-level pressure. The reading would be lower than 76 cm of Hg, but much higher than what it would be if exposed to the outside air.
















