Maths Notes for Chapter 13 Visualising Solid Shapes Class 7 - FREE PDF Download
Plane Figures and Solid Shapes:
Plane figures are flat or $2$-Dimension figures, they have no thickness.
For example: Squares, rectangles, circles, triangles etc.
Solid Shapes are $3$-Dimension shapes, and they occupy space and have volume.
For example: Cube, cuboid, sphere, cone, hemisphere etc.
Faces, Edges and Vertices of $3D$ Shapes:
A $3D$ shapes is not flat therefore it has $3$ dimensions and these are faces, edges, and vertices.
Faces: It is simply the face of a $3D$ shape or the flat surface of the $3D$ shape
For example: The number of faces of a cube is $6$.
Edges: They are the line segments which join one vertex to another vertex.
For example – Edges in a cylinder are $2$ and are shown below.
Vertices: Points where two or more edges meet between faces are known vertices of any $3D$ shape or the corners of $3D$ shape.
For example: The cube has $8$ vertices and is shown below
Net for building $3D$ Shapes:
Net is used for making $3D$ shapes.
It is a basic skeleton outline in $2$-Dimensions i.e., it is a flat $3$-Dimensional shape which can be folded and joined together with the help of glue.
Nets for building some shapes are shown below
Drawing Solids on a Flat Surface:
There are two ways of drawing solids on a flat surface
Oblique Sketches:
It is an easy way of representing the $3D$ objects in pictorial form.
These sketches are intended to show the perspective of $3D$ object and are drawn on a sheet by freehand.
It does not talk about the measurement of $3D$ object
Oblique sketch of cube is shown below
Isometric Sketches:
It is also the pictorial representation of a $3D$ objects, but it also meets with measurements of the $3D$ object to be drawn.
It is drawn on isometric sheets.
Isometric sketch of cube is shown below and the dotted sheet on which the sketch is made is known as isometric sheet
Viewing Different Sections of a Solid
There are many methods to view different sections of a solid.
Slicing and Cutting: It gives the cross-sectional view of a solid.
Shadow Casting: It gives $2D$ view of an $3D$ object.
Viewing Solid from Different Angle: The front-view, the side-view and the top-view are the most common ways to view a solid; it can provide a lot of information about the shape.
For example: The different view of a building is shown below
Chapter Summary - Visualising Solid Shapes
"Visualising Solid Shapes," Class 7 Maths, unveils the magic of three-dimensional wonders. From cubes to cones, this chapter invites students to explore and understand the secrets of solid shapes. Concepts like edges, vertices, and faces come to life as students embark on a journey to visualise and recognise these shapes in everyday objects. Through simple explanations and relatable examples, the chapter transforms abstract geometry into tangible knowledge. As students delve into the world of "Visualising Solid Shapes," they discover the beauty of spatial thinking, making learning a captivating adventure into the realm of cubes, spheres, and the geometry that surrounds us.
What are the Benefits of Referring to Vedantu’s Revision Notes for Class 7 Maths Chapter 13 - Visualising Solid Shapes?
Embark on a visual journey with Vedantu’s Revision Notes for Class 7 Maths Chapter 13 - Visualising Solid Shapes. These notes are your passport to unlocking the secrets of three-dimensional wonders, making complex geometry as easy as counting cubes. Let's explore the benefits these notes bring to your learning adventure!
1. Concept Summaries: Quickly grasp the secrets of visualising solid shapes, turning complex concepts into clear, tangible insights.
2. Simplified Understanding: Navigate through the complexities of spatial geometry effortlessly, transforming abstract shapes into relatable knowledge.
3. Last-Minute Mastery: Revision Notes are a handy resourcel for last-minute exam preparations, ensuring you're well-versed in visualising solid shapes and their properties.
4. Enhanced Memory Retention: Solidify your understanding of crucial information, reinforcing it for long-term memory.
5. Strategic Exam Preparation: Guiding you with key points and tips specific to visualising solid shapes, ensuring you're well-prepared for your exams.
6. Time-Efficient Learning: Save time by accessing consolidated information, allowing you to focus on mastering the intricacies of solid shapes efficiently.
7. Focused Prioritization: Recognize the importance of specific topics and questions related to visualising solid shapes, giving you a targeted approach to your studies.
8. Real-World Connections: Understand the practical applications of solid shapes with examples connecting the abstract concepts to the real world.
9. Confidence-Boosting Study Aid: Approach your exams with confidence, knowing Vedantu's notes serve as a reliable companion in your journey to mastering visualising solid shapes.
Conclusion
For an enhanced comprehension of this subject, NCERT - Class 7 Maths Chapter 13 - Visualising Solid Shapes, thoughtfully prepared by experienced educators at Vedantu, is your invaluable companion. These notes break down the complexities of Visualising Solid Shapes into easily digestible sections, helping you grasp new concepts, master formulas, and navigate through questions effortlessly and quickly at the last minute as well. By immersing yourself in these notes, you not only prepare for your studies more efficiently but also develop a profound understanding of the subject matter.
Related Study Materials for Class 7 Maths Chapter 13 Visualising Solid Shapes
Chapter-wise Links for Class 7 Maths Notes
Important Study Materials for Class 7 Maths
FAQs on Visualising Solid Shapes Class 7 Maths Chapter 13 CBSE Notes - 2025-26
1. What are the key concepts to cover in a quick revision of Class 7 Maths Chapter 13, Visualising Solid Shapes?
For a quick revision of this chapter, you should focus on the core concepts. Start with the fundamental difference between 2D and 3D shapes. Then, cover the components of solid shapes, including faces, edges, and vertices. Also, revise the concept of nets for building 3D shapes, methods for drawing solids like oblique and isometric sketches, and how to visualise different views (top, front, and side) of a solid object.
2. How can you quickly differentiate between a 2D plane shape and a 3D solid shape during revision?
The quickest way to differentiate is by their dimensions. Plane shapes, such as squares or circles, are two-dimensional (2D) because they only possess length and breadth. In contrast, solid shapes, like cubes or spheres, are three-dimensional (3D) as they have length, breadth, and height, which gives them volume and depth.
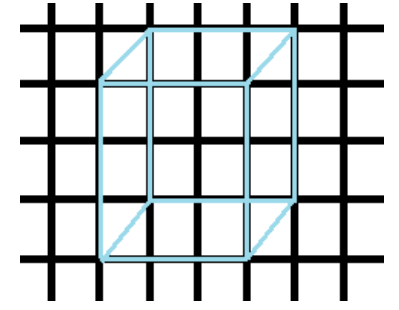
3. What is the main difference between an oblique sketch and an isometric sketch?
Both are methods for representing 3D shapes on a 2D surface, but they differ in realism and measurement. An oblique sketch is often easier to draw but may appear distorted as it does not maintain accurate proportions. An isometric sketch, typically drawn on isometric dot paper, preserves the proportional lengths of the edges, resulting in a more realistic depiction of the solid shape.
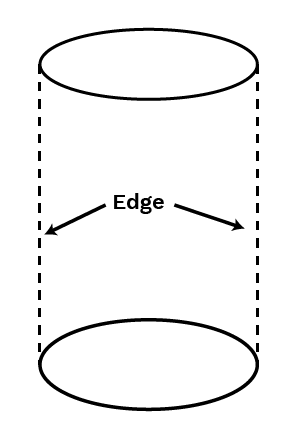
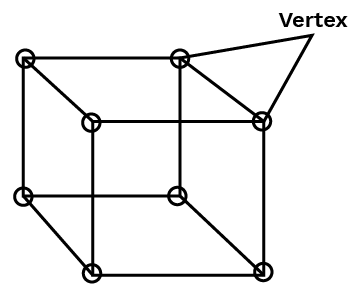
4. How are faces, vertices, and edges related in a polyhedron?
The relationship between faces, vertices, and edges in any convex polyhedron is defined by Euler's formula. This essential formula states that the number of Faces (F) plus the number of Vertices (V), minus the number of Edges (E), always equals 2. The formula is expressed as: F + V - E = 2. This is a crucial concept to remember for verifying the properties of solid shapes.
5. Why are revision notes helpful for understanding concepts like nets and different views of solids?
Revision notes are particularly effective for a visual chapter like this because they condense complex spatial ideas into simple, memorable points. For nets, notes can illustrate common examples and rules for identifying them. For different views (top, front, side), notes can provide clear diagrams that connect the 3D object to its 2D representations, making it easier to grasp the concept of perspective without needing physical models each time.
6. What is an effective strategy to revise a visual chapter like 'Visualising Solid Shapes'?
For a visual chapter, revision should be an active process. Begin by summarising the definitions of key terms like faces, nets, and isometric sketches. Then, actively practice by drawing a few simple oblique and isometric sketches of a cube or a cuboid. Finally, challenge yourself by observing an everyday object, like a duster or a water bottle, and attempting to sketch its top, front, and side views. This hands-on approach significantly strengthens visual comprehension.
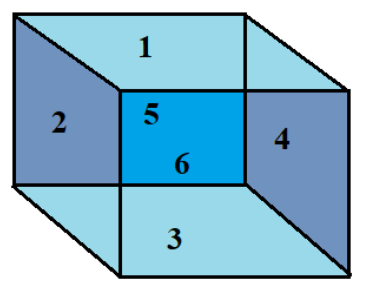
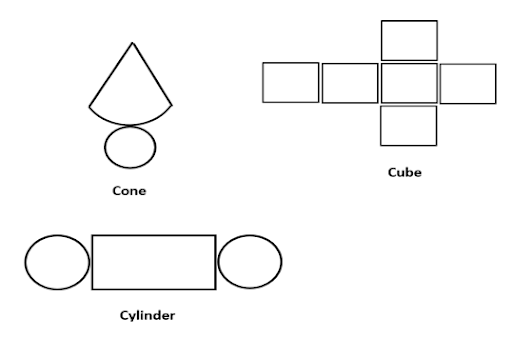
7. Can any 2D arrangement of six squares be folded into a cube? How can you quickly check if a net is valid?
No, not every arrangement of six squares can form a cube. A quick method to check a potential net is to visualise the folding process. A valid net for a cube must allow all faces to enclose a space without any overlap. A helpful trick is to identify a base face and then mentally fold the other faces upwards to see if they form the sides and a top. For instance, six squares arranged in a single long row cannot form a cube.
8. How does slicing a solid shape help in understanding its internal structure?
Slicing a solid shape reveals its cross-section, which is the 2D shape of the surface exposed by the cut. This is a powerful technique for understanding the internal composition of a 3D object. For instance:
- Slicing a cylinder parallel to its base reveals a circle.
- Slicing a cylinder vertically through its centre reveals a rectangle.
- Slicing a cube horizontally or vertically reveals a square.
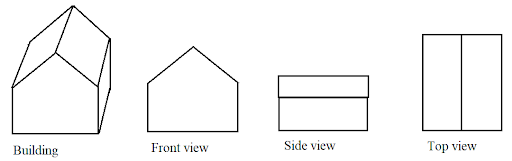
9. How do the top, front, and side views of an object relate to drawing its isometric sketch?
The different views of an object serve as the fundamental blueprint for creating an accurate isometric sketch. The front, top, and side views provide the correct dimensions and features for each respective face of the solid. When you draw an isometric sketch, you are effectively combining these three separate 2D views into a single, cohesive 3D representation that shows the object from a specific angle while preserving its proportions. Mastering the views first makes sketching the complete solid much more straightforward.
