Maths Notes for Chapter 1 Where to Look from Class 3 - FREE PDF Download
Introduction to Different Kinds of Views
Side View: When a person views an object from the side instead of front or back.
Front View: When an object is viewed from the front by an observer.
Back View: When an object is viewed from the back by an observer.
Top View: When an object is viewed from the top by an observer.
Bottom View: When an object is viewed from the bottom by an observer.
Solved Examples
1. Which of the following figures has the top view of a table?
Side and Top View of The table
Ans. From the above two figures, the First figure shows a side view of a table, when we will observe the table from the top, the top view of the table will be the below-given figure
(Image will be uploaded soon)
2. Draw the side, front and top view of the following given figure?
Views of Squares Blocks
Ans. The side, front and top views of the above figure are given below :
Side, Front and Top View of Square Blocks
In the side view of a figure, we will observe two square blocks.
In the front view of a figure, we will observe three square blocks.
In the top view of a figure, we will observe two square blocks.
3. Draw the front, side and top view of the given figure?
Different View of The Hut
Ans. The top, front and side views are shown below :
Front View, Side View and Top View of a Hut
Rangoli Patterns
We use Rangoli Patterns in Maths to find symmetry and reflection.
It can be done by joining the dotted lines on the dot grid to find symmetry and the reflection of different figures.
In mathematics, the rangoli symbols go on expanding to form a line and the basic geometrical shapes like the circle, triangle, square, rectangle and so on
Solved Example
1. A dot grid is given below, you are required to draw a kite, leaf, flower, boat, star and a pot on it?
Dot Grid
Ans: The required figures on the dot grid are drawn given below :
Shape Formation by Dot Grid
We can observe a kite, leaf, flower, boat, star and pot in the above figure.
Mirror Halves
Mirror ( or reflection ) symmetry divides a figure or design into halves that are mirror images.
In other words, objects are the same on both sides of a line ( usually in the middle).
Example of Mirror Halves are wings of Butterfly can be exactly get halved and Letter words like H, Y W X are the examples of Mirror halves as they can be exactly cut into two halves
Solved Example
1. Draw the Mirror halves of the following figures?
Mirror Halves
Ans.
Figure(a) clearly shows the Mirror half of the capital letter A, and we have to draw the other mirror half of it. The required other mirror half is given below
Mirror Image of Half A
Figure(b) clearly shows the Mirror half of the capital letter D, and we have to draw the other mirror half of it. The required other mirror half is given below
Mirror Image of Half D
Figure(c) clearly shows the Mirror half of the capital letter N, and we have to draw the other mirror half of it. The required other mirror half is given below
Mirror Image of Half N
Figure(d) clearly shows the Mirror half of the capital letter H, and we have to draw the other mirror half of it. The required other mirror half is given below
Mirror Image of Half H
Reflection Symmetry
When the first half of an object reflects the other half of the object in the mirror, then we call it Reflection Symmetry.
Reflection Symmetry can also be named Mirror Symmetry.
For example, in general, human faces are identical on the left and right sides. The wings of most butterflies are identical on both sides, the left and right sides.
Finding Reflection Symmetry
The first half of an object must be a reflection of the other half of an object.
Imagine folding a rectangle along each line of symmetry and each of the half matching up perfectly, this is symmetry
For the two symmetrical halves, one of them follows lateral inversion, that is the left side appears to be the right side as it happens when you look in a mirror.
For Example The reflection of trees in clear water, and the reflection of mountains in a lake are among the commonly seen examples of reflection symmetry around us.
Practise Problems
Q1. Draw some figures out of your imagination which can be exactly cut into two halves?
Q2. Below are some given pictures, and you have to think from what kind of view these pictures will seem like this?
Different Kinds of Views
Ans: Below is some required figures that can be exactly cut into two halves
Equal Halves
Ans:
Staircase - Side View is seen
Staircase - Top View is seen
Table - Top View is seen
Chair - Side View is seen
Pencil - Top View is seen
Bus - Side View is seen
Importance of Where to Look From Class 3 Maths Worksheets
This chapter has been formulated with the prime aim of instilling skills to recognize the different sections of images and objects. It helps the students of Class 3 to identify the mirror halves of alphabets and images. They will also gain an understanding of what images look like in a reflection, with the help of the Where to Look From Class 3 Maths worksheets.
This chapter is important in terms of creating a better understanding of geometrical figures. These revision notes will encourage students of Class 3 to think of the actual representation of images and objects we see every day.
This perception of shapes and level of visibility of objects from 2D images will develop new skills related to 2D and 3D geometry. Class 3 students will understand what part of the objects will be visible if looked at from a particular angle.
Proceeding to the next level of this chapter, students will learn what the mirror halves of objects and images look like. They will get to learn what lateral inversion is by studying the mirror halves of images, alphabets, and objects. Studying a mirror half image will develop exceptional skills to identify, draw, and comprehend shapes for higher classes.
Benefits of Where to Look From Class 3 Maths Worksheets
Apart from the exercise questions, the young inquisitive minds will need something to quench their zeal. So we have provided well-organized worksheets for their practice. They can download the Where to Look From Class 3 Maths PDF to get the worksheets of this chapter, prepared by our subject matter experts.
The questions in the worksheets are framed with the prime objective to check the level of understanding of the concepts among students. These worksheet questions will also have answers. After having finished studying Where to Look From, students can focus on solving the worksheets.
Solving a worksheet will help them evaluate their skills to perceive geometrical images and their specific angles. Students will also be able to comprehend 2D and 3D geometry easily in higher classes.
So enjoy studying the concise and accurate Where to Look From revision notes and use them as references when you are preparing for the exams. You can also refer to the other relevant study materials for this chapter on Vedantu.
Important Related Links for CBSE Class 3
Study Materials for CBSE Class 3 Maths
FAQs on Where to Look from Class 3 Maths Chapter 1 CBSE Notes - 2025-26
1. What key concepts are covered in the Class 3 Maths revision notes for Chapter 1, 'Where to Look From'?
The revision notes for 'Where to Look From' provide a quick summary of essential concepts for the 2025-26 syllabus. Key topics include understanding how objects appear from different viewpoints like the top view, side view, and front view, the idea of symmetry through mirror halves, and the creation of patterns like Rangoli.
2. How do the revision notes explain the concept of 'mirror halves'?
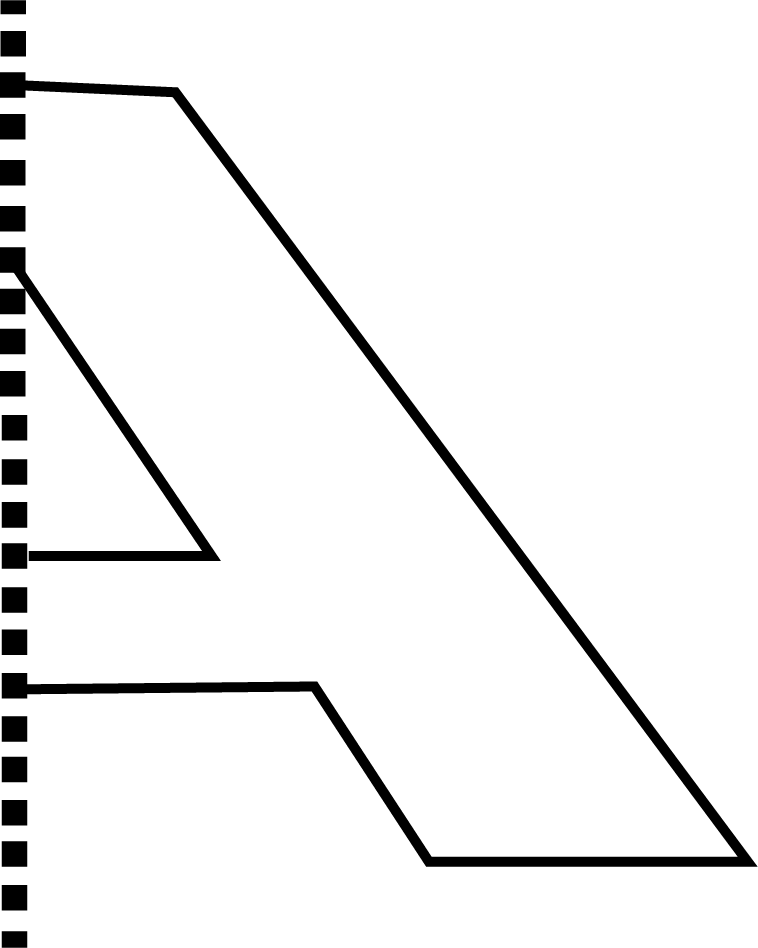
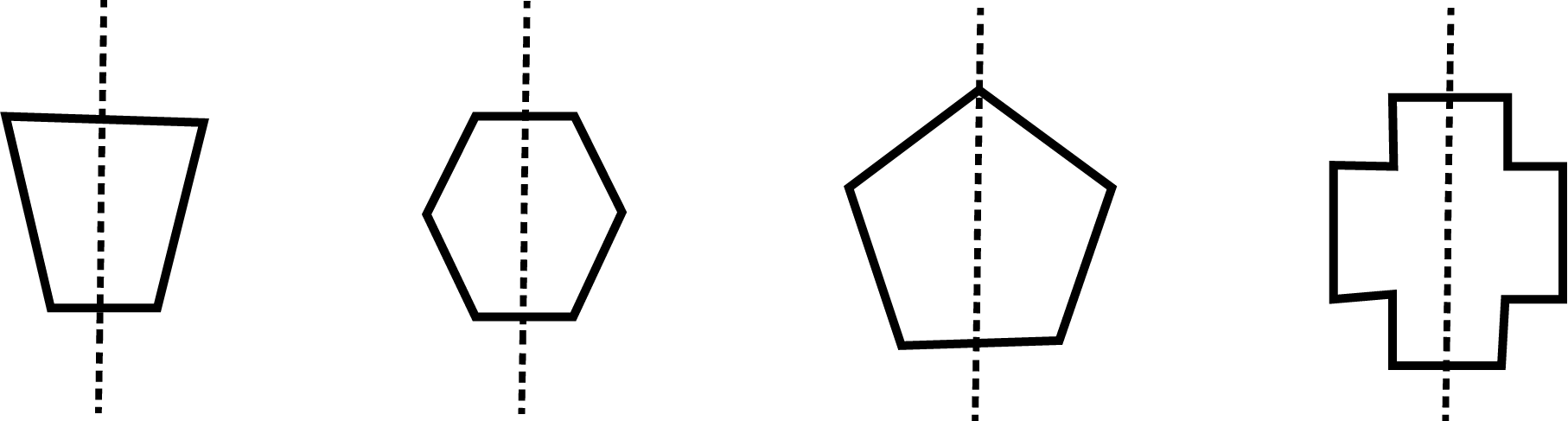
The notes explain that a 'mirror half' refers to one side of a symmetrical object. If you draw a dotted line (line of symmetry) down the middle of an object like the letter 'A' or a butterfly, both sides are identical. The notes clarify that if you were to place a mirror on this line, the reflection would complete the shape perfectly, hence the name mirror half.
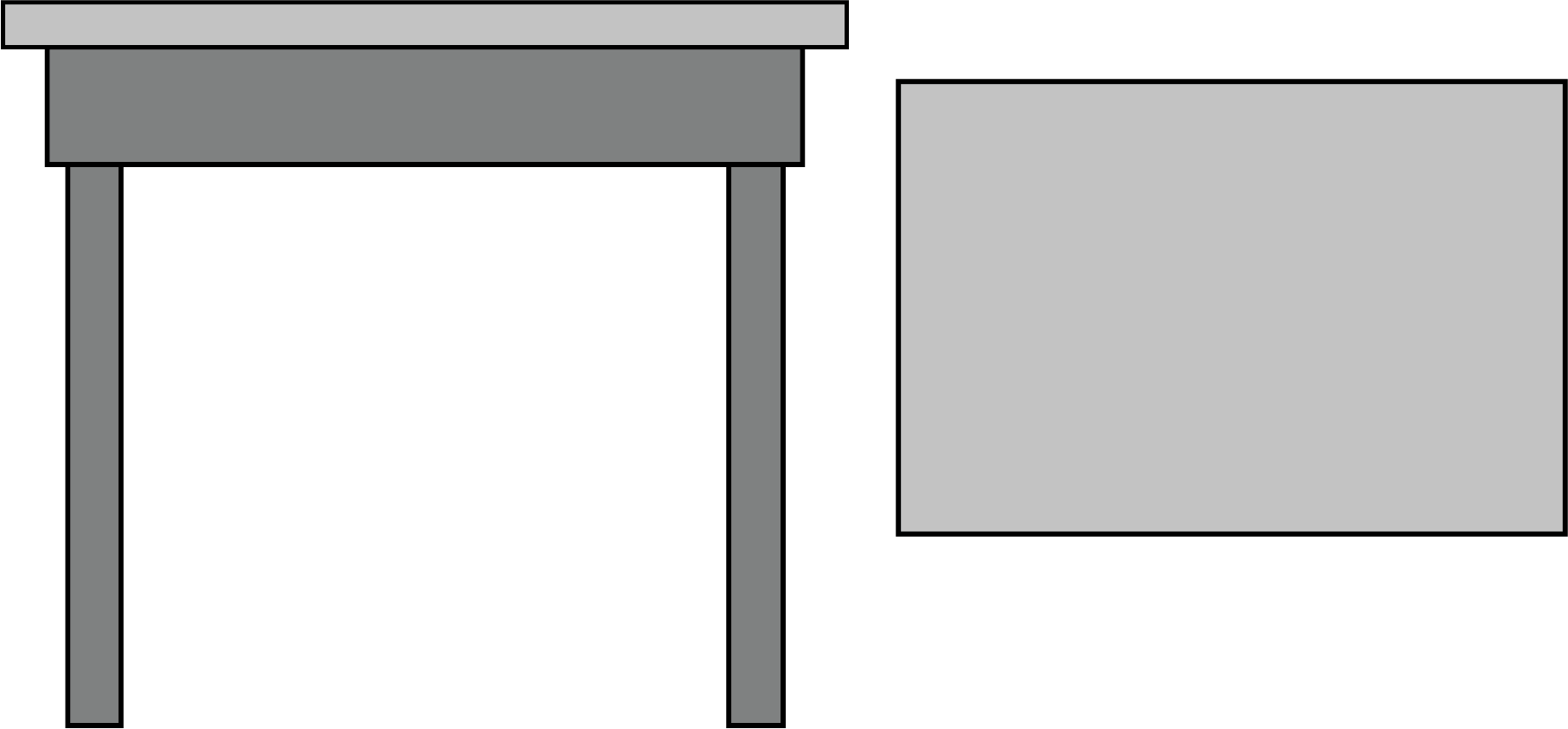
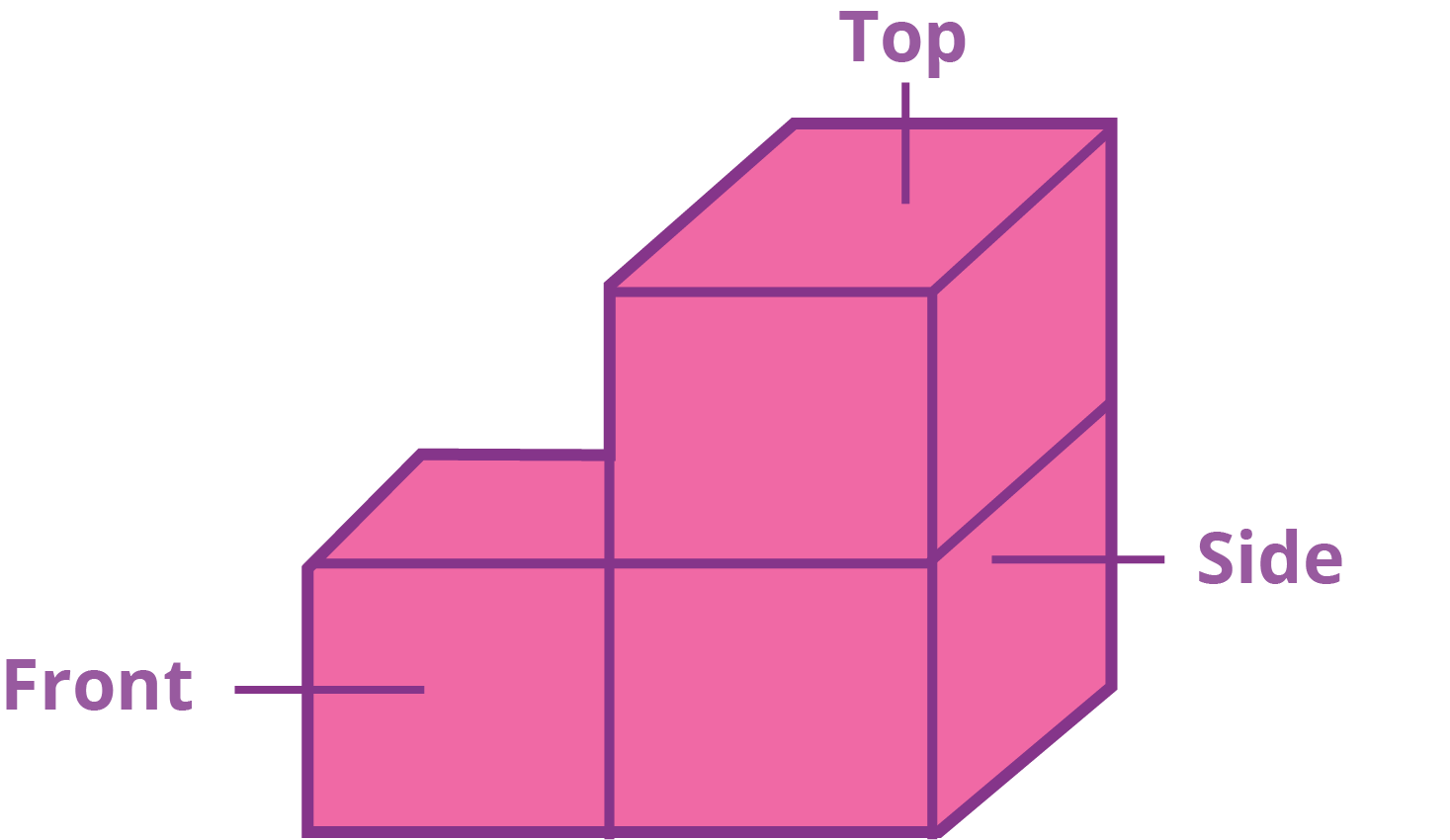
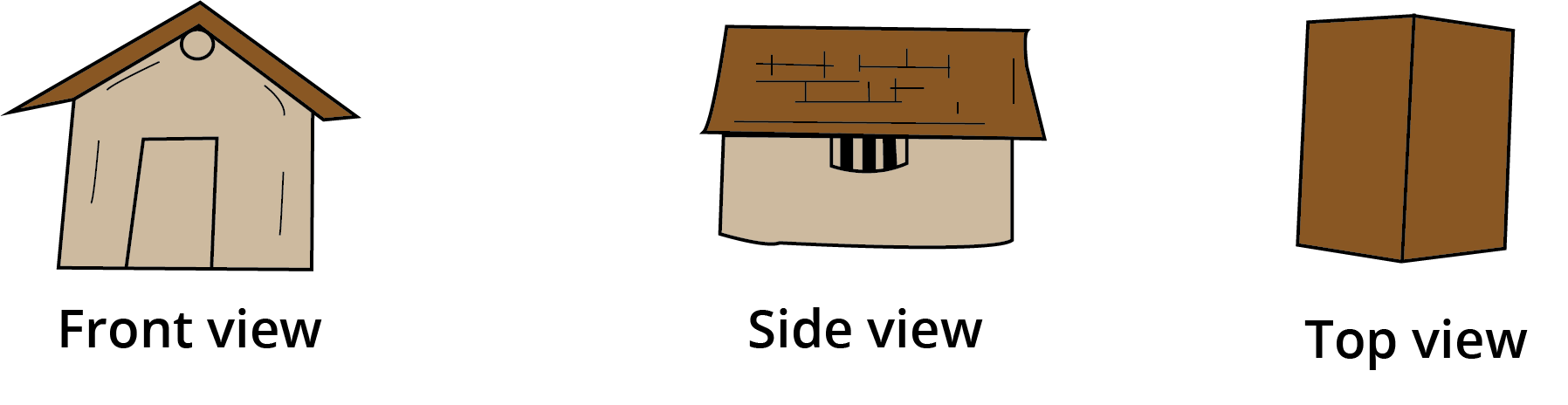
3. Why is it important for a Class 3 student to learn about different views of an object?
Learning about different views is crucial as it builds a child's spatial reasoning and visualisation skills. This foundational concept from the NCERT syllabus helps students understand how 2D drawings can represent 3D objects, a skill that is important not just in Maths and drawing, but also in understanding maps and real-world structures.
4. How can the concept of symmetry from these revision notes be applied in real life?
The concept of symmetry is everywhere, and these notes help you recognise it. You can apply this by:
Noticing the symmetry in nature, like in leaves, flowers, and insects.
Creating symmetrical art and craft, such as folding a paper and cutting a shape to make a symmetrical design.
Observing symmetry in architecture and objects around your home, like windows, plates, and furniture.
5. What is the main purpose of studying Rangoli patterns in this chapter?
Studying Rangoli patterns helps students see a fun and practical application of symmetry and patterns. The revision notes summarise how these complex-looking designs are often made from simple, repeating symmetrical shapes on a dot grid. It reinforces the idea that Maths concepts can be used to create beautiful art.
6. How do the revision notes help distinguish between an object's top view and front view?
The notes use simple examples to clarify the difference. The top view is what you see when you look down at an object from directly above, like seeing the circular lid of a bottle. The front view is what you see looking at it from the front, like seeing the label on the same bottle. The notes use clear diagrams to make this distinction easy to revise.
