Maths Notes for Chapter 9 Some Applications of Trigonometry Class 10 - FREE PDF Download
Some Applications of Trigonometry Class 10 Maths Chapter 9 CBSE Notes - 2025-26



FAQs on Some Applications of Trigonometry Class 10 Maths Chapter 9 CBSE Notes - 2025-26
1. What are the key concepts covered in the revision notes for Some Applications of Trigonometry Class 10?
Some Applications of Trigonometry Class 10 revision notes focus on core concepts such as:
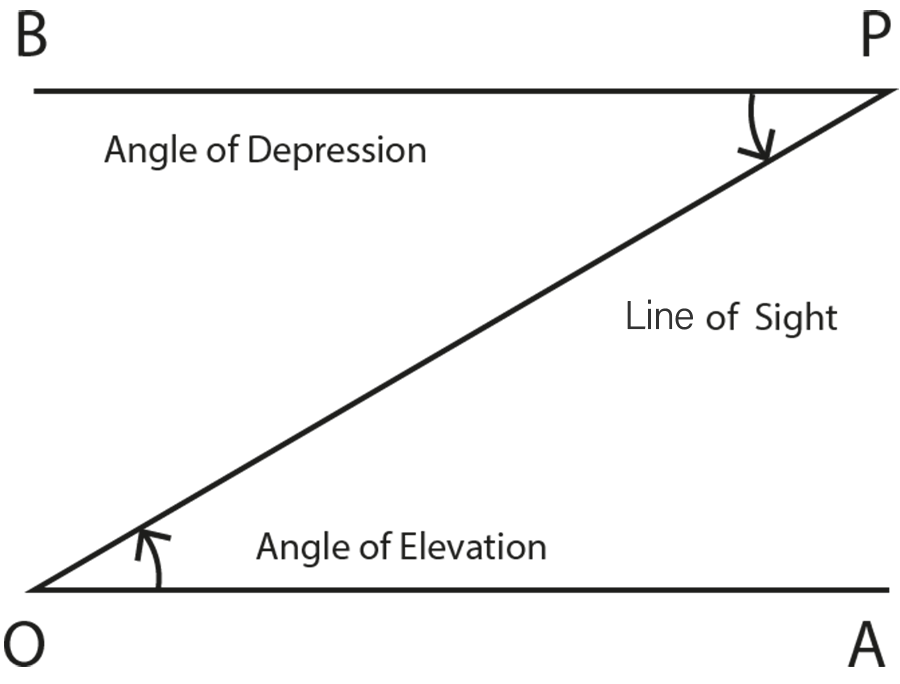
- Line of sight, angle of elevation, and angle of depression
- Using trigonometric ratios for calculating heights and distances
- Problem-solving strategies for real-life applications
- Application of tan, sin, and cos in statement-based questions
2. How should I revise Some Applications of Trigonometry Class 10 for board exams?
To effectively revise Some Applications of Trigonometry Class 10, follow these steps:
- Review all key formulas and definitions such as angle of elevation and depression
- Practice solving at least 4–5 previous year problems daily
- Refer to concise revision notes before attempting statement-based questions
- Focus on drawing accurate diagrams for each type of application question
3. What are the essential formulas included in the Class 10 Maths Chapter 9 revision notes?
The essential formulas in Class 10 Maths Chapter 9 include:
- tan θ = Opposite/Adjacent
- sin θ = Opposite/Hypotenuse
- cos θ = Adjacent/Hypotenuse
- Heights and distances problems using trigonometric ratios
4. How are angles of elevation and depression used in real-life problems as per Class 10 revision notes?
Angles of elevation and depression are practical tools to find unknown heights or distances in real life. According to the revision notes:
- Angle of elevation helps calculate the height of a tall object when observed from the ground
- Angle of depression is used when the observer looks downward from a height
- Both require the use of right triangles and trigonometric ratios to solve
5. What is the typical order of revision recommended for Some Applications of Trigonometry Class 10?
The optimal order of revision is:
- Begin with definitions: line of sight, angles of elevation and depression
- Cover trigonometric ratios and their values
- Move to formula application in simple height/distance problems
- Advance to mixed and multi-step statement-based questions
- Finish by revisiting key points and practicing previous year questions
6. Why is Chapter 9 Some Applications of Trigonometry considered a scoring chapter in Class 10 Maths?
Chapter 9 is scoring because:
- It features standard types of problems, making preparation straightforward
- Most questions can be solved via formulaic approaches and diagram work
- Regular practice improves both speed and accuracy
- The chapter carries significant weightage (12 marks) in CBSE Board exams
7. How do I avoid common mistakes when solving Class 10 trigonometry application problems?
To avoid common mistakes:
- Always identify and label right angles correctly in diagrams
- Assign known and unknown values before calculations
- Double-check the formula (sin/cos/tan) suitable for each triangle
- Mind the angle: elevation for upward sight, depression for downward
- Review units and ensure logical dimensions (e.g., m, km)
8. What is a 'statement-based question' in the context of Some Applications of Trigonometry, and how should I approach it?
A statement-based question describes a real-world scenario (like a tower or kite) and asks for calculation of height, distance, or length. To approach:
- Carefully read and identify all quantitative data
- Draw a labelled diagram as per the scenario
- Select the right trigonometric ratio
- Formulate the equation and solve step by step
9. What are some frequently misunderstood areas in Class 10 Applications of Trigonometry that I should watch out for?
Frequently misunderstood areas include:
- The difference between angle of elevation (observer looks up) and depression (observer looks down)
- Misinterpreting the positioning of observer and object in diagrams
- Mixing up when to use sin, cos, or tan for a specific triangle
- Overlooking conversion of units or incorrect labelling
10. How can revision notes help with last-minute preparation for Class 10 Board Maths exams?
Revision notes enable last-minute preparation by:
- Presenting all formulas, definitions, and key examples in a summarized format
- Allowing rapid review of important points without reading the entire textbook
- Boosting confidence through targeted practice right before the exam
- Supporting a focused approach to commonly tested question types
11. What is the 'line of sight' in the context of Class 10 Maths Chapter 9?
The line of sight is the imaginary straight line drawn from the observer’s eye to the object being observed. It forms the basis for calculating angles of elevation and depression in application problems, as per the Class 10 CBSE 2025–26 syllabus.
12. Can you list the key terms every student must remember from Class 10 Some Applications of Trigonometry?
The key terms to remember are:
- Angle of Elevation
- Angle of Depression
- Line of Sight
- Trigonometric Ratios (sin, cos, tan)
- Height and Distance
- Hypotenuse, Opposite, Adjacent sides
13. How do angles of elevation and depression relate to the properties of triangles used in Chapter 9?
Both angles of elevation and depression are always associated with right-angled triangles formed in the scenario. The observer, the object, and the horizontal plane together create a triangle, allowing the use of trigonometric ratios to solve for unknown heights or distances. Application of this triangle property is essential for CBSE board exam problems.
14. In what ways can regular revision notes practice help improve problem-solving speed for Class 10 applicants?
Regular practice with revision notes helps by:
- Familiarizing the student with repeated question formats
- Ensuring quick recall of formulas and calculation steps
- Building confidence through exposure to diverse solved examples
- Developing a habit of drawing and interpreting diagrams efficiently
15. What special advice is given for revision before attempting statement-based questions in Class 10 Maths Chapter 9?
Before attempting statement-based questions in Chapter 9:
- Revise all definitions and standard formulas
- Skim through solved examples to recall the logical approach
- Ensure a clear understanding of diagram construction
- Double-check units and angle specifications




















 Watch Video
Watch Video