
\[y\] component of velocity is \[20\;\]and \[x\;\] a component of velocity is \[10\]. The direction of motion of the body with the horizontal at this instant is
A. \[{\tan ^{ - 1}}(2)\]
B. \[{\tan ^{ - 1}}(1/2)\]
C. \[{45^0}\]
D. \[{0^0}\]
Answer
391.5k+ views
Hint: The motion of two-dimensional motion is more complex than one-dimensional motion. This is because velocities can move in diagonal directions. This means that the object is moving both vertically and horizontally at the same time. We break up this velocity vector into two components: the vertical velocity component and the horizontal velocity component to simplify our calculations.
Complete step by step solution:
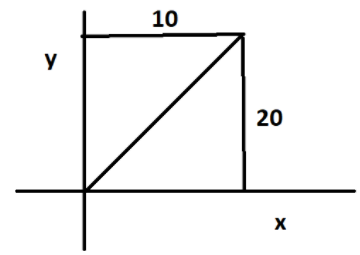
Given that the horizontal velocity component \[{v_x}\]=\[10\]
Vertical velocity component \[{v_y}\]=\[20\]
Therefore from the trigonometric formula, we know that,
\[\tan \theta = \dfrac{{{\text{Opposite}}}}{{Adjacent}}\]
From the diagram above we can form a triangle and substitute the velocity component values in the formula. Therefore we get,
\[\tan \theta = \dfrac{{20}}{{10}}\]
\[\tan \theta = 2\]
\[\theta = {\tan ^{ - 1}}2\]
Therefore the correct option is A.
Additional Information:
Breaking up the velocity acting in the diagonal direction into its vertical and horizontal components helps us to deal with each direction separately. This helps to convert a difficult two-dimensional problem into two separate one-dimensional problems. Like we break velocity into two components we can also break other vectors like electric fields, momentum, and forces.
To find the magnitude of the velocity vector we can use the Pythagoras theorem. Since every right angle triangle uses this theorem to find the sides of the triangle.
\[{v^2} = {v_x}^2 + {v_y}^2\]
\[v = \sqrt {{v_x}^2 + {v_y}^2} \]
Note:
In the above-solved problem, we have put the \[{v_y}\] component on the numerator and the \[{v_x}\] component on the denominator. This is because we have considered \[{v_y}\] as the opposite side and \[{v_x}\] as the adjacent side. This means that we are measuring this angle from the horizontal axis. To figure out how to find the angle there are two tips. We have to select right/up as positive directions. If\[{v_x}\]is positive then the vector points rightward but if \[{v_x}\] is negative the vector points are leftwards. On the other hand, if \[{v_y}\] is positive then the vector points upwards and if \[{v_y}\] is negative then the vector points downward.
Complete step by step solution:

Given that the horizontal velocity component \[{v_x}\]=\[10\]
Vertical velocity component \[{v_y}\]=\[20\]
Therefore from the trigonometric formula, we know that,
\[\tan \theta = \dfrac{{{\text{Opposite}}}}{{Adjacent}}\]
From the diagram above we can form a triangle and substitute the velocity component values in the formula. Therefore we get,
\[\tan \theta = \dfrac{{20}}{{10}}\]
\[\tan \theta = 2\]
\[\theta = {\tan ^{ - 1}}2\]
Therefore the correct option is A.
Additional Information:
Breaking up the velocity acting in the diagonal direction into its vertical and horizontal components helps us to deal with each direction separately. This helps to convert a difficult two-dimensional problem into two separate one-dimensional problems. Like we break velocity into two components we can also break other vectors like electric fields, momentum, and forces.
To find the magnitude of the velocity vector we can use the Pythagoras theorem. Since every right angle triangle uses this theorem to find the sides of the triangle.
\[{v^2} = {v_x}^2 + {v_y}^2\]
\[v = \sqrt {{v_x}^2 + {v_y}^2} \]
Note:
In the above-solved problem, we have put the \[{v_y}\] component on the numerator and the \[{v_x}\] component on the denominator. This is because we have considered \[{v_y}\] as the opposite side and \[{v_x}\] as the adjacent side. This means that we are measuring this angle from the horizontal axis. To figure out how to find the angle there are two tips. We have to select right/up as positive directions. If\[{v_x}\]is positive then the vector points rightward but if \[{v_x}\] is negative the vector points are leftwards. On the other hand, if \[{v_y}\] is positive then the vector points upwards and if \[{v_y}\] is negative then the vector points downward.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

The correct geometry and hybridization for XeF4 are class 11 chemistry CBSE

Water softening by Clarks process uses ACalcium bicarbonate class 11 chemistry CBSE

With reference to graphite and diamond which of the class 11 chemistry CBSE

Trending doubts
10 examples of friction in our daily life

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

State and prove Bernoullis theorem class 11 physics CBSE

State the laws of reflection of light

Write down 5 differences between Ntype and Ptype s class 11 physics CBSE




