Question

What is the value of linear velocity? If \[\vec \omega = 3\hat i + 4\hat j + \hat k\] and \[\vec r = 5\hat i - 6\hat j + 6\hat k\]

Answer 1

Hint: When a body moves in the angular way i.e. circular motion and rotatory motion, with constant speed, it’s direction changes continuously so the angular velocity of body changes with respect to time, hence it has a linear velocity which is we are going to find. By remembering that it is a velocity not the speed because in uniform circular/rotational motion the speed remains constant. The linear and angular velocities both are vector quantities.

Formula used: Relation between linear velocity and angular velocity-
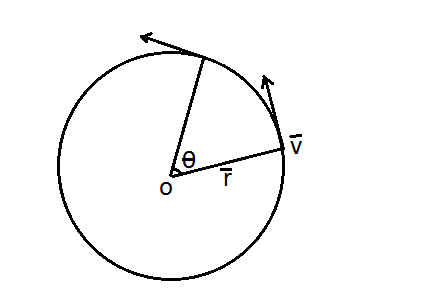
  \[\vec v = \vec r \times \vec \omega \]
Where \[\vec v\] is linear velocity of body, \[\vec \omega \] is angular velocity of body, \[\vec r\] is the radius of Path.

Complete step by step solution:
The linear velocity of any rotating body is defined as the cross product of the angular velocity and the radius of path. In this question the angular velocity and the radius of path, in which the body is moving is given as –
\[\vec \omega = 3\hat i + 4\hat j + \hat k\]
\[\vec r = 5\hat i - 6\hat j + 6\hat k\]
\[\vec v = ?\]
        

We know from the relation of linear velocity and angular velocity
\[\vec v = \vec r \times \vec \omega \]
\[
   \Rightarrow \vec v = (5\hat i - 6\hat j + 6\hat k) \times (3\hat i + 4\hat j + \hat k) \\
   \Rightarrow \vec v = \left| {\begin{array}{*{20}{c}}
  {\hat i}&{\hat j}&{\hat k} \\
  5&{ - 6}&6 \\
  3&4&1
\end{array}} \right| \\
   \Rightarrow \vec v = \hat i\{ - 6 - 24\} - \hat j\{ 5 - 18\} + \hat k\{ 20 - ( - 18)\} \\
   \Rightarrow \vec v = \hat i( - 6 - 24) - \hat j(5 - 18) + \hat k(20 + 18) \\
   \Rightarrow \vec v = \hat i( - 30) - ( - 13)\hat j + 38\hat k \\
   \Rightarrow \vec v = 30\hat i + 13\hat j + 38\hat k \\
\]
Hence, the linear velocity of the body is \[\vec v = 30\hat i + 13\hat j + 38\hat k\]

Additional Information: The magnitude of linear velocity is \[m/{s^2}\]and for a complete revolution the average velocity of any rotating body is always zero. And angular acceleration is also found by this velocity.
Angular velocity = the rate of change of angular displacement with respect to time is called angular velocity. And denoted by\[\vec \omega \].
Angular acceleration = the rate of change of angular velocity with respect to time is called angular acceleration. And denoted by\[\vec a\].
 \[
  \vec a = \dfrac{{{{\vec v}^2}}}{r} \\
   \Rightarrow \vec a = \dfrac{{{r^2}{\omega ^2}}}{r} \\
   \Rightarrow \vec a = r{\omega ^2} \\
\]
Angular acceleration is always changing with the change of direction.

Note:When we find the cross product of \[r\]and\[\omega \], \[\hat j\] is taken as negative. If angle is given in the problem than we can apply the formula \[\vec A \times \vec B = \left| A \right|\left| B \right|\sin \theta \]
Where \[\left| A \right|\]is magnitude of\[\vec A\] and \[\left| B \right|\] is the magnitude of\[\vec B\].