Question

Use Huygens principle to explain the formation of diffraction patterns due to a single shit illuminated by a monochromatic source at light. When the width of the shit is made double the original width, how would this affect the size and intensity of the central diffraction band?

Answer 1

Hint: Use the concept of Huygens’s principle.
Use the young slit experiment for this problem.

Complete step by step solution:
According to the Huygen's principle "The net effect at any point due to the number of wavelets is equals to sum total contribution at all wavelets with proper phase difference

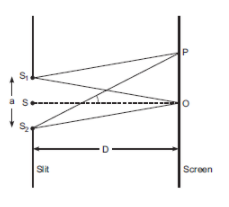
The point N is Maxima because from each part of the slit S₁ RS₂ is in phase means the path difference is O.
At point M
(i) If \[{{S}_{2}}i-{{S}_{1}}i=n\lambda \] then point p would be minimum
(ii) If \[{{S}_{2}}P-{{S}_{1}}P=\left( 2n+1 \right)\dfrac{\lambda }{2}\] then point P would be Maxima. At the point of Maxima, intensity will decrease.
The width of the central Maxima is given by \[\dfrac{S\lambda D}{a}\]
Where
\[\lambda =\]Wavelength
\[D=\] Distance between screen and the slit
\[a=\] Size of the slit
When the width of the slit is made double the original width then the size of the central maxima will be reduced to half and intensity will be four times.

Note: Student should be better understanding of Huygens’s principle. The young slit experiment observes carefully. The width of the slit makes a huge impact on calculations.