
Two mirrors, one concave and the other convex, are placed 60 cm apart from with their reflecting surfaces facing each other. An object is placed 30 cm from the pole of either of them on their axis. If the focal lengths of both the mirrors are 15 cm, what will be the position of the image formed by reflection, first at the convex mirror and then at the concave mirror?
A. 19.09 cm from the pole of the concave mirror.
B. 19.09 cm from the pole of the convex mirror.
C. 11.09 cm from the pole of the concave mirror.
D. 11.09 cm from the pole of the convex mirror.
Answer
188.7k+ views
Hint: First the light from the object will be reflected at the convex mirror and it will create its image. Now, this image will act as a virtual object for the concave mirror, at which the reflection takes place and then the second image will be formed. Keeping in mind the sign convention, solve for the image distance for each mirror, using the Mirror Formula.
Formula used:
Mirror Formula:
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$ … (1)
Here, $f$ is the focal length of the mirror,
$u$ is the object distance and
$v$ is the image distance.
Complete answer:
By Mirror Formula we know that:
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$ … (1)
Let the convex mirror at which the first reflection occurs be ${M_1}$ and let the concave mirror at which the second reflection occurs be ${M_2}$ .
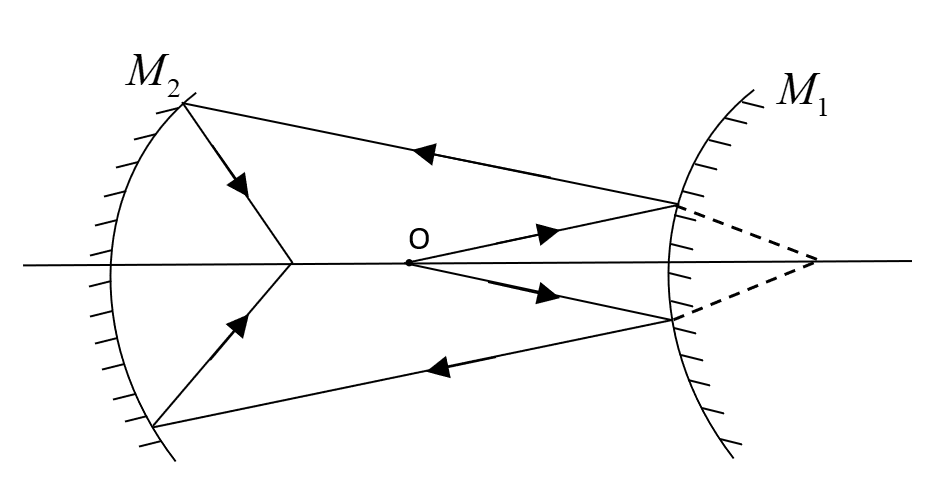
It is given that the focal length of the two mirrors is 15 cm respectively and they are separated by a distance of 60 cm.
It is also given that the object is placed 30 cm from the pole of either of the two mirrors.
Now, let us first consider the reflection taking place at the convex mirror ${M_1}$ .
Focal length of a convex mirror is positive, therefore, $f = 15{\text{ cm}}$
Object distance, $u = - 30{\text{ cm}}$
Now applying Mirror Formula as given in equation (1),
$\dfrac{1}{v} = \dfrac{1}{{15}} + \dfrac{1}{{30}} = \dfrac{1}{{10}}$
This gives $v = 10{\text{ cm}}$ .
Thus, the first image is formed behind the convex mirror at a distance of 10 cm from its pole.
Now, this image will act as the object for the concave mirror.
Let us now consider the reflection taking place at the concave mirror ${M_2}$ .
Focal length of a concave mirror is negative, therefore, $f = - 15{\text{ cm}}$
Object distance, $u = - (60 + 10) = - 70{\text{ cm}}$
Now applying Mirror Formula as given in equation (1),
$\dfrac{1}{v} = - \dfrac{1}{{15}} + \dfrac{1}{{70}} = \dfrac{{ - 14 + 3}}{{210}} = \dfrac{{ - 11}}{{210}}$
Thus, $v = \dfrac{{ - 210}}{{11}} = - 19.09{\text{ cm}}$ .
Hence, the second image is formed in front of the concave mirror at a distance of 19.09 cm from its pole.
This is the required image distance.
Thus, the correct option is A.
Note: Sign convention is very important in Ray Optics. The directions are measured from the poles of the mirror. The direction of the incident ray is considered to be positive, and any distance measured along the incident ray is positive, else every distance is negative. Therefore, in the above question, for each mirror, we have considered its own sign convention.
Formula used:
Mirror Formula:
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$ … (1)
Here, $f$ is the focal length of the mirror,
$u$ is the object distance and
$v$ is the image distance.
Complete answer:
By Mirror Formula we know that:
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$ … (1)
Let the convex mirror at which the first reflection occurs be ${M_1}$ and let the concave mirror at which the second reflection occurs be ${M_2}$ .

It is given that the focal length of the two mirrors is 15 cm respectively and they are separated by a distance of 60 cm.
It is also given that the object is placed 30 cm from the pole of either of the two mirrors.
Now, let us first consider the reflection taking place at the convex mirror ${M_1}$ .
Focal length of a convex mirror is positive, therefore, $f = 15{\text{ cm}}$
Object distance, $u = - 30{\text{ cm}}$
Now applying Mirror Formula as given in equation (1),
$\dfrac{1}{v} = \dfrac{1}{{15}} + \dfrac{1}{{30}} = \dfrac{1}{{10}}$
This gives $v = 10{\text{ cm}}$ .
Thus, the first image is formed behind the convex mirror at a distance of 10 cm from its pole.
Now, this image will act as the object for the concave mirror.
Let us now consider the reflection taking place at the concave mirror ${M_2}$ .
Focal length of a concave mirror is negative, therefore, $f = - 15{\text{ cm}}$
Object distance, $u = - (60 + 10) = - 70{\text{ cm}}$
Now applying Mirror Formula as given in equation (1),
$\dfrac{1}{v} = - \dfrac{1}{{15}} + \dfrac{1}{{70}} = \dfrac{{ - 14 + 3}}{{210}} = \dfrac{{ - 11}}{{210}}$
Thus, $v = \dfrac{{ - 210}}{{11}} = - 19.09{\text{ cm}}$ .
Hence, the second image is formed in front of the concave mirror at a distance of 19.09 cm from its pole.
This is the required image distance.
Thus, the correct option is A.
Note: Sign convention is very important in Ray Optics. The directions are measured from the poles of the mirror. The direction of the incident ray is considered to be positive, and any distance measured along the incident ray is positive, else every distance is negative. Therefore, in the above question, for each mirror, we have considered its own sign convention.
Recently Updated Pages
Uniform Acceleration: Definition, Equations & Graphs for JEE/NEET

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

JEE Electricity and Magnetism Important Concepts and Tips for Exam Preparation

Electrical Resistance - Important Concepts and Tips for JEE

Trending doubts
Atomic Structure: Definition, Models, and Examples

Centre of Mass of Hollow and Solid Hemisphere Explained

Average and RMS Value in Physics: Formula, Comparison & Application

Centre of Mass of a Semicircular Ring: Concept, Derivation & Uses

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main

Chemistry Question Papers for JEE Main, NEET & Boards (PDFs)




