
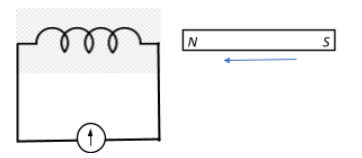
The variation of induced emf ($\epsilon$) with time (t) in a coil if a short bar magnet is moved along its axis with a constant velocity is best represented as:






Answer
527.7k+ views
Hint: From Faraday’s first law of electromagnetic induction we know that an emf is induced in the coil when the coil is exposed to a changing flux. One of the ways to vary the flux is to move the magnet in and out the coil. When this is done an emf is induced. Now, what is of importance to us is the direction in which the current flows through the loop of the coil as the magnet enters and leaves the coil. This is described by Lenz's law which suggests that the induced current assumes a polarity that will oppose the pole of the magnet near to it. To this end, determine which of the graphs represent a change in polarity.
Complete answer:
We can deduce the nature of the variation of emf with time by looking at the situation in the context of Faraday's first law of electromagnetic induction, and Lenz’s Law.
Faraday’s first law suggests that whenever the magnetic flux linked with a coil changes, an emf is induced in the coil. The induced emf exists as long as the change in magnetic flux continues to exist. Recall that magnetic flux here is nothing but the magnetic field lines emanating from the magnet.
Thus, when we move the bar magnet along the axis of the coil, the coil is being exposed to a varying magnetic field. This produces an emf in the coil.
Now, let us look at what happens as the magnet traverses into and out of the coil. This is best described by Lenz’s Law which states that the polarity (direction) of the induced emf is always such that it tends to produce a current which opposes the change in magnetic flux that initially produced it.
Let us say that the magnet is initially brought towards the coil with its north pole facing the loop. Now, as the magnet gets closer to the loop, the magnetic flux through the face of the coil increases. This induces an emf and consequently a current in the coil. Remember that the magnetic field lines of a magnet are directed from the N to the S pole inside the magnet. Using the right hand thumb rule, we see that the current induced in the coil flows in an anti-clockwise direction at the face of the coil. The face of the coil behaves like the N-pole.
Now, as the magnet passes through and comes out of the other end, the current is induced in a clockwise direction in this end of the coil, since the magnet’s field is still from N to S pole and the S pole is closest to this other face of the coil. This face of the coil behaves like the S-pole.
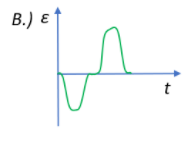
In both cases we see that there is a change in the polarity of the coil, and this change in polarity is clearly illustrated by only one graph.
Therefore, the correct option would be B.
Note:
Remember that the right hand “thumb” rule involves a closed fist, with the upright thumb pointing in the direction of current flow and the fist representing the direction of the magnetic field lines. We use this to determine the direction of flow of induced current.
Also, in addition to moving the magnet in and out of the coil, there are other ways to vary the magnetic field of the coil. This can be done by:
1. Moving the magnet towards the coil with a varying velocity.
2. Changing the plane of the coil through which the magnet moves.
3. Rotating a coil relative to the magnet.
Complete answer:
We can deduce the nature of the variation of emf with time by looking at the situation in the context of Faraday's first law of electromagnetic induction, and Lenz’s Law.
Faraday’s first law suggests that whenever the magnetic flux linked with a coil changes, an emf is induced in the coil. The induced emf exists as long as the change in magnetic flux continues to exist. Recall that magnetic flux here is nothing but the magnetic field lines emanating from the magnet.
Thus, when we move the bar magnet along the axis of the coil, the coil is being exposed to a varying magnetic field. This produces an emf in the coil.
Now, let us look at what happens as the magnet traverses into and out of the coil. This is best described by Lenz’s Law which states that the polarity (direction) of the induced emf is always such that it tends to produce a current which opposes the change in magnetic flux that initially produced it.
Let us say that the magnet is initially brought towards the coil with its north pole facing the loop. Now, as the magnet gets closer to the loop, the magnetic flux through the face of the coil increases. This induces an emf and consequently a current in the coil. Remember that the magnetic field lines of a magnet are directed from the N to the S pole inside the magnet. Using the right hand thumb rule, we see that the current induced in the coil flows in an anti-clockwise direction at the face of the coil. The face of the coil behaves like the N-pole.
Now, as the magnet passes through and comes out of the other end, the current is induced in a clockwise direction in this end of the coil, since the magnet’s field is still from N to S pole and the S pole is closest to this other face of the coil. This face of the coil behaves like the S-pole.
In both cases we see that there is a change in the polarity of the coil, and this change in polarity is clearly illustrated by only one graph.
Therefore, the correct option would be B.
Note:
Remember that the right hand “thumb” rule involves a closed fist, with the upright thumb pointing in the direction of current flow and the fist representing the direction of the magnetic field lines. We use this to determine the direction of flow of induced current.
Also, in addition to moving the magnet in and out of the coil, there are other ways to vary the magnetic field of the coil. This can be done by:
1. Moving the magnet towards the coil with a varying velocity.
2. Changing the plane of the coil through which the magnet moves.
3. Rotating a coil relative to the magnet.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




