
The length of the intercept on y-axis, by circle whose diameter is the line joining the points \[\left( { - {\rm{4}},{\rm{3}}} \right){\rm{ and }}\left( {{\rm{12}}, - {\rm{1}}} \right)\] is
A)\[3\sqrt 2 \]
B)\[\sqrt {13} \]
C)\[4\sqrt {13} \]
D)None of these.
Answer
483.6k+ views
Hint: First find the midpoint of 2 given points which will in turn become the center of the circle as 2 points are the endpoint of diameter. Find distance between 2 points center, any point to get the radius. As you know center and radius find the equation of circle. The y-intercept of the circle in the form of \[{x^2} + {y^2} + 2gx + 2fy + c = 0{\text{ is 2}}\sqrt {{f^2} - c} \].
Complete step by step solution:
The two given points of diameter are written as follows:
\[{\rm{A}}\left( { - {\rm{4}},{\rm{3}}} \right);{\rm{ B}}\left( {{\rm{12}}, - {\rm{1}}} \right)\]
Let the center of the circle be \[O = \left( {x,y} \right)\]point.
By above we can say the following statements:
x coordinate of the point denoted by A is given by -4.
x coordinate of the point denoted by B is given by 12.
x coordinate of the point denoted by O is given by x.
y coordinate of the point denoted by A is given by 3.
y coordinate of the point denoted by B is given by -1.
y coordinate of the point denoted by o is given by y.
The point O is the midpoint of points A, B.
The x coordinate of O is average of x coordinates of A, B, we get:
\[x = {\text{ average of - 4, 12 = }}\dfrac{{12 - 4}}{2}\]
By simplifying we get the value of x to be as:
\[x = 4\]
The y coordinate of O is average of y coordinates of A, B, we get:
\[y = {\text{ average of 3, - 1 = }}\dfrac{{3 - 1}}{2}\]
By simplifying we get the value of y to be as:
\[y = 1\]
So, the center of circle is given by point O \[\left( {{\rm{4}},{\rm{1}}} \right)\]
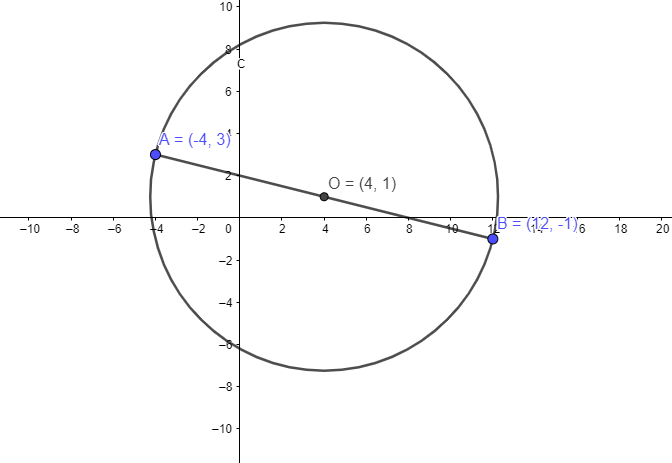
The radius of the circle can be denoted as OA.
The distance between two points (a, b) (c, d) is d, can be given by:
\[d = \sqrt {{{\left( {a - c} \right)}^2} + {{\left( {b - d} \right)}^2}} \]
By substituting the values, we can write value of radius as:
Radius = distance between \[\left( {4,1} \right),\left( { - 4,3} \right) = \sqrt {{{\left( {4 + 4} \right)}^2} + {{\left( {3 - 1} \right)}^2}} \]
By simplifying the above equation we can get value of radius as:
Radius \[ = \sqrt {{8^2} + {2^2}} = \sqrt {64 + 4} = \sqrt {68} \]
Center \[ = \left( {{\rm{4}},{\rm{1}}} \right)\]
If center is (g, f) and radius r, we get equation as:
\[{\left( {x - g} \right)^2} + {\left( {y - f} \right)^2} = {r^2}\]
By substituting the values, we get it as:
\[{\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 68\]
By substituting \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab,\]we get the equation as:
\[{x^2} + 16 - 8x + {y^2} + 1 - 2y = 68\]
By simplifying the above equation, we get final equation as:
\[{x^2} + {y^2} - 8x - 2y - 51 = 0\]
By comparing it to \[{x^2} + {y^2} + 2gx + 2fy + c = 0\], we get:
\[2g = - 8,2f = - 2{\rm{ }} \Rightarrow {\rm{g = - 4,f = - 1,c = - 51}}\]
We know he y intercept given by:
$\text{y-intercept=2}\sqrt{{{f}^{2}}-c}$
By substituting f, c values, we get it as:
$\text{y-intercept=2}\sqrt{1-\left( -51 \right)}=2\sqrt{52}$
52 can be written as \[13 \times 4\]. So, by substituting it we get it as:
y intercept \[ = 4\sqrt {13.} \]
Therefore, option (c) is the correct answer.
Note: Be careful while getting the center as the whole equation of circle depends on that point. Don’t confuse between x, y coordinates. Alternate method is to substitute \[{\rm{x}} = 0\] and get the y values of the circle. Now get 2 intersection points on the y-axis. The distance between the two points is called the y-intercept. Anyway you get the same result.
Complete step by step solution:
The two given points of diameter are written as follows:
\[{\rm{A}}\left( { - {\rm{4}},{\rm{3}}} \right);{\rm{ B}}\left( {{\rm{12}}, - {\rm{1}}} \right)\]
Let the center of the circle be \[O = \left( {x,y} \right)\]point.
By above we can say the following statements:
x coordinate of the point denoted by A is given by -4.
x coordinate of the point denoted by B is given by 12.
x coordinate of the point denoted by O is given by x.
y coordinate of the point denoted by A is given by 3.
y coordinate of the point denoted by B is given by -1.
y coordinate of the point denoted by o is given by y.
The point O is the midpoint of points A, B.
The x coordinate of O is average of x coordinates of A, B, we get:
\[x = {\text{ average of - 4, 12 = }}\dfrac{{12 - 4}}{2}\]
By simplifying we get the value of x to be as:
\[x = 4\]
The y coordinate of O is average of y coordinates of A, B, we get:
\[y = {\text{ average of 3, - 1 = }}\dfrac{{3 - 1}}{2}\]
By simplifying we get the value of y to be as:
\[y = 1\]
So, the center of circle is given by point O \[\left( {{\rm{4}},{\rm{1}}} \right)\]

The radius of the circle can be denoted as OA.
The distance between two points (a, b) (c, d) is d, can be given by:
\[d = \sqrt {{{\left( {a - c} \right)}^2} + {{\left( {b - d} \right)}^2}} \]
By substituting the values, we can write value of radius as:
Radius = distance between \[\left( {4,1} \right),\left( { - 4,3} \right) = \sqrt {{{\left( {4 + 4} \right)}^2} + {{\left( {3 - 1} \right)}^2}} \]
By simplifying the above equation we can get value of radius as:
Radius \[ = \sqrt {{8^2} + {2^2}} = \sqrt {64 + 4} = \sqrt {68} \]
Center \[ = \left( {{\rm{4}},{\rm{1}}} \right)\]
If center is (g, f) and radius r, we get equation as:
\[{\left( {x - g} \right)^2} + {\left( {y - f} \right)^2} = {r^2}\]
By substituting the values, we get it as:
\[{\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 68\]
By substituting \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab,\]we get the equation as:
\[{x^2} + 16 - 8x + {y^2} + 1 - 2y = 68\]
By simplifying the above equation, we get final equation as:
\[{x^2} + {y^2} - 8x - 2y - 51 = 0\]
By comparing it to \[{x^2} + {y^2} + 2gx + 2fy + c = 0\], we get:
\[2g = - 8,2f = - 2{\rm{ }} \Rightarrow {\rm{g = - 4,f = - 1,c = - 51}}\]
We know he y intercept given by:
$\text{y-intercept=2}\sqrt{{{f}^{2}}-c}$
By substituting f, c values, we get it as:
$\text{y-intercept=2}\sqrt{1-\left( -51 \right)}=2\sqrt{52}$
52 can be written as \[13 \times 4\]. So, by substituting it we get it as:
y intercept \[ = 4\sqrt {13.} \]
Therefore, option (c) is the correct answer.
Note: Be careful while getting the center as the whole equation of circle depends on that point. Don’t confuse between x, y coordinates. Alternate method is to substitute \[{\rm{x}} = 0\] and get the y values of the circle. Now get 2 intersection points on the y-axis. The distance between the two points is called the y-intercept. Anyway you get the same result.
Recently Updated Pages
What do you understand by friction Draw a graph between class 11 physics CBSE

What is loading Explain the process of loading with class 11 chemistry CBSE

Electronic energy is negative because A Electron has class 11 chemistry CBSE

The time taken by a particle performing SHM to pass class 11 physics CBSE

How do the lungs help maintain homeostasis in the class 11 biology CBSE

Describe an activity to show that sound requires a class 11 physics CBSE

Trending doubts
The reservoir of dam is called Govind Sagar A Jayakwadi class 11 social science CBSE

What problem did Carter face when he reached the mummy class 11 english CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

In China rose the flowers are A Zygomorphic epigynous class 11 biology CBSE

What is Environment class 11 chemistry CBSE

Nucleolus is present in which part of the cell class 11 biology CBSE




