
The hall effect turned out to be not observable in a semiconductor whose conduction electron mobility was $\eta = 2.0$ times that of the hole mobility. Find the ratio of hole and conduction electron concentrations in that semiconductor.
Answer
436.2k+ views
Hint: Hall effect may not be observable in some materials because conduction can involve significant, simultaneous contributions from both electrons and holes, which may be present in different concentrations and have different mobilities. We should remember the formula of electron mobility and current density to solve this.
Complete step by step solution:
When the sample contains an unequal number of carriers of both types whose mobilities are different, static equilibrium (no transverse movement of either electron or holes) is impossible in a magnetic field. The transverse electric field acts differently on electrons and holes.
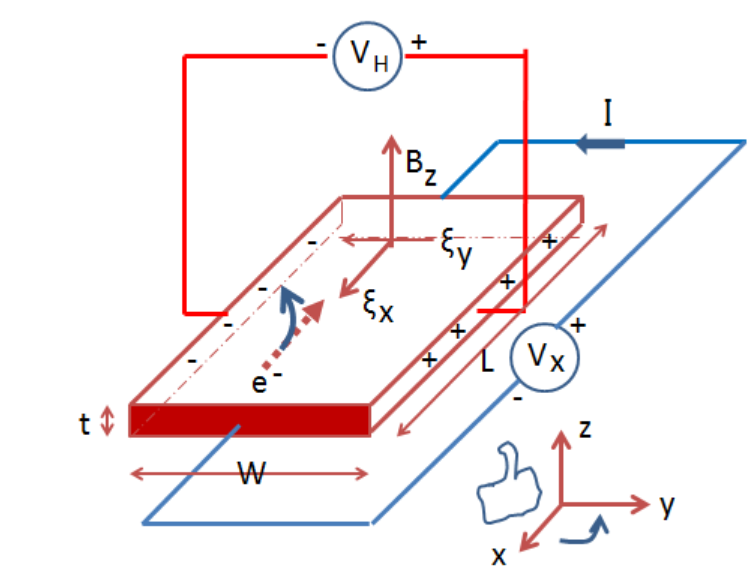
If the ${E_y}$ is an electric field along the y-direction in the presence of the magnetic field $B$. And let the drift velocities of electrons and holes in x-direction be ${v_e}$ and ${v_h}$. The net Lorentz force per unit charge (effective transverse electric field) on electrons is
${E_y} - {v_e}B$
And on holes is
${E_y} + {v_h}B$
Now there is a transverse drift of electrons and holes and the net transverse current must be zero in equilibrium.
Therefore, the sum of the mobilities of the electrons and holes must be zero. Applying that in the mobility equation we get
${\mu _e}{n_e}e({E_y} - {\mu _e}{E_x}B) + {\mu _h}{n_h}e({E_y} + {\mu _h}{E_x}B) = 0$ (since $v = \mu {E_x}$)
Where $\mu $is the mobility, $e$ is the electronic charge and $n$ is the concentration.
Rearranging the equation we get
${E_y} = \dfrac{{{n_e}{\mu _e}^2 - {n_h}{\mu _h}^2}}{{{n_e}{\mu _e} + {n_h}{\mu _h}}}{E_x}B$
And we know the current density $({j_x})$ is
${j_x} = ({n_e}{\mu _e} + {n_h}{\mu _h})e{E_x}$
Thus the Hall coefficient $({R_H})$ is
${R_H} = \dfrac{{{E_y}}}{{{j_x}B}}$
Substituting the values we get
${R_H} = \dfrac{1}{e}\dfrac{{{n_e}{\mu _e}^2 - {n_h}{\mu _h}^2}}{{{{({n_e}{\mu _e} + {n_h}{\mu _h})}^2}}}$
Now since the Hall effect is not observed in the semiconductor the coefficient will be zero.
Therefore equating the above equation to zero we get,
$\dfrac{{{n_e}}}{{{n_h}}} = {\left( {\dfrac{{{\mu _e}}}{{{\mu _h}}}} \right)^2}$
Now $\eta = 0.2$ (given)
Therefore $\dfrac{{{n_e}}}{{{n_h}}} = \dfrac{1}{{{\eta ^2}}}$
$ \Rightarrow \dfrac{{{n_e}}}{{{n_h}}} = \dfrac{1}{4}$
Which is the required ratio.
Note: Hall effect is the production of the voltage difference. It is caused across an electric conductor and is transverse to this electric current. It refers to the product of magnetic induction and current density when a magnetic field works perpendicular to the current flow.
Complete step by step solution:
When the sample contains an unequal number of carriers of both types whose mobilities are different, static equilibrium (no transverse movement of either electron or holes) is impossible in a magnetic field. The transverse electric field acts differently on electrons and holes.

If the ${E_y}$ is an electric field along the y-direction in the presence of the magnetic field $B$. And let the drift velocities of electrons and holes in x-direction be ${v_e}$ and ${v_h}$. The net Lorentz force per unit charge (effective transverse electric field) on electrons is
${E_y} - {v_e}B$
And on holes is
${E_y} + {v_h}B$
Now there is a transverse drift of electrons and holes and the net transverse current must be zero in equilibrium.
Therefore, the sum of the mobilities of the electrons and holes must be zero. Applying that in the mobility equation we get
${\mu _e}{n_e}e({E_y} - {\mu _e}{E_x}B) + {\mu _h}{n_h}e({E_y} + {\mu _h}{E_x}B) = 0$ (since $v = \mu {E_x}$)
Where $\mu $is the mobility, $e$ is the electronic charge and $n$ is the concentration.
Rearranging the equation we get
${E_y} = \dfrac{{{n_e}{\mu _e}^2 - {n_h}{\mu _h}^2}}{{{n_e}{\mu _e} + {n_h}{\mu _h}}}{E_x}B$
And we know the current density $({j_x})$ is
${j_x} = ({n_e}{\mu _e} + {n_h}{\mu _h})e{E_x}$
Thus the Hall coefficient $({R_H})$ is
${R_H} = \dfrac{{{E_y}}}{{{j_x}B}}$
Substituting the values we get
${R_H} = \dfrac{1}{e}\dfrac{{{n_e}{\mu _e}^2 - {n_h}{\mu _h}^2}}{{{{({n_e}{\mu _e} + {n_h}{\mu _h})}^2}}}$
Now since the Hall effect is not observed in the semiconductor the coefficient will be zero.
Therefore equating the above equation to zero we get,
$\dfrac{{{n_e}}}{{{n_h}}} = {\left( {\dfrac{{{\mu _e}}}{{{\mu _h}}}} \right)^2}$
Now $\eta = 0.2$ (given)
Therefore $\dfrac{{{n_e}}}{{{n_h}}} = \dfrac{1}{{{\eta ^2}}}$
$ \Rightarrow \dfrac{{{n_e}}}{{{n_h}}} = \dfrac{1}{4}$
Which is the required ratio.
Note: Hall effect is the production of the voltage difference. It is caused across an electric conductor and is transverse to this electric current. It refers to the product of magnetic induction and current density when a magnetic field works perpendicular to the current flow.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What is transplantation in agriculture class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Hydrological cycle is controlled by A Grasslands B class 12 biology CBSE

Who discovered the cell and how class 12 biology CBSE




