
The Fourier series of an odd periodic function, contains only
(A) Odd harmonics
(B) Even harmonics
(C) Cosine terms
(D) Sine terms
Answer
502.2k+ views
Hint: A Fourier series is a means of representing a periodic function as a sum of sine and cosine functions (possibly infinite).In such problems, finding zero coefficients is time consuming and can be prevented. With understanding of even and odd functions, without implementing the integration, the zero coefficient can be predicted.
Complete step by step answer:
A function $ y = f(t) $ is said to be odd if $ f( - t) = - f(t) $ for all values of $ t $ . The graph of an odd function is always symmetrical about the origin.
Let the odd function be $ f(t) = \sin t $
Then the graph of the following function will be represented as:
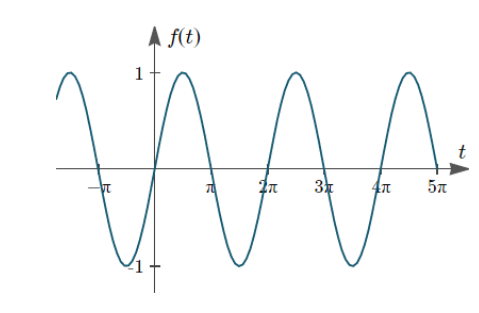
The above graph has amplitude $ 1 $ and period $ 2\pi $
For an odd function $ f(t) $ defined over the range $ - L $ to $ L $ (period $ = 2L) $
We can observe that $ {a_n} = 0 $ for all $ n $
Then we have
$ {a_n} = \dfrac{1}{L}\int_{ - L}^L f (t)\cos \dfrac{{n\pi t}}{L}dt $
So, the zero coefficients in this case are: $ {a_0} = 0 $ and $ {a_n} = 0 $
The coefficients of $ {b_n} $ is given by
$ {b_n} = \dfrac{1}{L}\int_{ - L}^L f (t)\sin \dfrac{{n\pi t}}{L}dt $
Therefore, the Fourier series of the following odd function is given by
$ f(t) = \sum\limits_{n = 1}^\infty {{b_n}} \sin \dfrac{{n\pi t}}{L} $
Hence, the Fourier series of an odd periodic function contains only sine terms.
Hence the correct option is (D).
Note:
Using the Fourier series in various questions makes our task easy, fast, and more productive. We can easily find out the zero coefficient of vast problems by the help of Fourier series even without performing the actual integration. Baron Jean Baptiste Joseph Fourier introduced the idea that a series of harmonically related sines and cosines can represent any periodic function.
Complete step by step answer:
A function $ y = f(t) $ is said to be odd if $ f( - t) = - f(t) $ for all values of $ t $ . The graph of an odd function is always symmetrical about the origin.
Let the odd function be $ f(t) = \sin t $
Then the graph of the following function will be represented as:

The above graph has amplitude $ 1 $ and period $ 2\pi $
For an odd function $ f(t) $ defined over the range $ - L $ to $ L $ (period $ = 2L) $
We can observe that $ {a_n} = 0 $ for all $ n $
Then we have
$ {a_n} = \dfrac{1}{L}\int_{ - L}^L f (t)\cos \dfrac{{n\pi t}}{L}dt $
So, the zero coefficients in this case are: $ {a_0} = 0 $ and $ {a_n} = 0 $
The coefficients of $ {b_n} $ is given by
$ {b_n} = \dfrac{1}{L}\int_{ - L}^L f (t)\sin \dfrac{{n\pi t}}{L}dt $
Therefore, the Fourier series of the following odd function is given by
$ f(t) = \sum\limits_{n = 1}^\infty {{b_n}} \sin \dfrac{{n\pi t}}{L} $
Hence, the Fourier series of an odd periodic function contains only sine terms.
Hence the correct option is (D).
Note:
Using the Fourier series in various questions makes our task easy, fast, and more productive. We can easily find out the zero coefficient of vast problems by the help of Fourier series even without performing the actual integration. Baron Jean Baptiste Joseph Fourier introduced the idea that a series of harmonically related sines and cosines can represent any periodic function.
Recently Updated Pages
NCERT Solutions For Class 4 English Marigold - Alice In Wonderland

NCERT Solutions For Class 5 English Marigold (Poem) - Nobody's Friend

NCERT Solutions For Class 6 Hindi Durva - Angulimaal

NCERT Solutions For Class 6 Hindi Bal Ram Katha - Lanka Vijay

NCERT Solutions For Class 11 Physics In Hindi - Mechanical Properties of Fluids

Adjective Worksheets for Kids: Printable Grammar Practice

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




