Question

The elastic limit of an elevator cable is $2\times 10^{9} \dfrac{N}{m^2 }$ . The maximum upward acceleration that an elevator of mass $2\times 10^3 $kg can have when supported by a cable whose cross-sectional area is $10^{-4}$ provided the stress in the cable would not exceed half of the elastic limit would be:
A.) 10 $ms^{-2}$
B.) 50 $ms^{-2}$
C.) 40 $ms^{-2}$
D.) Not possible to move up

Answer 1

Hint: Make a free body diagram of the elevator and calculate the net force acting on the elevator. Calculate the maximum stress possible and hence the maximum force possible and apply the condition to the expression for the net force acting on the elevator to get max possible acceleration.

Complete step-by-step answer:
The given elastic limit of the elevator cable is $2\times 10^{9} N/m^2$
the area of cross-section of elevator cable is $10^{-4}m^2$
The mass of the elevator is $2\times 10^3$ kg
The free body diagram of the elevator can be drawn as

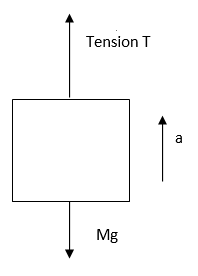
We are given the stress in the cable should not exceed half of the elastic limit of the cable so we get
We know the stress is given by $stress= \alpha = \dfrac{Tension}{Area} = \dfrac{T}{A} = \dfrac{m(g+a)}{a}$

We get from the given condition :

$\begin{align}
  & \alpha =\dfrac{m(g+a)}{A}\le \dfrac{{{\alpha }_{max}}}{2}=\dfrac{2\times {{10}^{9}}}{2} \\
 & g+a\le \dfrac{2\times 9}{2}\dfrac{{{10}^{-4}}}{2\times {{10}^{3}}}=50 \\
 & a\le 50-10=40\dfrac{m}{{{s}^{2}}} \\
\end{align}$

Thus, using the free body diagram and calculating the net force acting on the elevator and the tension in the cable we got the maximum acceleration possible for the elevator as $40 \dfrac{m}{s^2}$.

Additional Information:
The net force acting on the elevator is equal to mass times the upward acceleration of the elevator as it is moving upward. Now we have seen that the net force in the upward direction is nothing but the T – mg where T is the tension in the rope. Hence we have equated this to the ma. So we get the equation T-mg = ma which gives us T = m(g+a) which we used in the problem.

Note: The possible mistake one can do in this kind of problem is that while taking the forces acting on the elevator. One should be able to differentiate between the forces acting on the body and the forces applied by the body on the cable.