
The beam and pans of a balance have negligible mass. An object weighs \[{W_1}\] when placed in one pan and \[{W_2}\] when placed in the other pan. the weight W of the object is:
A.\[\sqrt {{W_1}{W_2}} \]
B. \[\sqrt {\left( {{W_1} + {W_2}} \right)} \]
C. \[{W_1}^2 + {W_2}^2\]
D. \[\dfrac{{{W_1}^{ - 1} + {W_2}^{ - 1}}}{2}\]
Answer
387.3k+ views
Hint: In order to answer this question, we need to understand that a beam balance is working on basis of the principle of moments according to which in the equilibrium, the anti-clockwise moment because of the weight of an object on left pan of the beam is similar to the clockwise moment because of to the standard weights on the right pan of the beam.
Complete step by step answer:
Here, \[{W_1}\] is the object weighed when placed in one pan. \[{W_2}\] is the object weighed when placed in another pan.As pan and beam are weightless, error must be in length of beams. So, both pans are at different distances from support. Let the beam on the left be \[{l_1}\] and the beam on right be \[{l_2}\]. Suppose we put weight W in pan 1, then weight reads \[{W_1}\] that means, weight in pan 2 is \[{W_2}\].
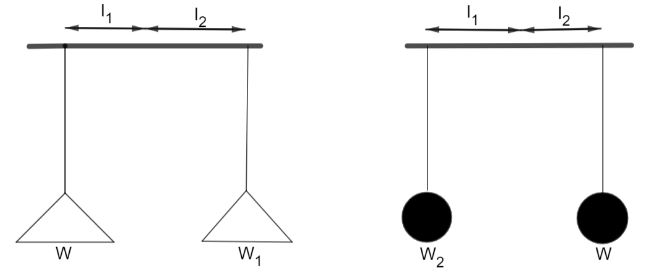
So, \[{\text{ }}W{l_1} = {W_1}{l_2} - - - (1)\]
Now when weight W is kept in pan 2, it reads \[{W_2}\] so weight in pan 1 now is \[{W_1}\]
\[So,{\text{ }}{W_2}{l_1} = W{l_2} - - - (2)\]
Now, dividing equation (1) and (2) we get,
\[\dfrac{{W{l_1}}}{{{W_2}{l_1}}} = \dfrac{{{W_1}{l_2}}}{{W{l_2}}}\]
\[\Rightarrow \dfrac{W}{{{W_2}}} = \dfrac{{{W_1}}}{W}\]
Cross multiplying, we get
\[{W^2} = {W_1}{W_2}\]
\[\therefore W = \sqrt {{W_1}{W_2}} \]
Hence, the correct option is (A).
Note: It should be remembered that when a system is in stability or balance, then it is said to be in equilibrium as all the forces experiencing on the system cancel each other out. Common balance is defined as the balance which is having each arm as suspended. The unknown mass is kept in one arm and the known mass in another until they both become equivalent. Therefore, this balance is working on the principle of moment of weights. When the weights are being balanced, equilibrium is attained.
Complete step by step answer:
Here, \[{W_1}\] is the object weighed when placed in one pan. \[{W_2}\] is the object weighed when placed in another pan.As pan and beam are weightless, error must be in length of beams. So, both pans are at different distances from support. Let the beam on the left be \[{l_1}\] and the beam on right be \[{l_2}\]. Suppose we put weight W in pan 1, then weight reads \[{W_1}\] that means, weight in pan 2 is \[{W_2}\].

So, \[{\text{ }}W{l_1} = {W_1}{l_2} - - - (1)\]
Now when weight W is kept in pan 2, it reads \[{W_2}\] so weight in pan 1 now is \[{W_1}\]
\[So,{\text{ }}{W_2}{l_1} = W{l_2} - - - (2)\]
Now, dividing equation (1) and (2) we get,
\[\dfrac{{W{l_1}}}{{{W_2}{l_1}}} = \dfrac{{{W_1}{l_2}}}{{W{l_2}}}\]
\[\Rightarrow \dfrac{W}{{{W_2}}} = \dfrac{{{W_1}}}{W}\]
Cross multiplying, we get
\[{W^2} = {W_1}{W_2}\]
\[\therefore W = \sqrt {{W_1}{W_2}} \]
Hence, the correct option is (A).
Note: It should be remembered that when a system is in stability or balance, then it is said to be in equilibrium as all the forces experiencing on the system cancel each other out. Common balance is defined as the balance which is having each arm as suspended. The unknown mass is kept in one arm and the known mass in another until they both become equivalent. Therefore, this balance is working on the principle of moment of weights. When the weights are being balanced, equilibrium is attained.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




