
Refractive index of a rectangular glass slab is $ m = \sqrt 3 $ . A light ray at an angle is $ 60^\circ $ displaced laterally through $ 2.5cm $ . Distance travelled by the light in slab is:
(A) $ 4cm $
(B) $ 5cm $
(C) $ 2.5\sqrt 3 cm $
(D) $ 3cm $
Answer
474.9k+ views
Hint :Refractive index, also called index of refraction, measure of the bending of a ray of light when passing from one medium into another. The refractive index $ m $ is defined as the ratio of the sine of the angle of incidence to the sine of the angle of refraction; i.e. Snell’s law $ \dfrac{{\sin i}}{{\sin r}} = m $ where, $ i $ is angle of incidence and $ r $ is angle of refraction.
Complete Step By Step Answer:
We have given the refractive index of slab, angle of incidence and the lateral displacement. We know that when the perpendicular distance between the original path traced by an incident ray and the path traced by the emergent ray coming out from the glass slab is known as lateral displacement. Now, we have to find the distance travelled by light in the slab.
We have the following diagram according to the question:
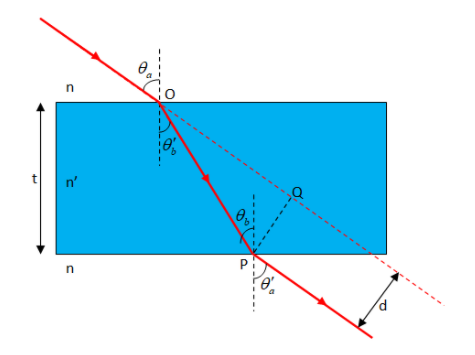
Given,
Refractive index of glass, $ m = \sqrt 3 $
Angle of incidence, $ {\theta _a} = {60^\circ } $
Lateral displacement, $ d = 2.5cm $
To find distance travelled by light in the slab $ OP,l = ? $
Here from Snell’s law we have:
$ \dfrac{{\sin {\theta _a}}}{{\sin \theta _b'}} = m $
Substituting values we get,
$ \Rightarrow \dfrac{{\sin 60^\circ }}{{\sin \theta _b'}} = \sqrt 3 $
$ \Rightarrow \sin \theta _b' = \dfrac{{\sin 60^\circ }}{{\sqrt 3 }} $
From trigonometric ratio we get,
$ \Rightarrow \sin \theta _b' = \dfrac{{\left( {\dfrac{{\sqrt 3 }}{2}} \right)}}{{\sqrt 3 }} $
Simplifying we get,
$ \Rightarrow \sin \theta _b' = \dfrac{1}{2} $
And so,
$ \theta _b' = 30^\circ $
From geometry we have,
$ \angle QOP = {\theta _a} - \theta _b' $
i.e. $ \angle QOP = 60^\circ - 30^\circ = 30^\circ $
Now, we have to find the length $ OP $ which we will find by $ \vartriangle OQP $ using $ \angle QOP $ and $ PQ = d $ applying trigonometric ratio
Let the length travelled by light in glass be $ l $ .
From $ \vartriangle OQP $ we have $ \angle OQP = 90^\circ $ and $ PQ = d = 2.5cm $
And hence we have from trigonometric ratio,
$ Sin\angle QOP = \dfrac{{QP}}{{OP}} $
Putting respective values we get,
$ \Rightarrow \sin 30^\circ = \dfrac{{2.5}}{l} $
Simplifying further
$ \Rightarrow l = \dfrac{{2.5}}{{\sin 30^\circ }} $
$ \Rightarrow l = \dfrac{{2.5}}{{\left( {\dfrac{1}{2}} \right)}}cm $
$ \Rightarrow l = 2.5 \times 2cm $
$ \Rightarrow l = 5cm $
Hence option B is correct.
Note :
Formula for refractive index and idea of trigonometry is must for solving such questions comfortably. Diagrams are must for such types of questions as it gives a clear understanding. One should keep in mind that similar types of questions could be asked by changing the refractive index or the medium of travel of light. Also the incidence angle could be changed a bit which may lead calculation errors.
Complete Step By Step Answer:
We have given the refractive index of slab, angle of incidence and the lateral displacement. We know that when the perpendicular distance between the original path traced by an incident ray and the path traced by the emergent ray coming out from the glass slab is known as lateral displacement. Now, we have to find the distance travelled by light in the slab.
We have the following diagram according to the question:

Given,
Refractive index of glass, $ m = \sqrt 3 $
Angle of incidence, $ {\theta _a} = {60^\circ } $
Lateral displacement, $ d = 2.5cm $
To find distance travelled by light in the slab $ OP,l = ? $
Here from Snell’s law we have:
$ \dfrac{{\sin {\theta _a}}}{{\sin \theta _b'}} = m $
Substituting values we get,
$ \Rightarrow \dfrac{{\sin 60^\circ }}{{\sin \theta _b'}} = \sqrt 3 $
$ \Rightarrow \sin \theta _b' = \dfrac{{\sin 60^\circ }}{{\sqrt 3 }} $
From trigonometric ratio we get,
$ \Rightarrow \sin \theta _b' = \dfrac{{\left( {\dfrac{{\sqrt 3 }}{2}} \right)}}{{\sqrt 3 }} $
Simplifying we get,
$ \Rightarrow \sin \theta _b' = \dfrac{1}{2} $
And so,
$ \theta _b' = 30^\circ $
From geometry we have,
$ \angle QOP = {\theta _a} - \theta _b' $
i.e. $ \angle QOP = 60^\circ - 30^\circ = 30^\circ $
Now, we have to find the length $ OP $ which we will find by $ \vartriangle OQP $ using $ \angle QOP $ and $ PQ = d $ applying trigonometric ratio
Let the length travelled by light in glass be $ l $ .
From $ \vartriangle OQP $ we have $ \angle OQP = 90^\circ $ and $ PQ = d = 2.5cm $
And hence we have from trigonometric ratio,
$ Sin\angle QOP = \dfrac{{QP}}{{OP}} $
Putting respective values we get,
$ \Rightarrow \sin 30^\circ = \dfrac{{2.5}}{l} $
Simplifying further
$ \Rightarrow l = \dfrac{{2.5}}{{\sin 30^\circ }} $
$ \Rightarrow l = \dfrac{{2.5}}{{\left( {\dfrac{1}{2}} \right)}}cm $
$ \Rightarrow l = 2.5 \times 2cm $
$ \Rightarrow l = 5cm $
Hence option B is correct.
Note :
Formula for refractive index and idea of trigonometry is must for solving such questions comfortably. Diagrams are must for such types of questions as it gives a clear understanding. One should keep in mind that similar types of questions could be asked by changing the refractive index or the medium of travel of light. Also the incidence angle could be changed a bit which may lead calculation errors.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What is transplantation in agriculture class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Who discovered the cell and how class 12 biology CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?




