
Phase difference between voltage and current in a capacitor in an ac circuit is then
$\begin{gathered}
{\text{A}}{\text{. }}\pi \\
{\text{B}}{\text{. }}\dfrac{\pi }{2} \\
{\text{C}}{\text{. 0}} \\
{\text{D}}{\text{. }}\dfrac{\pi }{3} \\
\end{gathered} $
Answer
582.6k+ views
Hint: When we use a capacitor in an ac circuit, it is observed that the voltage and the current are not in phase with each other. The phase difference between the voltage and current can be calculated by comparing the expressions for voltage and current for a capacitor in an ac circuit.
Formula used:
We know that the charge in a capacitor is given as
$Q = CV$
Here Q is the charge stored in the capacitor, C represents the capacitance of the capacitor while V is the voltage for the capacitor.
We know that the current is given as
$I = \dfrac{{dQ}}{{dt}}$
Therefore, for a capacitor we have
$I = C\dfrac{{dV}}{{dt}}{\text{ }}...{\text{(i)}}$
Detailed step by step solution:
Consider that we have a voltage signal given as follows which is fed to an ac circuit containing capacitor.
It is given as
$V = {V_0}\sin \omega t{\text{ }}...{\text{(a)}}$
Now we can calculate the current in the circuit using the equation (i) in the following way.
$\begin{gathered}
I = C\dfrac{{dV}}{{dt}} \\
= C\dfrac{d}{{dt}}\left( {{V_0}\sin \omega t} \right) \\
= C{V_0}\omega \cos \omega t \\
\end{gathered} $
This expression for current can also be written in the following way:
$I = C{V_0}\omega \sin \left( {\omega t + \dfrac{\pi }{2}} \right){\text{ }}...{\text{(b)}}$
Now when we compare the equation (b) with equation (a), we notice that the voltage is lagging behind the current in the current. The lag is equal to $\dfrac{\pi }{2}$ radians. Hence, the correct answer is option B.
Note: We can also draw a diagram called phasor diagram which represents the phase difference between current and voltage graphically.
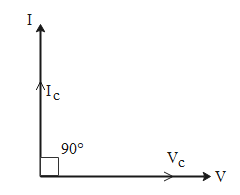
In this diagram we represent the voltage along the x-axis and the current is represented along the y-axis. If we take the voltage in the capacitor to be along the x-axis then since there is a phase difference of 90$^\circ $ between current and voltage, the current is represented along the y-axis at an angle of 90$^\circ $ with respect to the voltage.
Formula used:
We know that the charge in a capacitor is given as
$Q = CV$
Here Q is the charge stored in the capacitor, C represents the capacitance of the capacitor while V is the voltage for the capacitor.
We know that the current is given as
$I = \dfrac{{dQ}}{{dt}}$
Therefore, for a capacitor we have
$I = C\dfrac{{dV}}{{dt}}{\text{ }}...{\text{(i)}}$
Detailed step by step solution:
Consider that we have a voltage signal given as follows which is fed to an ac circuit containing capacitor.

It is given as
$V = {V_0}\sin \omega t{\text{ }}...{\text{(a)}}$
Now we can calculate the current in the circuit using the equation (i) in the following way.
$\begin{gathered}
I = C\dfrac{{dV}}{{dt}} \\
= C\dfrac{d}{{dt}}\left( {{V_0}\sin \omega t} \right) \\
= C{V_0}\omega \cos \omega t \\
\end{gathered} $
This expression for current can also be written in the following way:
$I = C{V_0}\omega \sin \left( {\omega t + \dfrac{\pi }{2}} \right){\text{ }}...{\text{(b)}}$
Now when we compare the equation (b) with equation (a), we notice that the voltage is lagging behind the current in the current. The lag is equal to $\dfrac{\pi }{2}$ radians. Hence, the correct answer is option B.
Note: We can also draw a diagram called phasor diagram which represents the phase difference between current and voltage graphically.

In this diagram we represent the voltage along the x-axis and the current is represented along the y-axis. If we take the voltage in the capacitor to be along the x-axis then since there is a phase difference of 90$^\circ $ between current and voltage, the current is represented along the y-axis at an angle of 90$^\circ $ with respect to the voltage.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Differentiate between action potential and resting class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




