Question

What is the maximum height of a projectile?

Answer 1

Hint: Firstly, write the velocity vector, thereafter apply the third equation of motion and put values of various quantities in the equation at maximum height for the projectile. Remember that in a projectile at maximum height, velocity has only x-component.

Complete step by step answer:
Let the projectile move with initial velocity u, which makes an angle \[\text{ }\!\!\theta\!\!\text{ }\] with the horizontal.

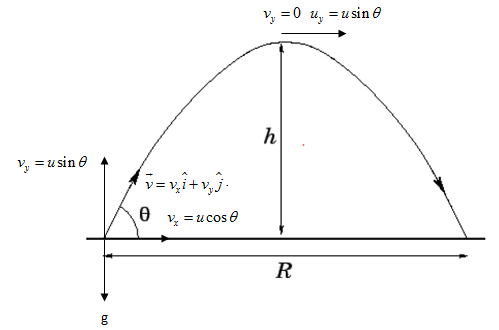
Now the velocity vector after time t is given by,

\[\overrightarrow{v}={{v}_{x}}\widehat{i}+{{v}_{y}}\widehat{j}\]--------(1)
\[\overrightarrow{v}=(u\cos \theta )\widehat{i}+\left( u\sin \theta -gt \right)\widehat{j}\]

As we know that in a projectile at maximum height, velocity has only x-component.

i.e., \[{{v}_{x}}=u\cos \theta \]

Now by using third equation of motion,

\[{{v}_{y}}^{2}={{u}_{y}}^{2}+2{{a}_{y}}h\] --------(2)

In case of projectile motion at maximum height,

\[{{v}_{y}}=0\]
\[{{u}_{y}}=u\sin \theta \]
\[{{a}_{y}}=-g\]
\[h={{h}_{\max .}}\]

Putting the above values in equation (2),

\[0={{\left( u\sin \theta \right)}^{2}}-2g{{h}_{\max .}}\]
\[\Rightarrow {{\left( u\sin \theta \right)}^{2}}=2g{{h}_{\max .}}\]
\[\Rightarrow {{h}_{\max .}}=\dfrac{{{\left( u\sin \theta \right)}^{2}}}{2g}\]
Or, \[{{h}_{\max .}}=\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\]

Therefore, the maximum height of projectile is given by, \[{{h}_{\max .}}=\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\]

Additional Information:
Projectile motion is the motion of an object thrown or projected into the air, only under the gravitational acceleration. There are many uses of projectile motion in mechanics. Such objects are called projectiles and their path is called a trajectory. We consider two-dimensional projectile motion, and we neglect the effects of air resistance.
The most important fact to remember here is that motions along perpendicular axes are independent and thus we can analyse them separately. The method to analyse two-dimensional projectile motion is to break it into two motions: one along the horizontal axis and the other along the vertical axis.

Note: Students should avoid confusion with the concept that the only force acting upon an upward moving projectile is gravity. Their conception of motion encourages them to think that if an object is moving upward, then there must be an upward force and if an object is moving upward and rightward, there must be both an upward and rightward force.