
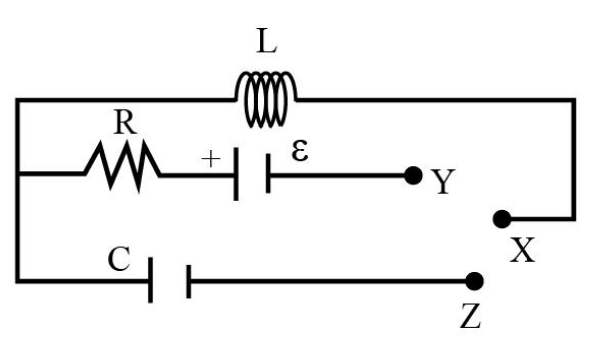
In the circuit shown, the symbols have their usual meanings. The cell has emf $\varepsilon $. $X$ is initially joined to $Y$ for a long time. Then, $X$ is joined to $Z$. The maximum charge on $C$ at any later time will be
A. $\dfrac{\varepsilon }{{R\sqrt {LC} }}$
B. $\dfrac{{\varepsilon R}}{{2\sqrt {LC} }}$
C. $\dfrac{{\varepsilon \sqrt {LC} }}{R}$
D. $\dfrac{{\varepsilon \sqrt {LC} }}{{2R}}$

Answer
511.8k+ views
Hint:To give the answer this problem we must know about the concept of LC circuit. In this problem first we determine the current flow through the circuit, then find the energy stored, and charge in the circuit, and finally apply the law of conservation of energy to obtain the required result.
Complete step by step answer:
In the given circuit, the $L$ represents the inductance, $R$ represents the resistance, and $C$ represents the capacitance.When initially the circuit is connected with $Y$ then the charge is started to store in inductance, and at the steady state the current flow through the circuit will be as follows.
$i = \dfrac{\varepsilon }{R}$
The energy stored at the steady state will be as follows.
\[E = \dfrac{1}{2}L{i^2}\]
When the circuit is connected with $Z$ then it will become an LC circuit. As we know that in LC circuits oscillation occurs. In the oscillation if the $L$ is fully charged initially then energy transferred to $C$ and when $C$ is completely charged then it slowly starts discharging and the process charging and discharging of $L$ and $C$ is going on in LC circuit.The charge stored in $LC$ circuit will be maximum only when energy is maximum in that circuit.
The charge stored in the circuit is given by,
${\rm{Charge}}\;{\rm{stored}} = \dfrac{{{Q^2}}}{{2C}}$
From the conservation of energy,
\[
\dfrac{1}{2}L{i^2} = \dfrac{{{Q^2}}}{{2C}}\\
Q = i\sqrt {LC}
\]
By substituting $\dfrac{\varepsilon }{R}$ for $i$ in the equation \[Q = i\sqrt {LC} \], we get,
\[\therefore Q = \dfrac{\varepsilon }{R}\sqrt {LC} \]
Therefore, the option C is the correct answer.
Note:The key concept of this problem is that initially there was no energy in the capacitor, so, by the law of conservation of energy, the energy stored in the $L$ will be equal to the charge stored in $C$.
Complete step by step answer:
In the given circuit, the $L$ represents the inductance, $R$ represents the resistance, and $C$ represents the capacitance.When initially the circuit is connected with $Y$ then the charge is started to store in inductance, and at the steady state the current flow through the circuit will be as follows.
$i = \dfrac{\varepsilon }{R}$
The energy stored at the steady state will be as follows.
\[E = \dfrac{1}{2}L{i^2}\]
When the circuit is connected with $Z$ then it will become an LC circuit. As we know that in LC circuits oscillation occurs. In the oscillation if the $L$ is fully charged initially then energy transferred to $C$ and when $C$ is completely charged then it slowly starts discharging and the process charging and discharging of $L$ and $C$ is going on in LC circuit.The charge stored in $LC$ circuit will be maximum only when energy is maximum in that circuit.
The charge stored in the circuit is given by,
${\rm{Charge}}\;{\rm{stored}} = \dfrac{{{Q^2}}}{{2C}}$
From the conservation of energy,
\[
\dfrac{1}{2}L{i^2} = \dfrac{{{Q^2}}}{{2C}}\\
Q = i\sqrt {LC}
\]
By substituting $\dfrac{\varepsilon }{R}$ for $i$ in the equation \[Q = i\sqrt {LC} \], we get,
\[\therefore Q = \dfrac{\varepsilon }{R}\sqrt {LC} \]
Therefore, the option C is the correct answer.
Note:The key concept of this problem is that initially there was no energy in the capacitor, so, by the law of conservation of energy, the energy stored in the $L$ will be equal to the charge stored in $C$.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What is transplantation in agriculture class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Hydrological cycle is controlled by A Grasslands B class 12 biology CBSE

Who discovered the cell and how class 12 biology CBSE




