
In amplitude modulation, sinusoidal carrier frequency used is denoted by ${\omega _c}$ and the signal frequency is denoted by ${\omega _m}$. The bandwidth ($\Delta {\omega _m}$) of the signal is such that, $\Delta {\omega _m} < < {\omega _c}$. The frequency not contained in the modulated wave is then,
(A) ${\omega _c} - {\omega _m}$
(B) ${\omega _m}$
(C) ${\omega _c}$
(D) ${\omega _m} + {\omega _c}$
Answer
540.9k+ views
Hint: The amplitude modulation is modulation of a wave by varying its amplitude. In amplitude modulation, the amplitude of the carrier wave is varied in proportion to that of the message signal being transmitted. The modulation wave has namely three frequencies f1, f2 and f3 corresponding to $({\omega _c} + {\omega _m})$, ${\omega _c}$ and $({\omega _c} - {\omega _m})$ in terms of angular frequencies. ${\omega _c}$ is the carrier wave frequency, $({\omega _c} + {\omega _m})$ is the upper side band frequency and $({\omega _c} - {\omega _m})$ lower side band frequency.
If the bandwidth $\left( {\Delta {\omega _m}} \right)$ of the signal is such that $\Delta {\omega _m} < < {\omega _c}$, then the frequency spectrum lies within $({\omega _c} + {\omega _m})$,${\omega _c}$ and $({\omega _c} - {\omega _m})$.
Complete step by step solution:
Given,
The sinusoidal carrier frequency is ${\omega _c}$.
The signal frequency is ${\omega _m}$.
The bandwidth is given as $\Delta {\omega _m} < < {\omega _c}$.
Here, $({\omega _c} - {\omega _m})$ is called the lower side frequency band and $({\omega _c} + {\omega _m})$ is called upper side frequency band. The modulated wave consists of the carrier wave frequency ${\omega _c}$ and addition and subtraction of the signal frequency in the side bands. The frequency spectrum is shown in the figure below.
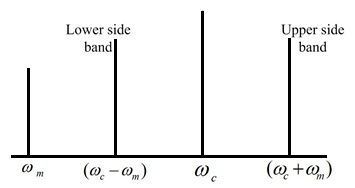
It can be observed that the frequency of the modulated wave lie between $({\omega _c} + {\omega _m})$ and $({\omega _c} - {\omega _m})$ but ${\omega _m}$ does not lie in between the spectrum. It means the frequency which is not contained in the modulated wave is ${\omega _m}$.
Hence, the correct answer is (B).
Note: The students have to understand the amplitude modulation and the frequency corresponding to in amplitude modulation. The frequency of the carrier waves and the modulated wave lies in between a band called upper sideband and lower side band. One can also obtain the answer from the frequency spectrum graph of the amplitude modulated wave.
If the bandwidth $\left( {\Delta {\omega _m}} \right)$ of the signal is such that $\Delta {\omega _m} < < {\omega _c}$, then the frequency spectrum lies within $({\omega _c} + {\omega _m})$,${\omega _c}$ and $({\omega _c} - {\omega _m})$.
Complete step by step solution:
Given,
The sinusoidal carrier frequency is ${\omega _c}$.
The signal frequency is ${\omega _m}$.
The bandwidth is given as $\Delta {\omega _m} < < {\omega _c}$.
Here, $({\omega _c} - {\omega _m})$ is called the lower side frequency band and $({\omega _c} + {\omega _m})$ is called upper side frequency band. The modulated wave consists of the carrier wave frequency ${\omega _c}$ and addition and subtraction of the signal frequency in the side bands. The frequency spectrum is shown in the figure below.

It can be observed that the frequency of the modulated wave lie between $({\omega _c} + {\omega _m})$ and $({\omega _c} - {\omega _m})$ but ${\omega _m}$ does not lie in between the spectrum. It means the frequency which is not contained in the modulated wave is ${\omega _m}$.
Hence, the correct answer is (B).
Note: The students have to understand the amplitude modulation and the frequency corresponding to in amplitude modulation. The frequency of the carrier waves and the modulated wave lies in between a band called upper sideband and lower side band. One can also obtain the answer from the frequency spectrum graph of the amplitude modulated wave.
Recently Updated Pages
Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

What is the opposite of entropy class 11 chemistry CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




