Question

In a series resonant LCR circuit, the voltage across R is 100 volts and \[R=1\Omega \] with \[C=2\mu F\]. The resonant frequency \[\omega \] is \[200\,{rad}/{s}\;\]. At resonance, the voltage across L is:
\[\begin{align}
  & A\,.\,\,4\times {{10}^{-3}}\,volt \\
 & B.\,\,2.5\times {{10}^{-2}}\,volt \\
 & C.\,\,250\,volt \\
 & D.\,\,2.5\times {{10}^{5}}\,volt \\
\end{align}\]

Answer 1

Hint: Firstly, we will compute the value of the current by dividing the voltage value by the resistance. Then, we will divide this current value by the product of the capacitance and the angular frequency to obtain the voltage across the inductor, as, at resonance, the voltage across the inductor equals the voltage across the capacitor.

Formula used:
\[\begin{align}
  & I=\dfrac{V}{R} \\
 & V=\dfrac{I}{C\omega } \\
\end{align}\]

Complete step-by-step answer:
The circuit diagram of the LCR circuit.

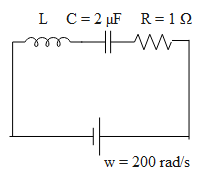
There are two methods to solve this problem.
Direct method
Firstly, we will compute the value of the current using Ohm’s law.
\[I=\dfrac{V}{R}\]
Substitute the values in the formula.
\[\begin{align}
  & I=\dfrac{100}{1000} \\
 & \Rightarrow I=0.1\,A \\
\end{align}\]
The voltage across the inductor equals the voltage across the capacitor. \[{{V}_{L}}={{V}_{C}}\]
Therefore, the voltage across the inductor is,
\[V=\dfrac{I}{\omega C}\]
Substitute the values in the formula.
\[\begin{align}
  & V=\dfrac{0.1}{200\times 2\times {{10}^{-6}}} \\
 & \Rightarrow V=250V \\
\end{align}\]
\[\therefore \]The value of the voltage across L, is \[250\,V\], thus, the option (C) is correct.

Note:
Alternate solution:
The formula for computing the current flowing through an LCR circuit is given as follows.
\[I=\dfrac{E}{Z}\]
Where \[E\]is the emf and \[Z\]is the reactance.
Here, the emf equals, \[E=\sqrt{V_{R}^{2}+{{({{V}_{L}}-{{V}_{C}})}^{2}}}\]and the reactance equals, \[Z=\sqrt{{{R}^{2}}+{{({{X}_{L}}-{{X}_{C}})}^{2}}}\].
At resonance, the capacitive reactance equals the inductive reactance. So, we have, \[{{X}_{L}}={{X}_{C}}\].
Thus, the resistance of the circuit equals the reactance of the circuit, that is, \[Z=R\].
 Again at resonance, the voltage across the capacitor equals the voltage across the inductor. So, we get, \[{{V}_{L}}={{V}_{C}}\].
Thus, the emf of the circuit equals the voltage across the circuit, that is, \[E={{V}_{R}}\].
Therefore, the current is computed as follows.
\[I=\dfrac{{{V}_{R}}}{R}\]
Substitute the values in the formula.
\[\begin{align}
  & I=\dfrac{100}{1000} \\
 & \Rightarrow I=0.1\,A \\
\end{align}\]
The voltage across the inductor is given by the formula as follows.
\[\begin{align}
  & {{V}_{L}}=IL\omega \\
 & \Rightarrow {{V}_{L}}=\dfrac{I}{C\omega } \\
\end{align}\]
Substitute the values in the formula.
\[\begin{align}
  & {{V}_{L}}=\dfrac{0.1}{200\times 2\times {{10}^{-6}}} \\
 & \Rightarrow {{V}_{L}}=250V \\
\end{align}\]
\[\therefore \]The value of the voltage across L, is \[250\,V\]
So, the correct answer is “Option C”.

The Alternate solution is the elaborated version of the direct method. In this problem, as the value of the inductor is used, so, the inductive reactance value is used, if in case, they ask for the capacitance value, then, the capacitive reactance should be used.