
In a series LCR AC circuit, the current is maximum when the impedance is equal to:
A. the reactance
B. the resistance
C. zero
D. twice the reactance
E. twice the resistance
Answer
471.3k+ views
Hint: The resistance is the property of the resistor to resist the flow of current through the circuit. The inductive reactance is the resistance offered by the inductor. The capacitive reactance is the resistance offered by the capacitor. The current is the emf by the impedance.
Complete step-by-step solution:
The properties of the electrical components used to solve this problem are: The resistance is the property of the resistor to resist the flow of current through the circuit. The inductive reactance is the resistance offered by the inductor. The capacitive reactance is the resistance offered by the capacitor. In general, the overall capacitive reactance and the inductive reactance is simply called the reactance.
According to Ohm’s law, the current is voltage by the resistance. In the case of the AC circuit, the current is the emf by the impedance. Here, the impedance equals the root of the sum of the squares of resistance and the (difference/sum of the inductive and the capacitive reactance).
Consider the circuit diagram.
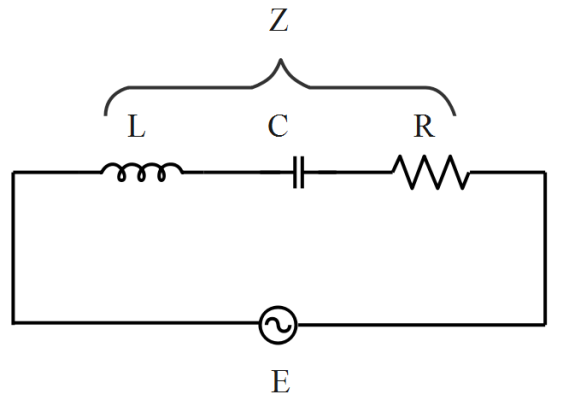
According to Ohm’s law, the relation between the current, voltage and impedance is,
\[I=\dfrac{E}{Z}\]
Where I is the current, E is the emf and Z is the total impedance.
The mathematical representation of the same is given as follows.
\[I=\dfrac{{{E}_{0}}}{\sqrt{{{R}^{2}}+{{\left( {{X}_{L}}-{{X}_{C}} \right)}^{2}}}}\]
When the inductive reactance equals the capacitive reactance, we get,
\[\begin{align}
& I=\dfrac{{{E}_{0}}}{\sqrt{{{R}^{2}}+{{\left( {{X}_{L}}-{{X}_{L}} \right)}^{2}}}} \\
& \Rightarrow I=\dfrac{{{E}_{0}}}{\sqrt{{{R}^{2}}}} \\
& \therefore I=\dfrac{{{E}_{0}}}{R} \\
\end{align}\]
As the above equation has a smaller denominator value, thus, the maximum amount of current will flow.
\[\therefore \] In a series LCR AC circuit, the current is maximum when the impedance is equal to the resistance, thus, option (B) is correct.
Note: In the case of a capacitor, voltage lags current by \[90{}^\circ \]. In the case of an inductor, voltage leads current by \[90{}^\circ \]. Therefore, the voltages on the inductor and capacitor are \[180{}^\circ \]out of phase with each other so they have to be subtracted.
Complete step-by-step solution:
The properties of the electrical components used to solve this problem are: The resistance is the property of the resistor to resist the flow of current through the circuit. The inductive reactance is the resistance offered by the inductor. The capacitive reactance is the resistance offered by the capacitor. In general, the overall capacitive reactance and the inductive reactance is simply called the reactance.
According to Ohm’s law, the current is voltage by the resistance. In the case of the AC circuit, the current is the emf by the impedance. Here, the impedance equals the root of the sum of the squares of resistance and the (difference/sum of the inductive and the capacitive reactance).
Consider the circuit diagram.

According to Ohm’s law, the relation between the current, voltage and impedance is,
\[I=\dfrac{E}{Z}\]
Where I is the current, E is the emf and Z is the total impedance.
The mathematical representation of the same is given as follows.
\[I=\dfrac{{{E}_{0}}}{\sqrt{{{R}^{2}}+{{\left( {{X}_{L}}-{{X}_{C}} \right)}^{2}}}}\]
When the inductive reactance equals the capacitive reactance, we get,
\[\begin{align}
& I=\dfrac{{{E}_{0}}}{\sqrt{{{R}^{2}}+{{\left( {{X}_{L}}-{{X}_{L}} \right)}^{2}}}} \\
& \Rightarrow I=\dfrac{{{E}_{0}}}{\sqrt{{{R}^{2}}}} \\
& \therefore I=\dfrac{{{E}_{0}}}{R} \\
\end{align}\]
As the above equation has a smaller denominator value, thus, the maximum amount of current will flow.
\[\therefore \] In a series LCR AC circuit, the current is maximum when the impedance is equal to the resistance, thus, option (B) is correct.
Note: In the case of a capacitor, voltage lags current by \[90{}^\circ \]. In the case of an inductor, voltage leads current by \[90{}^\circ \]. Therefore, the voltages on the inductor and capacitor are \[180{}^\circ \]out of phase with each other so they have to be subtracted.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What is transplantation in agriculture class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Who discovered the cell and how class 12 biology CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?




