
In a meter bridge experiment, the null point is obtained at 20 cm from one end of the wire when resistance X is balanced against another resistance Y. If X is less than Y, then where will the new position of the null point be from the same end, if one decides to balance a resistance of 4X against Y?
A. 40 cm
B. 80 cm
C. 50 cm
D. 70 cm
Answer
584.1k+ views
Hint: Find the relation between X and Y with the formula $\dfrac{X}{Y}=\dfrac{l}{100-l}$, where l is balanced from X. Then with this relation, find the new balanced length when the resistance X is replaced with 4X.
Formula used:
$\dfrac{X}{Y}=\dfrac{l}{100-l}$
Complete step-by-step answer:
Let us first understand the application of a meter bridge. A meter bridge is a device to find the relation between two unknown resistances or to find the value of an unknown resistance with help of a known resistance. It works on the principle of Wheatstone bridge. The device has a wire, one meter long with uniform resistance and to slots to attach the two resistances. It has a jockey with one end attached to the junction of the two resistances. The other end is used to balance the bridge.
A diagram of a meter bridge is given below.
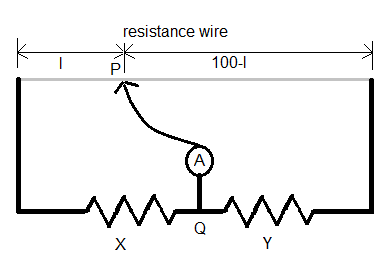
When the ammeter reads zero current, the bridge is balanced. We also call this a null point. Ats this point, the relation between the two resistances is given as:
$\dfrac{X}{Y}=\dfrac{l}{100-l}$, where X and Y are the values of the resistances.
Now, in the question, it is given that l=20cm.
Therefore, $\dfrac{X}{Y}=\dfrac{20}{100-20}=\dfrac{20}{80}=\dfrac{1}{4}$.
$\Rightarrow 4X=Y$.
The second case consists of resistances of 4X and Y. Let 4X=R and Y=S.
Hence, $\dfrac{R}{S}=\dfrac{l}{100-l}$
$\Rightarrow \dfrac{R}{S}=\dfrac{4X}{Y}=\dfrac{l}{100-l}$.
But we know that Y=4X.
Therefore,
$\dfrac{4X}{4X}=\dfrac{l}{100-l}$
$\Rightarrow 1=\dfrac{l}{100-l}$.
This implies that l=50 cm.
Therefore, when the resistance X is replaced with 4X, the new null point is obtained at a position of 50 cm from the end that has resistance 4X.
Hence, the correct option is C.
Note: The reason that we get a null point or zero current across P and Q is that the potential difference across P and Q is zero.
Please note that relation XY, then the position of the null point will also change. The smaller length is always in parallel with the resistance that has smaller value.
Formula used:
$\dfrac{X}{Y}=\dfrac{l}{100-l}$
Complete step-by-step answer:
Let us first understand the application of a meter bridge. A meter bridge is a device to find the relation between two unknown resistances or to find the value of an unknown resistance with help of a known resistance. It works on the principle of Wheatstone bridge. The device has a wire, one meter long with uniform resistance and to slots to attach the two resistances. It has a jockey with one end attached to the junction of the two resistances. The other end is used to balance the bridge.
A diagram of a meter bridge is given below.

When the ammeter reads zero current, the bridge is balanced. We also call this a null point. Ats this point, the relation between the two resistances is given as:
$\dfrac{X}{Y}=\dfrac{l}{100-l}$, where X and Y are the values of the resistances.
Now, in the question, it is given that l=20cm.
Therefore, $\dfrac{X}{Y}=\dfrac{20}{100-20}=\dfrac{20}{80}=\dfrac{1}{4}$.
$\Rightarrow 4X=Y$.
The second case consists of resistances of 4X and Y. Let 4X=R and Y=S.
Hence, $\dfrac{R}{S}=\dfrac{l}{100-l}$
$\Rightarrow \dfrac{R}{S}=\dfrac{4X}{Y}=\dfrac{l}{100-l}$.
But we know that Y=4X.
Therefore,
$\dfrac{4X}{4X}=\dfrac{l}{100-l}$
$\Rightarrow 1=\dfrac{l}{100-l}$.
This implies that l=50 cm.
Therefore, when the resistance X is replaced with 4X, the new null point is obtained at a position of 50 cm from the end that has resistance 4X.
Hence, the correct option is C.
Note: The reason that we get a null point or zero current across P and Q is that the potential difference across P and Q is zero.
Please note that relation X
Recently Updated Pages
Why is there a time difference of about 5 hours between class 10 social science CBSE

In cricket, what is a "pink ball" primarily used for?

In cricket, what is the "new ball" phase?

In cricket, what is a "death over"?

What is the "Powerplay" in T20 cricket?

In cricket, what is a "super over"?

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE




