Question

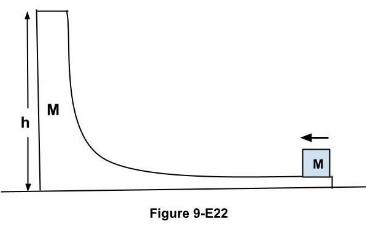
Figure (9-E22) shows a small body of mass m placed over a larger mass M whose surface is horizontal near the smaller mass and gradually curves to become vertical. The smaller mass is pushed on the longer one at a speed v and the system is left to itself. Assume that all the surfaces are frictionless.
(a) Find the speed of the larger block when the smaller block is sliding on the vertical part. (b) Find the speed of the smaller mass when it breaks off the larger mass at height $h$.
(c) Find the maximum height (from the ground) that the smaller mass ascends.
(d) Show that the smaller mass will again land on the bigger one. Find the distance traversed by the bigger block during the time when the smaller block was in its flight under gravity.

Answer 1

Hint:Friction is the force that keeps solid surfaces, fluid layers, and material elements moving in the same direction from colliding. Dry and wet friction are two types of friction. The relative lateral motion of two solid surfaces in contact is opposed by dry friction.

Complete step by step answer:

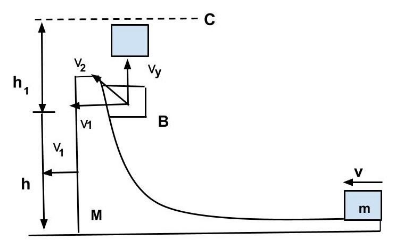
Over the bigger mass \[M\] , the mass is given a velocity.
(a) Allow the bigger block's velocity to be \[{v_1}\] towards the left when the smaller block is travelling vertically. Based on the conservation of momentum rule (in the horizontal direction).
$mv = \left( {M + m} \right){v_1} \\
\therefore {v_1} = \dfrac{{mv}}{{M + m}} $

(b) Let ${v_2}$ be the resultant velocity when the smaller block breaks apart.
From the law of conservation of energy
$\dfrac{1}{2}m{v^2} = \dfrac{1}{2}Mv_1^2 + \dfrac{1}{2}mv_2^2 + mgh \\
\Rightarrow v_2^2 = {v^2} - \dfrac{M}{m}v_1^2 - 2gh\,.....\left( 1 \right) \\
\Rightarrow v_2^2 = {v^2}\left[ {1 - \dfrac{M}{m} \times \dfrac{{{m^2}}}{{{{\left( {M + m} \right)}^2}}}} \right] - 2gh \\
\therefore {v_2} = {\left[ {\dfrac{{\left( {{m^2} + Mm + {m^2}} \right)}}{{{{\left( {M + m} \right)}^2}}}{v^2} - 2gh} \right]^{\dfrac{1}{2}}} $

(c) Now, the vertical component of the velocity ${v_2}$ of mass is given by;
$v_y^2 = v_2^2 - v_1^2 \\
= \dfrac{{\left( {{M^2} + Mm + {m^2}} \right)}}{{{{\left( {M + m} \right)}^2}}}{v^2} - 2gh - \dfrac{{{m^2}{v^2}}}{{{{\left( {M + m} \right)}^2}}} \\
\left[ {\because {v_1} = \dfrac{{M{v^2}}}{{\left( {M + v} \right)}}} \right] \\
\Rightarrow v_y^2 = \dfrac{{{M^2} + Mm + {m^2} - {m^2}}}{{{{\left( {M + m} \right)}^2}}}{v^2} - 2gh \\
\Rightarrow v_y^2 = \dfrac{{M{v^2}}}{{\left( {M + m} \right)}} - 2gh\,......\left( 2 \right) \\ $
To find the maximum height (from the ground), let us assume the body rises to a height , over and above .
Now, $\left( {\dfrac{1}{2}} \right)mv_y^2 = mg{h_1} \Rightarrow {h_1} = \dfrac{{v_y^2}}{{2g}}\,\,\,....\,\left( 3 \right)$
So, total height = $h + {h_1} = h + \dfrac{{v_y^2}}{{2g}} = h + \dfrac{{m{v^2}}}{{\left( {M + m} \right)2g}}$
[From equation (2) and (3)]
$\therefore H = \dfrac{{m{v^2}}}{{\left( {M + m} \right)2g}}$

(d) Because the smaller mass has also got a horizontal component of velocity at the time it breaks off from (which has a velocity ), the block ‘m’ will again land on the block (bigger one). Let us find out the time of flight of block ‘m’ after it breaks off. During the upward motion \[\left( {BC} \right)\]. Because the smaller mass has a horizontal component of velocity when it breaks away from (which also has a horizontal component of velocity ), the block will reappear on the block (bigger one). Let's calculate the time of flight of the block once it separates. During the ascension, \[BC\]
$0 = {v_y} - g{t_1} \\
\Rightarrow {t_1} = \dfrac{{{v_y}}}{g} = \dfrac{1}{g}{\left[ {\dfrac{{M{v^2}}}{{\left( {M + m} \right)}} - 2gh} \right]^{\dfrac{1}{2}}}......(4)\left[ {from\,equation\left( 2 \right)} \right] \\ $
So, the time for which the smaller block was in its flight is given by
$T = 2{t_1} \\
\Rightarrow T= \dfrac{2}{g}{\left[ {\dfrac{{M{v^2} - 2\left( {M + m} \right)gh}}{{\left( {M + m} \right)}}} \right]^{\dfrac{1}{2}}}$
So, the distance travelled by the bigger block during this time is;
$S = {v_1}T = \dfrac{{mv}}{{M + m}} \times \dfrac{2}{g}\dfrac{{{{\left[ {M{v^2} - 2\left( {M + m} \right)gh} \right]}^{\dfrac{1}{2}}}}}{{{{\left( {M + m} \right)}^{\dfrac{1}{2}}}}} \\
\therefore S = \dfrac{{2mv{{\left[ {M{v^2} - 2\left( {M + m} \right)gh} \right]}^{\dfrac{1}{2}}}}}{{g{{\left( {M + m} \right)}^{\dfrac{3}{{2M{v^2} - 2\left( {M + m} \right)gh}}}}}} $

Note:If the surface is frictionless, any force, no matter how great, will move it (provided that there is no opposing force from that direction). However, the acceleration will vary depending on the force. But in reality there is no such thing as frictionless, this is due to the fact that no matter how much we polish the surface, apply lubricants, and so on, there will always be a rough surface on a microscopic scale. Even ice has its own mui.