Question

How does kinetic energy and potential energy turn into each other and back again?

Answer 1

Hint: Usually, the potential energy and kinetic energy are expressed in terms of their height and velocity at the different positions and situations. So, by considering how an object is placed or is under movement, we can easily obtain the values of potential energy and kinetic energy and how the energy is turned into each other and back again.

Complete answer:
The conversion of kinetic and potential energy into each other and back to their forms can be explained by using the example of a simple pendulum.
Consider a simple pendulum as shown in the figure below.

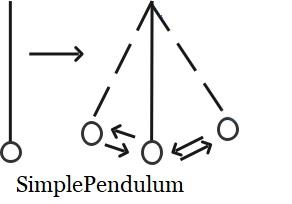
The formula for potential energy is
\[P.E.\text{ }=\text{ }m g h\]---(1)
Let this be equation (1)
Where,
m is the mass
g is the acceleration due to gravity
h is the height
The formula for kinetic energy is
\[K.E.\text{ }=\dfrac{1}{2}m{{v}^{2}}\]----(2)
Let this be equation (2)
Where,
v is the velocity
Initially, the pendulum is in the middle and not moving.
At this mean position, the pendulum is at its highest point of the swing.
At the highest point,
The height is maximum
But, the velocity doesn’t exist.
Therefore,
\[P.E.\text{ }=\text{ }m g h\]
But,
\[K.E.\text{ }=0\]
Therefore at the highest position,
Only the gravitational potential energy exists.
But, the kinetic energy does not exist.
Consider the pendulum is released next and it starts moving
Once it starts moving leftwards,
Kinetic energy increases and,
Potential energy starts decreasing
Then, it again comes back to its original position,
Where, the potential energy increases and kinetic energy decreases
Again, when it moves to the right,
Kinetic energy increases and potential energy decreases
Thus, the potential energy and kinetic energy are changed into each other and back again.

Note:
The total energy in a system always remains constant. So, when one energy increases, another form of energy decreases so that the energy in a system is balanced. Other examples of this may be the free fall of a body like an apple or a ball, the working of the spring, etc.