Question

Define electric capacity. Derive an expression for the capacitance of a parallel plate capacitor in which a dielectric medium of dielectric constant K fills the space between the plates. Draw the necessary diagram.

Answer 1

Hint: Consider two parallel plates of certain areas separated at a distance d much less as compared to that of the plate area each having an equal and opposite charge. Then find the electric field between the plates by considering the presence of a dielectric medium. Then using the electric field generated due to the opposite charges, find the potential difference and then ultimately, we will get the capacitance of the capacitor.

Complete step by step solution:
Electric capacity or the capacitance is the capacity of a system to store charges. For a conductor having a potential difference V across it, it stores a charge Q, then its electric capacity is given by, $C=\dfrac{Q}{V}$. The SI unit of capacitance is farad (F).
Parallel plate capacitor is the most commonly used capacitor. Let us consider a parallel plate capacitor consisting of two conducting plates A and B being $d$ distance apart which is very small as compared to the area of the plates. And due to very small separation, the fringing is negligible at the boundaries.

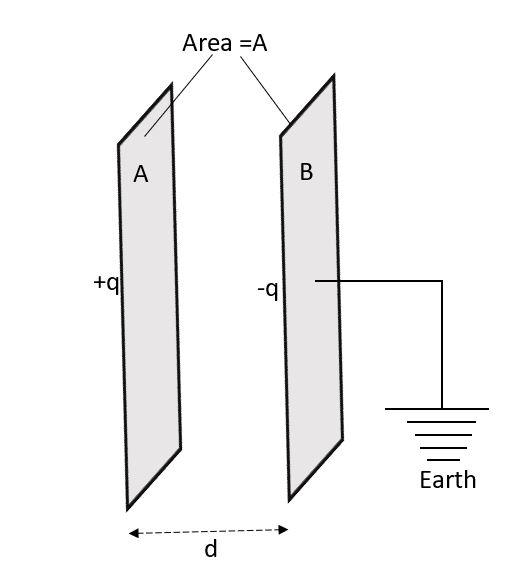
Now, if we give a charge +q to the plate A, then on plate B a charge -q will be induced on the left face of the plate B and charge -q on its right face. So, we will earthen plate B, the charge +q on its right face will flow to the earth and thus we will have +q charge on plate A and -q charge on plate B which will set up an electric field between the two plates.
Let the electric field be uniform and perpendicular to the plates. So, if the potential difference is given by V, then $E=\dfrac{V}{d}\; or\; V=Ed$ ………. (i)
Now, if $\sigma$ is the surface charge density of the plates, then the electric field between the plates will be $E=\dfrac{\sigma}{\varepsilon_0}$ ………. (ii)
where $\varepsilon$ is the absolute permittivity of the free space between the two plates as the medium has been considered as vacuum or air.
Substituting equation (ii) in equation (i), we get
$V=\dfrac{\sigma}{\varepsilon_0}d$
As, $\sigma =\dfrac{q}{A}$
Then, $V=\dfrac{qd}{\varepsilon_0 A}$ ………. (iii)
Now, if C is the capacitance of the capacitor, then
$C=\dfrac{q}{V}=\dfrac{q}{qd/\varepsilon_0 A}=\dfrac{\varepsilon_0 A}{d}$ ………. (iii)
Since, we have considered the medium between the two plates as vacuum or air, but according to the question a dielectric medium of dielectric constant K is present,
So, equation (ii) can be written as $E=\dfrac{q}{\varepsilon_0 KA}$
And equation (iii), will become $V=\dfrac{qd}{\varepsilon_0 KA}$
Thus, the capacitance will be $C=\dfrac{\varepsilon_0 KA}{d}$
This is the expression for the capacitance of a parallel plate capacitor in which a dielectric medium of dielectric constant K fills the space between the plates.

Note: We can also derive this directly by considering a dielectric medium instead of vacuum or air in the beginning. The earthing has been done so as to prevent accumulation of charge on the outside of the plates and generate unwanted electric fields.