
Define centripetal acceleration. Drive expression for centripetal acceleration of a particle moving with uniform speed v along a circular path of radius. Give the direction of the acceleration.
Answer
470.8k+ views
Hint: Centripetal acceleration occurs due to centripetal force. It is also called radial acceleration. Centripetal force tends to move a body in a circular path. It acts towards the centre of the body in which a body is traversing.
Complete step-by-step answer:
Centripetal Acceleration is the acceleration which acts towards the centre of the body. It is the property of a body. It is the property of a body performing circular motion.
It arises due to centripetal force which acts constantly towards the centre of the circle. It is perpendicular to the velocity. It is due to that change in velocity (in terms of direction such acceleration appears)
\[ac=\dfrac{\vartriangle V}{\vartriangle t}=\dfrac{{{V}^{2}}}{R}\]
V = velocity of particle
R = Radius
Suppose a body moving \[{{V}_{1}}\] with velocity transverses velocity changes to \[{{V}_{2}}\] .(In terms of direction) the net change in velocity generates the acceleration.
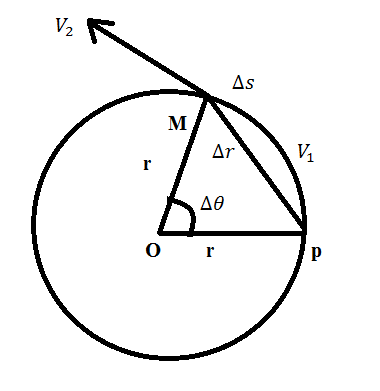
\[\vartriangle V={{V}_{2}}-{{V}_{1}}\]
\[\vartriangle s\to \]Change of radius of the length PM
\[\vartriangle r\to \]Displacement or arc length PM
As \[ac=\dfrac{\vartriangle V}{\vartriangle t}\] (the acceleration is towards center) \[\vartriangle Q\]as is small and \[\vartriangle s\approx \vartriangle r\]
.Now for magnitude,
The triangles PTR and OPM are similar above magnitude wise \[{{\text{V}}_{\text{1}}}\text{=}{{\text{V}}_{\text{2}}}\]so they form a 2 isosceles triangles.
So using property of similar triangles,
\[\frac{\vartriangle V}{V}=\dfrac{\vartriangle s}{r}\] …… 1
Centripetal acceleration is \[\dfrac{\vartriangle V}{\vartriangle t}\]
Multiply and divide by
\[\dfrac{\vartriangle \text{V}}{\vartriangle t}=\dfrac{\vartriangle s}{\vartriangle t}\frac{V}{r}\]
\[\dfrac{\vartriangle \text{V}}{\vartriangle t}=\] Acceleration (centripetal)
And that \[\dfrac{\vartriangle s}{\vartriangle t}=\] velocity (V) = linear / tangential velocity / speed
So
\[\text{ac=}\dfrac{{{\text{V}}^{\text{2}}}}{\text{R}}\] …. 2
So we have linear or that ac is perpendicular to linear or tangential velocity
Note:
Centrifugal force: It is the reaction centripetal force and acts away from the centre. Its magnitude is equal to that of centripetal force.
Complete step-by-step answer:
Centripetal Acceleration is the acceleration which acts towards the centre of the body. It is the property of a body. It is the property of a body performing circular motion.
It arises due to centripetal force which acts constantly towards the centre of the circle. It is perpendicular to the velocity. It is due to that change in velocity (in terms of direction such acceleration appears)
\[ac=\dfrac{\vartriangle V}{\vartriangle t}=\dfrac{{{V}^{2}}}{R}\]
V = velocity of particle
R = Radius
Suppose a body moving \[{{V}_{1}}\] with velocity transverses velocity changes to \[{{V}_{2}}\] .(In terms of direction) the net change in velocity generates the acceleration.

\[\vartriangle V={{V}_{2}}-{{V}_{1}}\]
\[\vartriangle s\to \]Change of radius of the length PM
\[\vartriangle r\to \]Displacement or arc length PM
As \[ac=\dfrac{\vartriangle V}{\vartriangle t}\] (the acceleration is towards center) \[\vartriangle Q\]as is small and \[\vartriangle s\approx \vartriangle r\]
.Now for magnitude,
The triangles PTR and OPM are similar above magnitude wise \[{{\text{V}}_{\text{1}}}\text{=}{{\text{V}}_{\text{2}}}\]so they form a 2 isosceles triangles.
So using property of similar triangles,
\[\frac{\vartriangle V}{V}=\dfrac{\vartriangle s}{r}\] …… 1
Centripetal acceleration is \[\dfrac{\vartriangle V}{\vartriangle t}\]
Multiply and divide by
\[\dfrac{\vartriangle \text{V}}{\vartriangle t}=\dfrac{\vartriangle s}{\vartriangle t}\frac{V}{r}\]
\[\dfrac{\vartriangle \text{V}}{\vartriangle t}=\] Acceleration (centripetal)
And that \[\dfrac{\vartriangle s}{\vartriangle t}=\] velocity (V) = linear / tangential velocity / speed
So
\[\text{ac=}\dfrac{{{\text{V}}^{\text{2}}}}{\text{R}}\] …. 2
So we have linear or that ac is perpendicular to linear or tangential velocity
Note:
Centrifugal force: It is the reaction centripetal force and acts away from the centre. Its magnitude is equal to that of centripetal force.
Recently Updated Pages
Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

What is the opposite of entropy class 11 chemistry CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




