Question

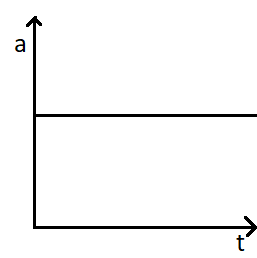
Corresponding to the acceleration time graph given below, draw x-t and v-t graphs.

Answer 1

Hint Since the acceleration is constant with time so the velocity is increasing at a constant rate. Thus from there we can draw the v-t graph. From the equation of motion we can see that the equation for position is quadratic in time so the graph will be parabolic.

Formula Used: In this solution we will be using the following formula,
 $\Rightarrow x = ut + \dfrac{1}{2}a{t^2} $
where $ x $ is the position, $ u $ is the initial velocity, $ a $ is the acceleration and $ t $ is the time.

Complete step by step answer
In the question we are given the graph of the acceleration with respect to time. In the graph we can see that it is a straight line which is parallel to the time axis. This means that the acceleration remains constant with time.
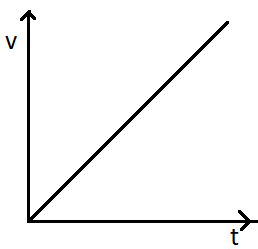
Now for a velocity time graph, the slope is given by $ \dfrac{{dv}}{{dt}} $ . Now the differentiation of velocity with respect to time gives us the acceleration. So we can write,
 $\Rightarrow \dfrac{{dv}}{{dt}} = a $
On integrating we get,
 $\Rightarrow v = u + at $
where the initial velocity can be taken as $ u = 0 $ for time 0. Hence we see that the velocity is directly proportional to the time. So the graph will be a straight line passing through the origin for $ u = 0 $ .
That is,

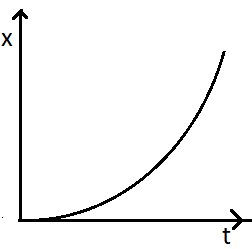
Now for the position time graph, again, the acceleration is the double differentiation of the position. So we can write,
 $\Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} = a $
On integrating twice we get,
 $\Rightarrow x = ut + \dfrac{1}{2}a{t^2} $
If the initial velocity is considered to be zero, for time zero, we get,
 $\Rightarrow x = \dfrac{1}{2}a{t^2} $
From here we can see that the position is a quadratic equation of time and represents the form of a parabola. So the graphical representation will be,

Note
Using the velocity time graph we can find both the acceleration and the displacement of the particle. The slope of the velocity time graph given the acceleration and the area covered under the velocity time graph gives the displacement of the particle.