
A wind powered generator converts wind energy into electrical energy. Assume that the generator converts a fixed fraction of the wind energy intercepted by its blades into electrical energy. For wind speed v, the electrical power output will be proportional to:
A. \[{\text{v}}\]
B. \[{{\text{v}}^2}\]
C. \[{{\text{v}}^3}\]
D. \[{{\text{v}}^4}\]
Answer
543.9k+ views
Hint: To comment on proportionality, we have to develop the expression of corresponding variable in terms of other for example in this question, to find the relation between power and velocity, we start with general formula of power i.e. is multiplication of force and velocity later on we used other definitions and formulas of Force, momentum, mass and equation of continuity to reach the final result.
Complete step-by-step answer:
Let’s us consider, \[{\text{v}}\]= wind speed
And we know that power is multiplication of force(F) and velocity(v)
Power, \[{\text{P = F}} \times {\text{v}}\] . . . . . . . . . . . . .(1)
We can write the force expression as rate of change of momentum(P) per unit time
Force, \[{\text{F}} = \dfrac{{d{\text{P}}}}{{dt}}\]
Momentum(P) is defined as multiplication of mass(m) and velocity(v)
\[{\text{F}} = \dfrac{{d{\text{P}}}}{{dt}} = \dfrac{{d\left( {{\text{m}}{\text{.v}}} \right)}}{{dt}}\]
On differentiation using $\dfrac{{du.v}}{{dt}} = u\dfrac{{dv}}{{dt}} + v\dfrac{{du}}{{dt}}$
\[ \Rightarrow {\text{F}} = {\text{m}}{\text{.}}\dfrac{{d\left( {\text{v}} \right)}}{{dt}} + {\text{v}}{\text{.}}\dfrac{{d\left( {\text{m}} \right)}}{{dt}}\]
And \[\dfrac{{d\left( {\text{v}} \right)}}{{dt}} = 0\] because it is given wind velocity v is constant hence its differentiation will be zero.
So, \[{\text{F}} = {\text{v}}{\text{.}}\dfrac{{d\left( {\text{m}} \right)}}{{dt}}\]
We can write mass is equal to density (ρ) multiplied by Volume(V) i.e. m = ρ.V
\[ \Rightarrow {\text{F}} = {\text{v}}{\text{.}}\dfrac{{d\left( \rho {\text{.V}} \right)}}{{dt}}\]
where, ρ= density of air which is constant so we can take it out from differentiation
V= volume
⇒F = v.ρ\[\dfrac{{d\left( {\text{V}} \right)}}{{dt}}\] ………..(2)
From the equation of continuity,
\[ \Rightarrow \dfrac{{d{\text{V}}}}{{dt}} = \] Area × velocity
This can be written as
\[ \Rightarrow \dfrac{{d{\text{V}}}}{{dt}} = {\text{A}}{\text{.v}}\]
On putting \[\dfrac{{d{\text{V}}}}{{dt}} = {\text{A}}{\text{.v}}\] in equation (2),
⇒F = v.ρ.A.v
On further solving
⇒F = ρ.A\[{{\text{v}}^2}\]
Substitute value of F in equation (1), we will get
⇒P= ρA\[{{\text{v}}^3}\]
Hence we can say
⇒ P ∝ \[{{\text{v}}^3}\]
Therefore, the correct option is C.
Note- In this particular question we should know that for incompressible fluids we can apply continuity equation.
Yes, air comes under a compressible fluid. But we can consider air as incompressible in duct systems because when pressure changes then there are no changes in density of the air which remain the same mathematically approx. 1.
The velocity of air in the smaller cross-section area is more where the area of cross-section is large.
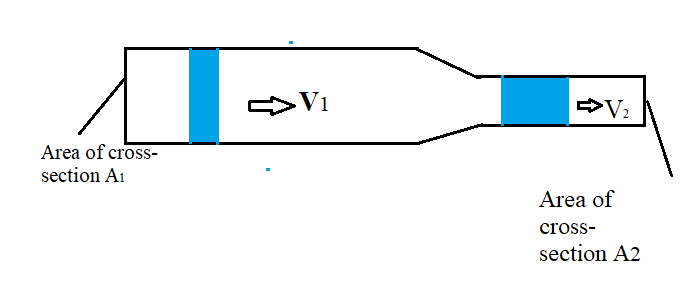
Hence multiplication of area and velocity remain constant at each and every point through the vessel or duct.
$ \Rightarrow {{\text{A}}_1} \times {{\text{V}}_1} = {{\text{A}}_2} \times {{\text{V}}_2}$
Complete step-by-step answer:
Let’s us consider, \[{\text{v}}\]= wind speed
And we know that power is multiplication of force(F) and velocity(v)
Power, \[{\text{P = F}} \times {\text{v}}\] . . . . . . . . . . . . .(1)
We can write the force expression as rate of change of momentum(P) per unit time
Force, \[{\text{F}} = \dfrac{{d{\text{P}}}}{{dt}}\]
Momentum(P) is defined as multiplication of mass(m) and velocity(v)
\[{\text{F}} = \dfrac{{d{\text{P}}}}{{dt}} = \dfrac{{d\left( {{\text{m}}{\text{.v}}} \right)}}{{dt}}\]
On differentiation using $\dfrac{{du.v}}{{dt}} = u\dfrac{{dv}}{{dt}} + v\dfrac{{du}}{{dt}}$
\[ \Rightarrow {\text{F}} = {\text{m}}{\text{.}}\dfrac{{d\left( {\text{v}} \right)}}{{dt}} + {\text{v}}{\text{.}}\dfrac{{d\left( {\text{m}} \right)}}{{dt}}\]
And \[\dfrac{{d\left( {\text{v}} \right)}}{{dt}} = 0\] because it is given wind velocity v is constant hence its differentiation will be zero.
So, \[{\text{F}} = {\text{v}}{\text{.}}\dfrac{{d\left( {\text{m}} \right)}}{{dt}}\]
We can write mass is equal to density (ρ) multiplied by Volume(V) i.e. m = ρ.V
\[ \Rightarrow {\text{F}} = {\text{v}}{\text{.}}\dfrac{{d\left( \rho {\text{.V}} \right)}}{{dt}}\]
where, ρ= density of air which is constant so we can take it out from differentiation
V= volume
⇒F = v.ρ\[\dfrac{{d\left( {\text{V}} \right)}}{{dt}}\] ………..(2)
From the equation of continuity,
\[ \Rightarrow \dfrac{{d{\text{V}}}}{{dt}} = \] Area × velocity
This can be written as
\[ \Rightarrow \dfrac{{d{\text{V}}}}{{dt}} = {\text{A}}{\text{.v}}\]
On putting \[\dfrac{{d{\text{V}}}}{{dt}} = {\text{A}}{\text{.v}}\] in equation (2),
⇒F = v.ρ.A.v
On further solving
⇒F = ρ.A\[{{\text{v}}^2}\]
Substitute value of F in equation (1), we will get
⇒P= ρA\[{{\text{v}}^3}\]
Hence we can say
⇒ P ∝ \[{{\text{v}}^3}\]
Therefore, the correct option is C.
Note- In this particular question we should know that for incompressible fluids we can apply continuity equation.
Yes, air comes under a compressible fluid. But we can consider air as incompressible in duct systems because when pressure changes then there are no changes in density of the air which remain the same mathematically approx. 1.
The velocity of air in the smaller cross-section area is more where the area of cross-section is large.

Hence multiplication of area and velocity remain constant at each and every point through the vessel or duct.
$ \Rightarrow {{\text{A}}_1} \times {{\text{V}}_1} = {{\text{A}}_2} \times {{\text{V}}_2}$
Recently Updated Pages
JEE Main 2025-26 Mock Test: Matrices and Determinants

JEE Main 2025-26 Mock Test: Complex Numbers & Quadratic Equations

NCERT Solutions For Class 12 Maths Three Dimensional Geometry Exercise 11.2

NCERT Solutions For Class 11 Maths Sets Exercise 1.4

NCERT Solutions For Class 11 Maths Miscellaneous Exercise - Limits and Derivatives

NCERT Solutions For Class 12 Maths Integrals Exercise 7.9

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE




