Question

A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. Find the ratio of the volume of the smaller cone to the whole cone.

Answer 1

Hint: Here we need to find the ratio of the volume of the smaller cone that has been obtained by cutting the whole cone at the middle of its height parallel to its bast to the volume of the whole cone. Since we don’t have any particular value for this problem we will take the general form of the volume of the cone. then for the smaller cone the height will be half of the height of the whole cone using this we fill find the required ratio.

Complete answer:
Let the radius and the height of the whole solid right circular cone be \[r\] and \[h\] respectively.
By drawing a plane through the midpoint of its height the cone is divided into two parts such that the bases of both the cones are parallel.
Thus, the height of the smaller cone will become \[h/2\] .

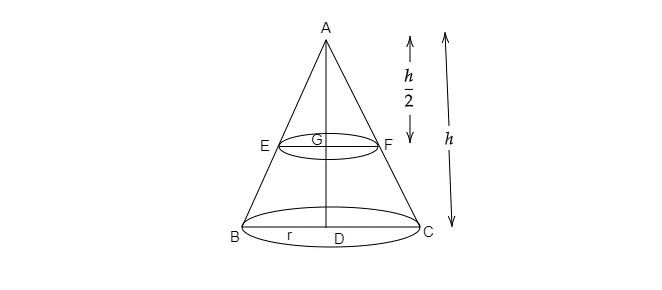
\[AD = h\]
\[DC = r\]
Since we cut the right circular cone into two parts at the middle of its height by a plane parallel to its base so its height becomes,
\[\therefore AG = h/2\]

In ∆AGF and ∆ADC, we have
\[1)\;\;\;\;\angle AFG{\text{ }} = \angle ACD\;\]
\[2)\;\;\;\;\because EF||BC\]
\[ \angle AGF = \angle ADC\left( {90^\circ } \right)\]
According to AA similarity, we conclude that
\[\therefore \vartriangle AGF \sim \vartriangle ADC\]
To find the radius of a smaller cone :
Since we have two similar right angle triangle
\[\because \vartriangle AGF \sim \vartriangle ADC\]
Let,
\[ \angle DAC = \angle GEF = \theta \]
\[\tan \theta = \dfrac{{GF}}{{AG}} = \dfrac{{DC}}{{AD}}\]
\[ \Rightarrow \] \[\dfrac{{GF}}{{DC}} = \dfrac{{AG}}{{AD}}\]
Now placing values,
\[ \Rightarrow \] \[\dfrac{{GF}}{{DC}} = \dfrac{{h/2}}{h}\]
\[\therefore \dfrac{{GF}}{{DC}} = \dfrac{1}{2}\]
\[\therefore \dfrac{{GF}}{r} = \dfrac{1}{2}\]
\[GF = \dfrac{r}{2}\]
Thus, we have found the radius of the small cone as \[GF = \dfrac{r}{2}\]
Now, we have the height and radius of both the smaller cone and the whole cone.
To find the requird ratio we have to find:
\[\dfrac{{Volume{\text{ }}of{\text{ }}smaller{\text{ }}cone}}{{Volume{\text{ }}of{\text{ }}whole{\text{ }}cone}}\]
\[ = \dfrac{{1/3\pi (GF){}^2AG}}{{1/3\pi {{(DC)}^2}AD}}\]
\[ = \dfrac{{1/3\pi (r/2){}^2(h/2)}}{{1/3\pi {r^2}h}}\]
\[ = \dfrac{{r{}^2h/8}}{{{r^2}h}}\]
\[ = \dfrac{1}{8}\]
So, the ratio of the volume of the smaller cone to the volume of the whole solid right circular cone is \[1:8\]

Note:
Similar triangles are the same shape, but not necessarily the same size considering this, apply triangle properties carefully. When finding the ratio keep in mind that in the question it is asked for a smaller cone to the whole cone. So the first term of the ratio should belong to the smaller cone and the next term of the ratio should belong to the whole cone.