
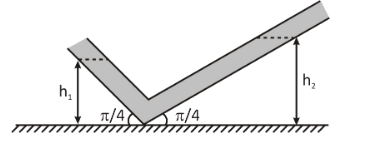
A simple accelerometer (an instrument for measuring acceleration) can be made in the form of a tube with a liquid and bent as shown. During motion, the level of the liquid in the left arm will be at height \[{h_1}\] and in the right arm at a height \[{h_2}\] . Determine the acceleration of a carriage in which the accelerometer was installed, assuming that the diameter of the tube is much smaller than \[{h_1}\] and \[{h_2}\] .
A. \[\dfrac{{g\left( {{h_1} - {h_2}} \right)}}{{{h_1} + {h_2}}}\]
B. \[\dfrac{{g\left( {{h_1} + {h_2}} \right)}}{{{h_1} - {h_2}}}\]
C. \[\dfrac{{g\left( {{h_2} - {h_1}} \right)}}{{{h_1} + {h_2}}}\]
D. \[\dfrac{{g\left( {{h_2}} \right)}}{{{h_2} - {h_1}}}\]

Answer
556.8k+ views
Hint:First of all, we will draw the diagram in detail and will mark all the dimensions in it, as per required by the question. We will find the expression for the pressure difference between the two points while the carriage is moving. After that we will again find the expression for the pressure difference due to gravity. We will equate the both.
Complete step by step answer:
In the given question, we are supplied with the following information:
There is an accelerometer, which is installed on a horizontal plane, with two arms in the shape of a tube.Both the arms are inclined at an angle of \[\dfrac{\pi }{4}\] , with the horizontal plane.During the motion of the carriage, on which it was installed, the level of the liquid in the left arm will be at height \[{h_1}\] and in the right arm at a height \[{h_2}\] .
It is directed to assume that the diameter of the tube is much smaller than \[{h_1}\] and \[{h_2}\] .We are asked to find the acceleration of the carriage.
To begin with, we will draw a diagram to understand the situation much better, as shown below.
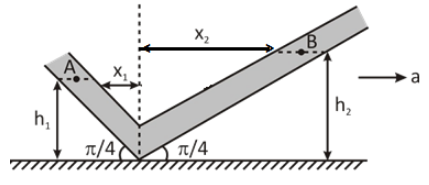
Let us assume the individual pressure of the liquid at the points \[{\text{A}}\] and \[{\text{B}}\] be \[{P_{\text{A}}}\] and \[{P_{\text{B}}}\] respectively.
The acceleration of the tube which is moving along with the carriage be \[a\] . The horizontal distance between the two points \[{\text{A}}\] and \[{\text{B}}\] be \[l\] .
So, we will now find the difference in pressure of the liquid between these two points, as given below:
\[{P_{\text{B}}} - {P_{\text{A}}} = \rho al\] …… (1)
Where,
\[\rho \] indicates the density of the liquid.
\[a\] indicates the acceleration of the tube.
\[l\] indicates the horizontal distance between the two points \[{\text{A}}\] and \[{\text{B}}\].
Again, we have
\[l = {x_1} + {x_2}\]
\[\therefore {P_{\text{B}}} - {P_{\text{A}}} = \rho a\left( {{x_1} + {x_2}} \right)\] …… (2)
Now, we use trigonometry in the triangle at the left side.
\[
\tan \dfrac{\pi }{4} = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}} \\
\Rightarrow 1 = \dfrac{{{x_1}}}{{{h_1}}} \\
\Rightarrow {x_1} = {h_1} \\
\]
Similarly, we can also apply trigonometry in the triangle at the right side and show that:
\[{x_2} = {h_2}\]
Now, we can write the equation (2) as:
\[{P_{\text{B}}} - {P_{\text{A}}} = \rho a\left( {{h_1} + {h_2}} \right)\] …… (3)
Again, we know that the pressure difference between those two points, due to gravity is written as:
\[{P_{\text{B}}} - {P_{\text{A}}} = \rho g\left( {{h_2} - {h_1}} \right)\] …… (4)
The two differences in pressure just found above will exactly be equal. So, we can compare the equations (3) and (4):
\[
\rho a\left( {{h_1} + {h_2}} \right) = \rho g\left( {{h_2} - {h_1}} \right) \\
\Rightarrow a\left( {{h_1} + {h_2}} \right) = g\left( {{h_2} - {h_1}} \right) \\
\therefore a = \dfrac{{g\left( {{h_2} - {h_1}} \right)}}{{{h_1} + {h_2}}} \\
\]
Hence, the acceleration of the carriage is \[\dfrac{{g\left( {{h_2} - {h_1}} \right)}}{{{h_1} + {h_2}}}\] .
Note: While solving this problem, most of the students tend to make mistakes while finding the correct expression of pressure when the carriage is moving. This pressure is a function of the horizontal distance between the two points. It is important to remember that the pressure due to gravity is a function of the height of the two points.
Complete step by step answer:
In the given question, we are supplied with the following information:
There is an accelerometer, which is installed on a horizontal plane, with two arms in the shape of a tube.Both the arms are inclined at an angle of \[\dfrac{\pi }{4}\] , with the horizontal plane.During the motion of the carriage, on which it was installed, the level of the liquid in the left arm will be at height \[{h_1}\] and in the right arm at a height \[{h_2}\] .
It is directed to assume that the diameter of the tube is much smaller than \[{h_1}\] and \[{h_2}\] .We are asked to find the acceleration of the carriage.
To begin with, we will draw a diagram to understand the situation much better, as shown below.

Let us assume the individual pressure of the liquid at the points \[{\text{A}}\] and \[{\text{B}}\] be \[{P_{\text{A}}}\] and \[{P_{\text{B}}}\] respectively.
The acceleration of the tube which is moving along with the carriage be \[a\] . The horizontal distance between the two points \[{\text{A}}\] and \[{\text{B}}\] be \[l\] .
So, we will now find the difference in pressure of the liquid between these two points, as given below:
\[{P_{\text{B}}} - {P_{\text{A}}} = \rho al\] …… (1)
Where,
\[\rho \] indicates the density of the liquid.
\[a\] indicates the acceleration of the tube.
\[l\] indicates the horizontal distance between the two points \[{\text{A}}\] and \[{\text{B}}\].
Again, we have
\[l = {x_1} + {x_2}\]
\[\therefore {P_{\text{B}}} - {P_{\text{A}}} = \rho a\left( {{x_1} + {x_2}} \right)\] …… (2)
Now, we use trigonometry in the triangle at the left side.
\[
\tan \dfrac{\pi }{4} = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}} \\
\Rightarrow 1 = \dfrac{{{x_1}}}{{{h_1}}} \\
\Rightarrow {x_1} = {h_1} \\
\]
Similarly, we can also apply trigonometry in the triangle at the right side and show that:
\[{x_2} = {h_2}\]
Now, we can write the equation (2) as:
\[{P_{\text{B}}} - {P_{\text{A}}} = \rho a\left( {{h_1} + {h_2}} \right)\] …… (3)
Again, we know that the pressure difference between those two points, due to gravity is written as:
\[{P_{\text{B}}} - {P_{\text{A}}} = \rho g\left( {{h_2} - {h_1}} \right)\] …… (4)
The two differences in pressure just found above will exactly be equal. So, we can compare the equations (3) and (4):
\[
\rho a\left( {{h_1} + {h_2}} \right) = \rho g\left( {{h_2} - {h_1}} \right) \\
\Rightarrow a\left( {{h_1} + {h_2}} \right) = g\left( {{h_2} - {h_1}} \right) \\
\therefore a = \dfrac{{g\left( {{h_2} - {h_1}} \right)}}{{{h_1} + {h_2}}} \\
\]
Hence, the acceleration of the carriage is \[\dfrac{{g\left( {{h_2} - {h_1}} \right)}}{{{h_1} + {h_2}}}\] .
Note: While solving this problem, most of the students tend to make mistakes while finding the correct expression of pressure when the carriage is moving. This pressure is a function of the horizontal distance between the two points. It is important to remember that the pressure due to gravity is a function of the height of the two points.
Recently Updated Pages
Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

The camels hump is made of which tissues a Skeletal class 11 biology CBSE




