Question

What is a rigid body? State and explain parallel and perpendicular axes theorem of moment of inertia.

Answer 1

Hint: Rigid body that does not deform or change shape.The parallel axes theorem as moment of inertia a body about any axis is equal to momentum sum of moment of inertia around ceret of gravity and mass multiply by distance between two parallel line whereas in perpendicular axes theorem sum of momentum inertia of two axes equal to the moment of inertia of third axes.

Complete step by step answer:
Rigid body:
It is a property of the body which is not deformed under the action of external force or we can also say that two given points of a rigid body remain constant in time regardless of external forces exerted on it. It is also defined as a collection of particles with the property that the distance between particles remains unchanged during the course of motion of the body.
Metal rod is an example of a rigid body.
Parallel Axes Theorem:
According to the parallel axis theorem, the moment of inertia of a given body about any axis through the center of gravity and the product of the mass of the body and the square of the distance between the two axes. It is used to determine the moment of inertia or the second moment of area of a rigid body about any axis.
Explanation:
Let us first draw a rough diagram to explain parallel axis theorem

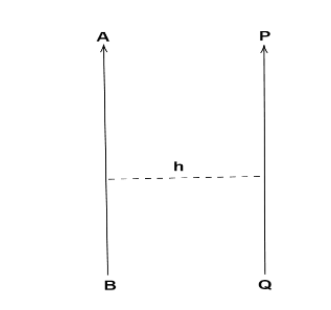
From this diagram we can define that the moment of inertia of a rigid body about an axis AB is equal to the moment of inertia about axis PQ passing through the center of mass of the body in a direct parallel to AB added with the product of mass of the body and square of the perpendicular distance h between the two parallel axis.
Let I_C be the moment of inertia of a body of mass M about an axis PQ which passes through the center of gravity.
According to the statement we can find the moment of inertia of a body about AB axis.
Now we can write,
$I = IC + M{h^2}$

Perpendicular Axes Theorem:
According to this theorem the moment of inertia of a two dimensional body of any shape about any axes is perpendicular to the two dimensional body is the total of the moment of inertia of the body about any two mutually perpendicular axis OX and OY in the plane of the body meeting in point where OZ axis passes through the body.

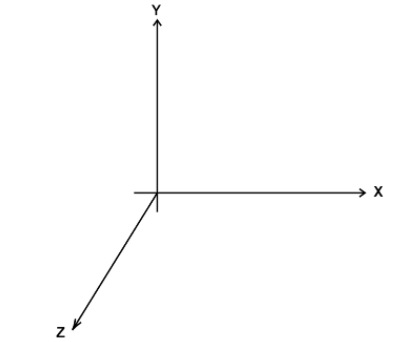
Explanation:
 $IX = $ Moment of inertia of the body about OX axis
$IY = $ Moment of inertia of the body about OY axis
$IZ = $ Moment of inertia of the body about OZ axis

According to the perpendicular axes theorem we can write:
$IX + IY = IZ$

Note:
This theorem helps to find the moment of inertia of a body in a simple way with less number of steps. According to the diagram only we can write the formula for the perpendicular axis theorem. We can also write $IZ + IY = IX$ using the perpendicular axis statement.