
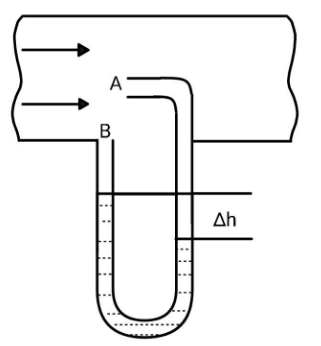
A Pitot tube (shown in figure) is mounted along the axis of a gas pipeline whose cross-sectional area is equal to $S$. Assuming the viscosity to be negligible, the volume of gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to $\Delta h$ and the densities of the liquid and the gas are \[{\rho _0}\] and \[\rho \] respectively.

Answer
495.9k+ views
Hint: Here, we are supposed to find the rate of flow of gas along the pipeline. As we are given a flow of gas, we can apply Bernoulli's theorem at point A and point B. The volume of gas flowing across the section of the pipe per unit time can be found out in terms of cross section area and the velocity of the gas.
Complete step by step answer:
The gas will flow along the pipeline, but as it reaches point B, it will flow over the tube and then continue with its path. As it reaches point A, it will enter the pipe and the remaining part other than the liquid will be occupied by the gas. Now, the gas that will reach point A, will stop as the tube already contains the gas. Hence, we conclude, that the velocity of the gas at point A will be zero. The height difference occurring is due to the pressure difference between point A and point B. Let the velocity of the gas be $v$. Applying Bernoulli’s equation, we get,
$
{P_A} + \dfrac{1}{2}\rho {\left( 0 \right)^2} = {P_B} + \dfrac{1}{2}\rho {v^2} \\
\Rightarrow {P_A} - {P_B} = \dfrac{1}{2}\rho {v^2} \\ $
This pressure difference has to be equal to ${\rho _0}g\Delta h$. Therefore, we have,
$\dfrac{1}{2}\rho {v^2} = {\rho _0}g\Delta h \\
\Rightarrow v = \sqrt {\dfrac{{2g\Delta h{\rho _0}}}{\rho }} $
We got the velocity of the gas. Now, if we will multiply the velocity with the cross-sectional area of the pipeline, we will get the volume rate flow.
Therefore, the volume of gas flowing across the section of the pipe per unit time will be $S\sqrt {\dfrac{{2g\Delta h{\rho _0}}}{\rho }} $.
Note: Remember that whenever a flow of gas or liquid is given between any two points, the first thing you should think of should be Bernoulli’s theorem and also remember Bernoulli's theorem. Also keep in mind the value of pressure difference that occurs due to height difference in the level of liquids.
Complete step by step answer:
The gas will flow along the pipeline, but as it reaches point B, it will flow over the tube and then continue with its path. As it reaches point A, it will enter the pipe and the remaining part other than the liquid will be occupied by the gas. Now, the gas that will reach point A, will stop as the tube already contains the gas. Hence, we conclude, that the velocity of the gas at point A will be zero. The height difference occurring is due to the pressure difference between point A and point B. Let the velocity of the gas be $v$. Applying Bernoulli’s equation, we get,
$
{P_A} + \dfrac{1}{2}\rho {\left( 0 \right)^2} = {P_B} + \dfrac{1}{2}\rho {v^2} \\
\Rightarrow {P_A} - {P_B} = \dfrac{1}{2}\rho {v^2} \\ $
This pressure difference has to be equal to ${\rho _0}g\Delta h$. Therefore, we have,
$\dfrac{1}{2}\rho {v^2} = {\rho _0}g\Delta h \\
\Rightarrow v = \sqrt {\dfrac{{2g\Delta h{\rho _0}}}{\rho }} $
We got the velocity of the gas. Now, if we will multiply the velocity with the cross-sectional area of the pipeline, we will get the volume rate flow.
Therefore, the volume of gas flowing across the section of the pipe per unit time will be $S\sqrt {\dfrac{{2g\Delta h{\rho _0}}}{\rho }} $.
Note: Remember that whenever a flow of gas or liquid is given between any two points, the first thing you should think of should be Bernoulli’s theorem and also remember Bernoulli's theorem. Also keep in mind the value of pressure difference that occurs due to height difference in the level of liquids.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

At which age domestication of animals started A Neolithic class 11 social science CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




