
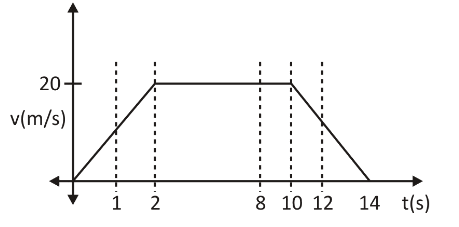
A person of mass M standing on a lift. The lift is moving upwards according to given V-t graph then find out the weight of man at the following instant
(I) \[t=1\] second
(II) \[t=8\] second
(III) \[t=10,12\] and 14 second

Answer
482.7k+ views
Hint: Human weight is just the normal reaction force that earth applies to us so. The slope of the Velocity vs time graph gives the resultant acceleration of the lift. After finding the acceleration of the lift we can apply Newton law of motion to find the normal reaction force.
Complete step by step solution:
Given: \[g=10m{{s}^{-2}}\]
(I) weight at instant \[t=1\] second
slope ${m_1}$ of given graph from \[t=0\] to \[t=2\] second is given as
\[{{m}_{1}}=\dfrac{20}{2}=10\]
This value of slope is equal to acceleration of the lift from \[t=0\] to \[t=2\] second then apply newton law lift has upward acceleration of \[10m/{{s}^{2}}\]
\[
N-Mg=M\times 10 \\
\Rightarrow N=M\left( 10+g \right) \\
\Rightarrow N=M\text{ }\left( 10+10 \right) \\
\]
\[\mathbf{N}=\mathbf{20M}\] newton at \[t=1\] seconds.
(II) weight at instant \[t=8\] second
slope (\[{{m}_{2}}\]) of given graph from \[t=2\]to \[t=10\] second is given as \[{{m}_{2}}\text{ =}\dfrac{0}{8}=0\]
slope is zero so lift acceleration during \[t=2\]to \[t=10\] second is zero
then applying newton's law
\[
N-Mg=M\times 0 \\
\Rightarrow N=Mg \\
\]
\[\mathbf{N}=\mathbf{10M}\text{ }\] newton at \[t=8\] second.
(III) weight at instant \[t=10,12,14\]second
slope (\[{{m}_{3}}\]) of given graph from \[t=10\] to \[t=14\] second is given as
\[{{m}_{3}}=\dfrac{-20}{4}=-5m/{{s}^{2}}\]
This time the acceleration is negative means in downward direction applying Newton's law of motion.
\[
Mg-N=M\times 5 \\
\Rightarrow N=10M-5M \\
\]
\[\mathbf{N}=\mathbf{5M}\]newton at \[t=10,12,14\] second.
Note:While solving this problem, most of the students tend to make mistakes in finding the slope of the curve at various instants. It should be remembered that when the lift is accelerating upwards the weight acting downward increases. This is because the floor of the lift presses harder to our feet while ascending upwards. When the lift moves with constant velocity, the net acceleration of the lift is zero, as we know acceleration is nothing but rate of change of velocity.
Complete step by step solution:
Given: \[g=10m{{s}^{-2}}\]
(I) weight at instant \[t=1\] second
slope ${m_1}$ of given graph from \[t=0\] to \[t=2\] second is given as
\[{{m}_{1}}=\dfrac{20}{2}=10\]
This value of slope is equal to acceleration of the lift from \[t=0\] to \[t=2\] second then apply newton law lift has upward acceleration of \[10m/{{s}^{2}}\]
\[
N-Mg=M\times 10 \\
\Rightarrow N=M\left( 10+g \right) \\
\Rightarrow N=M\text{ }\left( 10+10 \right) \\
\]
\[\mathbf{N}=\mathbf{20M}\] newton at \[t=1\] seconds.
(II) weight at instant \[t=8\] second
slope (\[{{m}_{2}}\]) of given graph from \[t=2\]to \[t=10\] second is given as \[{{m}_{2}}\text{ =}\dfrac{0}{8}=0\]
slope is zero so lift acceleration during \[t=2\]to \[t=10\] second is zero
then applying newton's law
\[
N-Mg=M\times 0 \\
\Rightarrow N=Mg \\
\]
\[\mathbf{N}=\mathbf{10M}\text{ }\] newton at \[t=8\] second.
(III) weight at instant \[t=10,12,14\]second
slope (\[{{m}_{3}}\]) of given graph from \[t=10\] to \[t=14\] second is given as
\[{{m}_{3}}=\dfrac{-20}{4}=-5m/{{s}^{2}}\]
This time the acceleration is negative means in downward direction applying Newton's law of motion.
\[
Mg-N=M\times 5 \\
\Rightarrow N=10M-5M \\
\]
\[\mathbf{N}=\mathbf{5M}\]newton at \[t=10,12,14\] second.
Note:While solving this problem, most of the students tend to make mistakes in finding the slope of the curve at various instants. It should be remembered that when the lift is accelerating upwards the weight acting downward increases. This is because the floor of the lift presses harder to our feet while ascending upwards. When the lift moves with constant velocity, the net acceleration of the lift is zero, as we know acceleration is nothing but rate of change of velocity.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




