
A cylinder boiler 4 m high and 3.5 m in diameter has a hemispherical lid. Find the volume of the boiler including the part covered by the lid?
Answer
538.8k+ views
Hint: To know the volume of the boiler along with the lid we are going to add the volume of cylinder with volume of hemisphere. We know that the volume of the cylinder is equal to $\pi {{r}^{2}}h$ with r and h as radius and height of the cylinder. We also know that the volume of the hemisphere is equal to $\dfrac{2}{3}\pi {{r}^{3}}$ where r is the radius of the hemisphere. The necessary dimensions to be substituted in the equation are given in the question, draw the figure and get those. Then we can easily find the volume of the boiler.
Complete step-by-step answer:
It is given that the cylindrical boiler is 4 m high and 3.5 m in diameter. The radius of the cylindrical boiler is calculated by dividing the diameter by 2.
$r=\dfrac{3.5}{2}=1.75m$
In the below figure we have drawn a cylinder with radius r and height h.
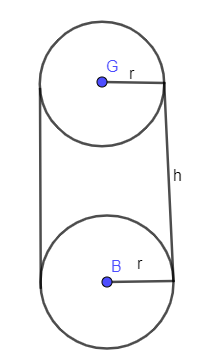
We know that volume of the cylinder is equal to:
$\pi {{r}^{2}}h$
Substituting the value of r as 1.75 m, height as 4 m and $\pi =\dfrac{22}{7}$ in the above equation we get,
$\begin{align}
& \dfrac{22}{7}{{\left( 1.75 \right)}^{2}}\left( 4 \right) \\
& =\dfrac{269.5}{7} \\
& =38.5{{m}^{3}} \\
\end{align}$
In the below diagram we have drawn the cylindrical boiler with a hemispherical lid.
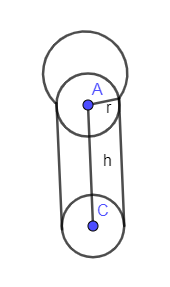
In the above diagram, a hemispherical lid is shown with a radius of 1.75 m. We have taken the radius the same as the cylindrical boiler. The total volume of this figure is the addition of the cylinder and the hemisphere. We have already shown the volume of the cylinder above.
Volume of hemisphere is equal to:
$\dfrac{2}{3}\pi {{r}^{3}}$
Substituting the value of r as 1.75 m in the above expression we get,
$\begin{align}
& \dfrac{2}{3}\left( \dfrac{22}{7} \right){{\left( 1.75 \right)}^{3}} \\
& =\dfrac{44\left( 1.75 \right){{\left( 1.75 \right)}^{2}}}{3\left( 7 \right)} \\
\end{align}$
Dividing 1.75 by 7 we get 0.25 so substituting this value in the above expression we get,
$\begin{align}
& =\dfrac{44{{\left( 1.75 \right)}^{2}}\left( .25 \right)}{3} \\
& =11.23{{m}^{3}} \\
\end{align}$
Adding the volume of cylinder and hemisphere by taking its value from the above solution we get,
$\begin{align}
& \left( 38.5+11.23 \right){{m}^{3}} \\
& =49.73{{m}^{3}} \\
\end{align}$
Hence, the volume of the boiler including the part covered by the lid is $49.73{{m}^{3}}$.
Note: In this problem, as radius of the hemisphere is not given so you might think what radius we should take so the answer is when you put a lid on the vessel while cooking you have seen that the diameter of the lid and vessel is the same. Similarly, the diameter of the cylindrical boiler and the hemispherical lid is the same.
One more thing which is quite observed is that usually students write the volume of hemisphere as $\dfrac{4}{3}\pi {{r}^{3}}$ which is the volume of sphere so try to avoid making such mistake.
Complete step-by-step answer:
It is given that the cylindrical boiler is 4 m high and 3.5 m in diameter. The radius of the cylindrical boiler is calculated by dividing the diameter by 2.
$r=\dfrac{3.5}{2}=1.75m$
In the below figure we have drawn a cylinder with radius r and height h.

We know that volume of the cylinder is equal to:
$\pi {{r}^{2}}h$
Substituting the value of r as 1.75 m, height as 4 m and $\pi =\dfrac{22}{7}$ in the above equation we get,
$\begin{align}
& \dfrac{22}{7}{{\left( 1.75 \right)}^{2}}\left( 4 \right) \\
& =\dfrac{269.5}{7} \\
& =38.5{{m}^{3}} \\
\end{align}$
In the below diagram we have drawn the cylindrical boiler with a hemispherical lid.

In the above diagram, a hemispherical lid is shown with a radius of 1.75 m. We have taken the radius the same as the cylindrical boiler. The total volume of this figure is the addition of the cylinder and the hemisphere. We have already shown the volume of the cylinder above.
Volume of hemisphere is equal to:
$\dfrac{2}{3}\pi {{r}^{3}}$
Substituting the value of r as 1.75 m in the above expression we get,
$\begin{align}
& \dfrac{2}{3}\left( \dfrac{22}{7} \right){{\left( 1.75 \right)}^{3}} \\
& =\dfrac{44\left( 1.75 \right){{\left( 1.75 \right)}^{2}}}{3\left( 7 \right)} \\
\end{align}$
Dividing 1.75 by 7 we get 0.25 so substituting this value in the above expression we get,
$\begin{align}
& =\dfrac{44{{\left( 1.75 \right)}^{2}}\left( .25 \right)}{3} \\
& =11.23{{m}^{3}} \\
\end{align}$
Adding the volume of cylinder and hemisphere by taking its value from the above solution we get,
$\begin{align}
& \left( 38.5+11.23 \right){{m}^{3}} \\
& =49.73{{m}^{3}} \\
\end{align}$
Hence, the volume of the boiler including the part covered by the lid is $49.73{{m}^{3}}$.
Note: In this problem, as radius of the hemisphere is not given so you might think what radius we should take so the answer is when you put a lid on the vessel while cooking you have seen that the diameter of the lid and vessel is the same. Similarly, the diameter of the cylindrical boiler and the hemispherical lid is the same.
One more thing which is quite observed is that usually students write the volume of hemisphere as $\dfrac{4}{3}\pi {{r}^{3}}$ which is the volume of sphere so try to avoid making such mistake.
Recently Updated Pages
Physics and Measurement Mock Test 2025 – Practice Questions & Answers

NCERT Solutions For Class 5 English Marigold - The Little Bully

NCERT Solutions For Class 12 Maths Three Dimensional Geometry Exercise 11.1

NCERT Solutions For Class 11 English Woven Words (Poem) - Ajamil And The Tigers

NCERT Solutions For Class 6 Hindi Durva - Bhaaloo

NCERT Solutions For Class 12 Physics In Hindi - Wave Optics

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




