
A carnot engine working between $300K$ and $600K$ has work output of $800J$ per cycle. The amount of heat energy supplied to the engine from source per cycle will be:
A) $1000J$
B) $1600J$
C) $1200J$
D) $900J$
Answer
521.7k+ views
Hint:
To solve this question we have use formula of efficiency of carnot engine which is given by $\eta $
$\eta = \dfrac{w}{{{Q_1}}} = \dfrac{{{Q_1} - {Q_2}}}{{{Q_1}}} = \dfrac{{{T_1} - {T_2}}}{{{T_1}}}$
Where $w \Rightarrow $ work done by substance
${Q_1} \Rightarrow $ Heat taken from source
${Q_2} \Rightarrow $ Remaining heat given to sink
${T_1} \Rightarrow $ Temperature of source
${T_2} \Rightarrow $ Temperature of sink
Step by step solution:
Step 1
In a carnot engine substance take heat or energy from a source which is at temperature ${T_1}$ and change some amount of heat into work $w$ and remaining heat transfer to sink at temperature ${T_2}$ as shown in the diagram.
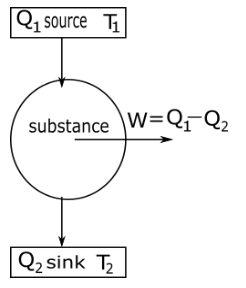
Efficiency of Carnot engine $\eta $ defined as the ratio of net work done $w$ by the engine during one cycle to the heat taken in from the source ${Q_1}$ in one cycle thus.
$ \Rightarrow \eta = \dfrac{w}{{{Q_1}}} = \dfrac{{{Q_1} - {Q_2}}}{{{Q_1}}}$
The efficiency of the Carnot engine depends on the absolute temperature of the sink and source. So
$ \Rightarrow \eta = \dfrac{w}{{{Q_1}}} = \dfrac{{{Q_1} - {Q_2}}}{{{Q_1}}} = \dfrac{{{T_1} - {T_2}}}{{{T_1}}}$.......... (1)
From this equation
$ \Rightarrow \dfrac{w}{{{Q_1}}} = \dfrac{{{T_1} - {T_2}}}{{{T_1}}}$
$ \Rightarrow {Q_1} = w\left( {\dfrac{{{T_1}}}{{{T_1} - {T_2}}}} \right)$
Step 2
Now we put all given value in this equation
$ \Rightarrow {Q_1} = 800\left( {\dfrac{{600}}{{600 - 300}}} \right)$
By solving this
$
\Rightarrow {Q_1} = 800\left( {\dfrac{{600}}{{300}}} \right) \\
\Rightarrow {Q_1} = 800\left( 2 \right) \\
$
$\therefore {Q_1} = 1600J$
Hence we get the heat given by source is ${Q_1} = 1600J$
In this question the option B is correct.
Note:
The efficiency of a Carnot engine is given by $ \Rightarrow \eta = \dfrac{w}{{{Q_1}}} = \dfrac{{{Q_1} - {Q_2}}}{{{Q_1}}} = \dfrac{{{T_1} - {T_2}}}{{{T_1}}}$ we can find the efficiency of this engine
$ \Rightarrow \eta = \dfrac{w}{{{Q_1}}} = \dfrac{{800}}{{1600}} = \dfrac{1}{2}$
The percentage efficiency of the engine is $ \Rightarrow \eta = \dfrac{1}{2} \times 100 = 50\% $
By this formula we can calculate all values associated with the Carnot engine.
To solve this question we have use formula of efficiency of carnot engine which is given by $\eta $
$\eta = \dfrac{w}{{{Q_1}}} = \dfrac{{{Q_1} - {Q_2}}}{{{Q_1}}} = \dfrac{{{T_1} - {T_2}}}{{{T_1}}}$
Where $w \Rightarrow $ work done by substance
${Q_1} \Rightarrow $ Heat taken from source
${Q_2} \Rightarrow $ Remaining heat given to sink
${T_1} \Rightarrow $ Temperature of source
${T_2} \Rightarrow $ Temperature of sink
Step by step solution:
Step 1
In a carnot engine substance take heat or energy from a source which is at temperature ${T_1}$ and change some amount of heat into work $w$ and remaining heat transfer to sink at temperature ${T_2}$ as shown in the diagram.

Efficiency of Carnot engine $\eta $ defined as the ratio of net work done $w$ by the engine during one cycle to the heat taken in from the source ${Q_1}$ in one cycle thus.
$ \Rightarrow \eta = \dfrac{w}{{{Q_1}}} = \dfrac{{{Q_1} - {Q_2}}}{{{Q_1}}}$
The efficiency of the Carnot engine depends on the absolute temperature of the sink and source. So
$ \Rightarrow \eta = \dfrac{w}{{{Q_1}}} = \dfrac{{{Q_1} - {Q_2}}}{{{Q_1}}} = \dfrac{{{T_1} - {T_2}}}{{{T_1}}}$.......... (1)
From this equation
$ \Rightarrow \dfrac{w}{{{Q_1}}} = \dfrac{{{T_1} - {T_2}}}{{{T_1}}}$
$ \Rightarrow {Q_1} = w\left( {\dfrac{{{T_1}}}{{{T_1} - {T_2}}}} \right)$
Step 2
Now we put all given value in this equation
$ \Rightarrow {Q_1} = 800\left( {\dfrac{{600}}{{600 - 300}}} \right)$
By solving this
$
\Rightarrow {Q_1} = 800\left( {\dfrac{{600}}{{300}}} \right) \\
\Rightarrow {Q_1} = 800\left( 2 \right) \\
$
$\therefore {Q_1} = 1600J$
Hence we get the heat given by source is ${Q_1} = 1600J$
In this question the option B is correct.
Note:
The efficiency of a Carnot engine is given by $ \Rightarrow \eta = \dfrac{w}{{{Q_1}}} = \dfrac{{{Q_1} - {Q_2}}}{{{Q_1}}} = \dfrac{{{T_1} - {T_2}}}{{{T_1}}}$ we can find the efficiency of this engine
$ \Rightarrow \eta = \dfrac{w}{{{Q_1}}} = \dfrac{{800}}{{1600}} = \dfrac{1}{2}$
The percentage efficiency of the engine is $ \Rightarrow \eta = \dfrac{1}{2} \times 100 = 50\% $
By this formula we can calculate all values associated with the Carnot engine.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




