
A boy 1.4 m tall casts a shadow 1.2 m long at the time when a building casts a shadow 5.4 m long. Find the height of the building?
Answer
534.3k+ views
Hint: Assume that the height of the building from the ground is ‘h’. First, draw a rough diagram of the situation given in the question and then use the formula $ \tan \theta =\dfrac{\text{perpendicular}}{\text{base}} $ in the right angle triangle with boy as its one side and substitute the given values to get the height to get the angle of elevation of the sum. Then move to the case of the building, in this case the angle of elevation of the sun is not changed, so use it to get the height of the building.
Complete step-by-step answer:
Let us start with the question by drawing a representative diagram of the case of the boy.
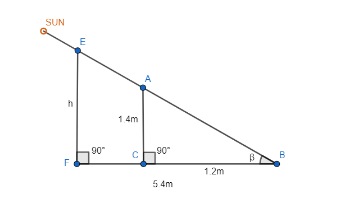
According to the above figure, AC is the boy and the shadow of the boy is represented by BC. In the figure the segment EF represents the building and its shadow is FB. Also, we have considered the angle of elevation of the sun to be constant and is denoted by $ \beta $ .
We have assumed the height of the building from the ground as ‘h’. Therefore, EF = h.
Now, in right angle triangle ABC,
We let $ \angle ABC=\beta $ .
We know that, $ \tan \theta =\dfrac{\text{perpendicular}}{\text{base}} $ . And it is given that the height of the boy is 1.4 m and the length of his shadow is 1.2 m. So, AC=1.4 m and BC=1.2 m.
$ \begin{align}
& \therefore \tan \beta =\dfrac{1.4}{1.2} \\
& \Rightarrow \tan \beta =\dfrac{7}{6}...........(i) \\
\end{align} $
Now, let us move to triangle EFB. In this triangle EF=h and FB=5.4m. So, again using $ \tan \theta =\dfrac{\text{perpendicular}}{\text{base}} $ , we can say:
$ \tan \beta =\dfrac{EF}{FB}=\dfrac{h}{5.4} $
Now, if we substitute the value of $ \tan \beta $ from equation (i), we get
$ \dfrac{7}{6}=\dfrac{h}{5.4} $
$ \Rightarrow \dfrac{7}{6}\times 5.4=h $
$ \Rightarrow h=6.3m $
Hence, we can conclude that the height of the tower is 6.3m.
Note: If you want you can solve the above question by using the properties of similar triangles as well. If you see in $ \Delta EBF $ and $ \Delta ABC $ , $ \angle B $ is common, both are right angled so, one more angle equal, and as 2 of the angles are equal third will also be equal. So, they are similar. Now we know the bases of both triangles, so find the ratio of the sides and as the ratio of the corresponding sides are equal, find the required result.
Complete step-by-step answer:
Let us start with the question by drawing a representative diagram of the case of the boy.

According to the above figure, AC is the boy and the shadow of the boy is represented by BC. In the figure the segment EF represents the building and its shadow is FB. Also, we have considered the angle of elevation of the sun to be constant and is denoted by $ \beta $ .
We have assumed the height of the building from the ground as ‘h’. Therefore, EF = h.
Now, in right angle triangle ABC,
We let $ \angle ABC=\beta $ .
We know that, $ \tan \theta =\dfrac{\text{perpendicular}}{\text{base}} $ . And it is given that the height of the boy is 1.4 m and the length of his shadow is 1.2 m. So, AC=1.4 m and BC=1.2 m.
$ \begin{align}
& \therefore \tan \beta =\dfrac{1.4}{1.2} \\
& \Rightarrow \tan \beta =\dfrac{7}{6}...........(i) \\
\end{align} $
Now, let us move to triangle EFB. In this triangle EF=h and FB=5.4m. So, again using $ \tan \theta =\dfrac{\text{perpendicular}}{\text{base}} $ , we can say:
$ \tan \beta =\dfrac{EF}{FB}=\dfrac{h}{5.4} $
Now, if we substitute the value of $ \tan \beta $ from equation (i), we get
$ \dfrac{7}{6}=\dfrac{h}{5.4} $
$ \Rightarrow \dfrac{7}{6}\times 5.4=h $
$ \Rightarrow h=6.3m $
Hence, we can conclude that the height of the tower is 6.3m.
Note: If you want you can solve the above question by using the properties of similar triangles as well. If you see in $ \Delta EBF $ and $ \Delta ABC $ , $ \angle B $ is common, both are right angled so, one more angle equal, and as 2 of the angles are equal third will also be equal. So, they are similar. Now we know the bases of both triangles, so find the ratio of the sides and as the ratio of the corresponding sides are equal, find the required result.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE




