




How Do Newton’s Rings Form? Physics, Diagrams & Applications
Newton's Ring Experiment is an optical phenomenon where a series of concentric bright and dark rings appear due to light interference between two surfaces—a convex lens and a flat glass plate. First investigated by Sir Isaac Newton in 1666, the phenomenon highlights the wave nature of light. Monochromatic light creates distinct alternating rings, while white light produces a rainbow-coloured pattern due to varying wavelengths interfering at different air gap thicknesses. On this page, you will learn about the History and Discovery of Newton's Rings, Theory and Formation of Newton's Rings and more.
History and Discovery of Newton's Rings
The phenomenon was initially described by Robert Hooke in 1665 in Micrographia. Isaac Newton, while studying light during the Great Plague in 1666, quantitatively analysed this effect and documented it in his treatise Opticks (1704). The rings are named in Newton's honour, though his interpretation of the phenomenon differed from modern wave theory.
What are Newton's Rings?
It is said that Newton's Rings are formed by the interference pattern between two surfaces caused by the light reflecting between them. There are two flat surfaces on either side of the sphere. In 1704, Isaac Newton described the effect in a treatise called Opticks based on his research. Newton's Rings are visible when viewed with monochromatic light as alternating bright and dark circles located at the point of contact between the two surfaces. The different wavelengths of light conflict at very different levels of thickness in the layer of air between the two surfaces when viewed in white light. This results in a pattern of a concentric circle of Rainbow colors.
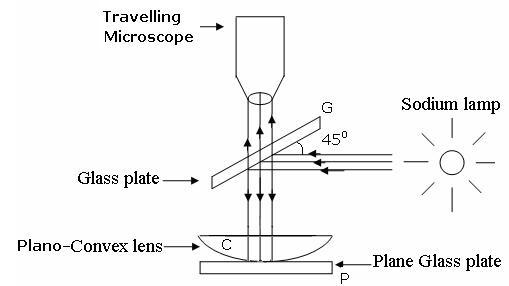
An Optical glass that has a flat surface is placed on a very slightly curved Convex glass to create the pattern. At other points, there is a slight air gap between the two surfaces of the two pieces of glass, which are in contact only at the center. The increasing distance between the center and the microscope is referred to as the radial distance. On the right side of one of the pieces, there is a small gap growing from left to right. In the monochromatic example, the source of colour is a monochromatic single source of light shining through the top piece and refracting off the bottom and top surfaces. In the resulting superposition, the two rays are combined.
This ray, however, generally travels a relatively long path as it reflects off the surface of the bottom. Two times the gap between the surfaces equals the additional path length.
A 180° phase reverse happens when the ray reflects off the bottom piece of glass. As a result, the phase reversal due to the internal reflection of the other ray from the underside of the top glass does not occur.
Newton's Ring Experiment Theory
Formation of Newton’s Rings
Light waves are interfered with to create Newton's Rings when Reflections occur between the top and bottom surfaces of the air film formed between the lens and glass sheet.
According to the theory of waves of light, the formation of Rings of Newton's can be explained as follows:
In between the glass sheet and lens is an air film of varying thickness.
Reflection and refractive rays occur simultaneously when a ray strikes the lens surface.
Rays that are refracted have a phase change of 180 on the reflection when they strike a glass sheet.
If the path difference between two waves is m+1/2*1, an interference happens constructively, while destructively if the path difference between them is ml. This produces alternate bright and dark Rings.
Key Concepts:
Air Film Thickness: The air gap increases radially from the centre, influencing interference.
Path Difference: Constructive interference occurs when the path difference equals an odd multiple of λ/2, while destructive interference happens at even multiples.
Phase Reversal: Reflection at the air-to-glass boundary causes a 180° phase shift.
Interference Patterns in Newton's Rings
Bright Rings:
Formed at points where the path difference between reflected rays equals $ \lambda/2$, resulting in constructive interference.Dark Rings:
Formed where the path difference equals 2nλ/2, resulting in destructive interference.Concentric Circles:
The varying air gap creates concentric fringes. In non-axially symmetric setups, the patterns take other shapes.
Quantitative Relationships in Newton's Rings
Radius of Bright Rings:
For monochromatic light with a dark center:
$r_N = \sqrt{\lambda R \left(N - \dfrac{1}{2}\right)}$
Where:$r_N$: Radius of the Nth bright ring
λ: Wavelength of light
R: Radius of curvature of the lens
N: Ring number
Air Gap Calculation:
The air gap (t) between the surfaces for a given radius (r) is:
$t = \dfrac{r^2}{2R}$.
Steps to Perform Newton's Ring Experiment Calculation
Measure Radii of Rings:
Use a travelling microscope to measure the diameters of several bright or dark rings. Half these values to get the radii.Determine the Difference Between Consecutive Rings:
Calculate the difference in the square of the radii of consecutive rings ($r_{N+1}^2 - r_N^2$).Apply Formulas for Desired Values:
Use the above formulas to calculate the wavelength of light (λ) or the air film thickness (t).
If the radius of curvature (R) is unknown, it can be determined using other experimental data.
Application of Newton's Ring
Measuring Wavelengths:
Newton's Rings provide a precise method to measure the wavelength of monochromatic light.Determining Lens Curvature:
The radius of curvature of a lens can be calculated using the ring pattern.Testing Surface Flatness:
The technique is used to detect surface irregularities as small as a fraction of the wavelength of light.Research in Optics:
It aids in studying interference, wave behaviour, and light reflection principles.
FAQs on Newton’s Rings: Definition, Formation & Key Concepts
1. What are Newton's rings and how are they formed in simple terms?
Newton's rings are a pattern of concentric bright and dark circles seen when a plano-convex lens is placed on a flat glass surface. They are formed due to the interference of light waves reflecting from the top and bottom surfaces of the thin air film trapped between the lens and the glass plate.
2. Why are Newton's rings perfectly circular in shape?
The rings are circular because the air film between the lens and the glass has a thickness that is the same at any given distance from the central point of contact. Since the lens is symmetrical, all points at an equal radius form a circle of equal air film thickness, resulting in a circular interference pattern.
3. What is the main cause for the alternating bright and dark rings in the pattern?
The alternating rings are a direct result of light wave interference.
- A bright ring appears where the reflected light waves interfere constructively (crests align with crests).
- A dark ring appears where the waves interfere destructively (crests align with troughs), cancelling each other out.
4. Why is the very centre of Newton's rings a dark spot and not a bright one?
The centre is dark because at the point of contact, the air film thickness is almost zero. However, light reflecting from the bottom glass plate undergoes a phase shift of 180° (or a path difference of λ/2). This phase shift causes the two reflecting rays to be out of phase, leading to destructive interference and creating a dark spot right at the centre.
5. Why must we use a single-colour (monochromatic) light source to see clear rings?
A monochromatic light source, like a sodium lamp, has a single, constant wavelength. This creates a clear and stable pattern of bright and dark rings. If white light were used, which contains many different wavelengths, each colour would form its own set of rings at slightly different positions, causing them to overlap and appear as a blurry, coloured smear instead of distinct rings.
6. What are some real-world applications of Newton's rings?
The principle behind Newton's rings is primarily used in optics for precision measurements. For example, it can be used to:
- Test the flatness of a surface by checking for any distortions in the ring pattern.
- Determine the radius of curvature of a lens with high accuracy.
- Measure the wavelength of a monochromatic light source.
7. How does the spacing between the rings change as you move away from the centre?
As you move outwards from the centre, the spacing between the rings decreases. The rings become progressively closer to each other. This is because the radius of the rings is proportional to the square root of the ring number, not the number itself, causing the gap between them to shrink for higher-order rings.
8. What would happen to the rings if a liquid like water was introduced between the lens and the glass plate?
If water or another transparent liquid were introduced, the rings would shrink and become closer together. This is because the wavelength of light decreases when it enters a denser medium like water. This change in wavelength alters the conditions for interference, causing the entire pattern to contract.





















