




Key Equations and Concepts in Maxwell's Theory of Electromagnetism
Explore the Electromagnetic Wave Theory Of Maxwell, its fundamental principles, mathematical framework, and real-world applications. Learn how James Clerk Maxwell’s revolutionary equations unified electricity, magnetism, and light, forming the foundation of modern physics and wireless technology. Discover essential formulas and derivations, and see why this theory is still central to science today.
Understanding the Electromagnetic Wave Theory Of Maxwell
The Electromagnetic Wave Theory Of Maxwell, also known as the electromagnetic wave theory of James Clerk Maxwell, marks a pivotal moment in physics. Maxwell’s insight was to realize that changing electric fields produce changing magnetic fields and vice versa, resulting in self-propagating waves—electromagnetic waves—that travel at the speed of light. This elegant concept unified electricity, magnetism, and optics into what we now call Maxwell’s theory of electromagnetism, fundamentally shifting how scientists perceive light and radiation.
Consider flipping a magnet near a wire or turning a coil in a magnetic field—Maxwell’s electromagnetic theory of light explains these phenomena by showing how electric and magnetic fields interact continuously. Because these fields can exist and oscillate even in a vacuum, electromagnetic waves like light, radio, X-rays, and microwaves travel through space without any material medium, as proven by Maxwell wave theory.
Core Principles of Maxwell’s Electromagnetic Wave Theory
Maxwell’s electromagnetic theory of light introduced several important postulates that explain both the nature and propagation of electromagnetic waves:
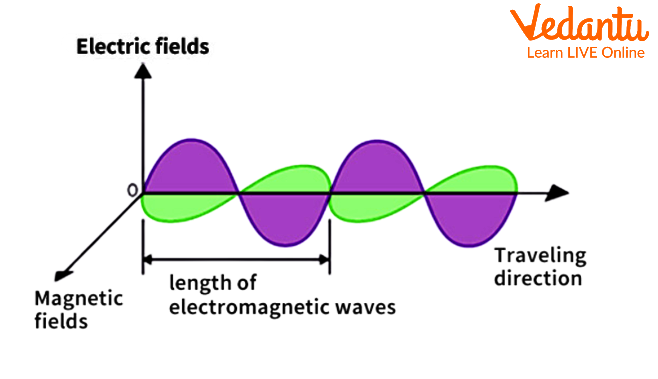
- Light and all electromagnetic radiation are forms of oscillating electric and magnetic fields perpendicular to each other and to the direction of travel.
- Radiant energy is released continuously as electromagnetic waves from all sources.
- Electromagnetic waves do not require any material medium and can propagate through a vacuum.
- All electromagnetic waves propagate at the same speed in a vacuum, $c ≈ 3 \times 10^8$ m/s.
- The energy of these waves depends on their frequency (higher frequency, higher energy).
Mathematical Formulation: Maxwell’s Equations and the Wave Equation
Maxwell’s electromagnetic theory formula is encapsulated in four elegant equations, often called the Maxwell 4 equations explained. These equations form the backbone of electromagnetic waves Maxwell equations and are responsible for the propagation of electromagnetic waves in space:
- Gauss’s Law for Electricity: $\nabla \cdot E = \dfrac{\rho}{\varepsilon_0}$
- Gauss’s Law for Magnetism: $\nabla \cdot B = 0$
- Faraday’s Law of Induction: $\nabla \times E = -\dfrac{\partial B}{\partial t}$
- Ampere-Maxwell Law: $\nabla \times B = \mu_0 J + \mu_0\varepsilon_0\dfrac{\partial E}{\partial t}$
From these, the electromagnetic wave equation can be derived. For the electric field $E$ (a similar form exists for the magnetic field $B$):
Here: $c = \dfrac{1}{\sqrt{\mu_0 \varepsilon_0}}$ is the speed of light in vacuum.
Step-by-Step: Maxwell Wave Equation Derivation
- Start with Maxwell’s equations in free space (no charges, $\rho = 0$ and $J = 0$).
- Take the curl of Faraday’s Law: $\nabla \times (\nabla \times E) = -\dfrac{\partial}{\partial t}(\nabla \times B)$
- Apply the vector identity: $\nabla \times (\nabla \times E) = \nabla(\nabla \cdot E) - \nabla^2 E$
- Since $\nabla \cdot E = 0$ in vacuum, we get $-\nabla^2 E = -\dfrac{\partial}{\partial t}(\nabla \times B)$
- Use Ampere-Maxwell Law in vacuum: $\nabla \times B = \mu_0\varepsilon_0 \dfrac{\partial E}{\partial t}$
- Substitute to get: $-\nabla^2 E = -\mu_0\varepsilon_0 \dfrac{\partial^2 E}{\partial t^2}$
- Finally, rearrange: $\nabla^2 E = \mu_0\varepsilon_0 \dfrac{\partial^2 E}{\partial t^2}$
- Or: $\left( \dfrac{1}{c^2} \dfrac{\partial^2}{\partial t^2} - \nabla^2 \right) E = 0$
This derivation shows how electromagnetic waves arise naturally from Maxwell’s equations—a key highlight in every Maxwell electromagnetic theory PDF and Maxwell's equations derivation PDF.
Symbols and Quantities in Maxwell’s Theory
| Symbol | Physical Quantity | Description |
|---|---|---|
| E | Electric Field | Field exerting force on charges |
| B | Magnetic Field | Field affecting moving charges & magnets |
| $\varepsilon_0$ | Permittivity of Free Space | Measures how electric fields spread in vacuum |
| $\mu_0$ | Permeability of Free Space | Measures how magnetic fields form in vacuum |
| $c$ | Speed of Light | $3 \times 10^8$ m/s in vacuum |
| $\rho$ | Charge Density | Amount of electric charge per unit volume |
| J | Current Density | Current per unit area |
Understanding these quantities is crucial to unlocking the power of Maxwell’s theory of atom and modern electromagnetism.
Applications of Maxwell’s Electromagnetic Wave Theory
The impact of Maxwell wave theory goes far beyond theoretical physics. Here are some familiar and groundbreaking uses:
- Wireless communication: mobile phones, Wi-Fi, radio, and satellite signals all rely on electromagnetic waves Maxwell equations predicted.
- Broadcasting: TV and radio signals are transmitted as electromagnetic waves.
- Medical imaging: X-rays and MRI use different parts of the electromagnetic spectrum, explained through Maxwell's electromagnetic theory of light.
- Household technology: Microwave ovens and remote controls make use of electromagnetic radiation, directly utilizing modulation principles derived from Maxwell’s theory.
These applications highlight why Maxwell’s theory is often called the “grand unification” of classical physics and why resources like electromagnetic wave theory Kong PDF and Maxwell equations PDF remain essential.
Limitations of Maxwell’s Electromagnetic Wave Theory
Despite its vast success, Maxwell’s theory could not explain certain phenomena accurately at the atomistic and quantum scales, leading to quantum physics breakthroughs. Specifically, it fails to account for:
- The spectrum of black body radiation.
- The photoelectric effect, explained by Einstein using the concept of photons or light quanta.
- Variation of heat capacity in solids at different temperatures.
- Discrete line spectra of atoms, notably seen in hydrogen atoms.
Nonetheless, Maxwell’s theory forms a robust platform for classical electromagnetism.
Maxwell’s Physics in Everyday Life and Beyond
The electromagnetic wave theory of Maxwell is present all around us—from visible light energy enabling vision to the invisible fields behind the workings of electric force. Maxwell’s work also paved the way for scientists like Hertz, who experimentally verified electromagnetic waves, confirming the How did James Clerk Maxwell discover electromagnetic waves story.
If you want to learn more about the people behind the equations, visit this resource about famous physicists.
Summary: Why Maxwell’s Electromagnetic Wave Theory Matters
The Electromagnetic Wave Theory Of Maxwell, unifying electric and magnetic fields and identifying light as an electromagnetic wave, remains one of humanity’s most significant intellectual achievements. Despite later advancements like quantum theory, Maxwell’s four equations are still integral to our understanding of fields, waves, and modern technology. To strengthen your grasp on related topics, review physics formulas for Class 12 and Faraday’s Law.
Continue your physics journey with Maxwell’s electromagnetic wave theory and uncover its connections to everything from oscillatory motion to cutting-edge wireless communications.
FAQs on Understanding Maxwell's Electromagnetic Wave Theory
1. What is Maxwell's electromagnetic wave theory?
Maxwell's electromagnetic wave theory states that light and other electromagnetic radiations are produced by oscillating electric and magnetic fields that propagate through space as waves.
Key points include:
- Light is an electromagnetic wave made of oscillating electric and magnetic fields.
- Electric and magnetic fields are perpendicular both to each other and to the direction of wave propagation.
- These waves can travel through a vacuum, unlike sound waves.
2. What are the main postulates of Maxwell’s electromagnetic wave theory?
Maxwell’s theory includes several foundational postulates about light and electromagnetic waves:
- Light is an electromagnetic wave caused by accelerated electric charges.
- Electric and magnetic fields generated by charges vary together and propagate as waves.
- The direction of the wave is perpendicular to both electric and magnetic fields.
- Electromagnetic waves travel at the speed of light (3 × 108 m/s in a vacuum).
3. What is the significance of Maxwell's electromagnetic wave theory for the understanding of light?
Maxwell's theory revolutionized the understanding of light as an electromagnetic wave, connecting optics with electricity and magnetism.
Importance:
- Proves that light doesn’t require a medium (like ether) to travel.
- Explains light phenomena such as reflection, refraction, and polarization using electromagnetic concepts.
- Lays the foundation for modern physics and technology, including wireless communication, radio, and TV.
4. What are the key equations in Maxwell’s electromagnetic theory?
The four Maxwell's equations mathematically describe electromagnetic fields and their behavior:
- Gauss’s Law for Electricity
- Gauss’s Law for Magnetism
- Faraday’s Law of Electromagnetic Induction
- Ampère-Maxwell Law
5. How do electromagnetic waves propagate according to Maxwell?
According to Maxwell's theory, electromagnetic waves propagate through the continuous generation of changing electric and magnetic fields.
They travel by:
- A changing electric field creates a changing magnetic field.
- The changing magnetic field, in turn, produces a changing electric field.
- This mutual generation allows the wave to travel through free space at light speed.
6. What are the characteristics of electromagnetic waves predicted by Maxwell?
Maxwell predicted several important characteristics of electromagnetic waves:
- They are transverse waves (fields oscillate perpendicular to direction of motion).
- They can travel through vacuum.
- Travel at the speed of light in vacuum.
- Their energy is shared equally between electric and magnetic fields.
7. What are the differences between electromagnetic waves and mechanical waves?
Electromagnetic waves and mechanical waves differ in several ways:
- Electromagnetic waves can travel through vacuum; mechanical waves need a material medium.
- Electromagnetic waves are made of electric and magnetic fields; mechanical waves involve particles oscillating in a medium.
- Electromagnetic waves always travel at the speed of light in vacuum, whereas mechanical wave speed depends on the medium.
8. Who formulated the electromagnetic wave theory and what was his contribution?
James Clerk Maxwell formulated the electromagnetic wave theory in the 19th century.
His major contributions were:
- Unified the concepts of electricity and magnetism into one: electromagnetism.
- Predicted the existence of electromagnetic waves, including light.
- Showed mathematically how changing electric and magnetic fields propagate.
9. How did Maxwell’s electromagnetic wave theory lead to technological advancements?
Maxwell’s theory paved the way for numerous innovations by proving the existence of electromagnetic waves:
- Enabled invention of wireless technologies like radio, radar, and television.
- Promoted further research, leading to microwaves, infrared, ultraviolet, and X-rays.
- Set the groundwork for modern communication networks and electronics.
10. What experimental evidence supports Maxwell’s electromagnetic wave theory?
Experimental confirmation of Maxwell's wave theory was provided mainly by Heinrich Hertz in 1887.
Key evidence:
- Generation and detection of electromagnetic waves in laboratory conditions.
- Observed that radio waves behaved like light waves (reflection, refraction, polarization).
- The measured speed of radio waves matched the speed of light, as predicted by Maxwell.
11. Give two applications of electromagnetic waves in daily life.
Electromagnetic waves are essential in modern life:
- Radio and TV broadcasting (communication via radio waves).
- Microwave ovens (heating food using microwaves).
12. What are the limitations of Maxwell’s electromagnetic wave theory?
While Maxwell's theory explains most properties of electromagnetic waves, it cannot explain the quantum nature of light such as the photoelectric effect.
- Fails to account for energy quantization.
- Does not explain the particle-like behavior of light (photons).























