




Bragg's Law Formula and Equation: nλ = 2d sinθ Explained
Braggs Law represents a fundamental principle in crystallography that describes the conditions necessary for constructive interference when X-rays interact with crystal lattice planes. Named after father-son duo William Henry and William Lawrence Bragg, this law enables scientists to determine crystal structures, interplanar distances, and identify unknown materials through X-ray diffraction techniques. Understanding Bragg's law equation and its applications is essential for students studying solid-state physics and material science.
Understanding Bragg's Law of Diffraction
When X-rays encounter a crystalline material, they interact with atoms arranged in regular, repeating patterns called crystal lattices. Bragg's law describes the geometric conditions under which these scattered X-rays interfere constructively to produce measurable diffraction patterns. The phenomenon occurs when X-rays reflect from parallel planes of atoms within the crystal structure.
For constructive interference to occur, the path difference between X-rays reflected from adjacent crystal planes must equal an integer multiple of the X-ray wavelength. This condition ensures that reflected waves remain in phase, producing intense diffraction peaks that can be detected and analyzed.
Bragg's Law Formula and Equation
The mathematical expression of Bragg's law relates the wavelength of incident X-rays to the interplanar spacing and angle of incidence:
Where:
- $n$ represents the order of diffraction (positive integer: 1, 2, 3...)
- $\lambda$ is the wavelength of incident X-rays
- $d$ denotes the interplanar spacing between crystal lattice planes
- $\theta$ is the angle of incidence (glancing angle)
What is n in Bragg's Law?
The parameter $n$ in Bragg's law equation represents the order of diffraction, indicating how many wavelengths fit into the path difference between rays reflected from successive crystal planes. First-order diffraction ($n = 1$) produces the strongest intensity peaks, while higher orders ($n = 2, 3$...) generate progressively weaker reflections.
What is d in Bragg's Law?
The d-spacing parameter represents the perpendicular distance between parallel atomic planes in the crystal lattice. Each set of crystal planes possesses a characteristic d-spacing value that depends on the crystal structure, atomic arrangement, and unit cell dimensions. Different materials exhibit unique d-spacing patterns, making this parameter crucial for material identification.
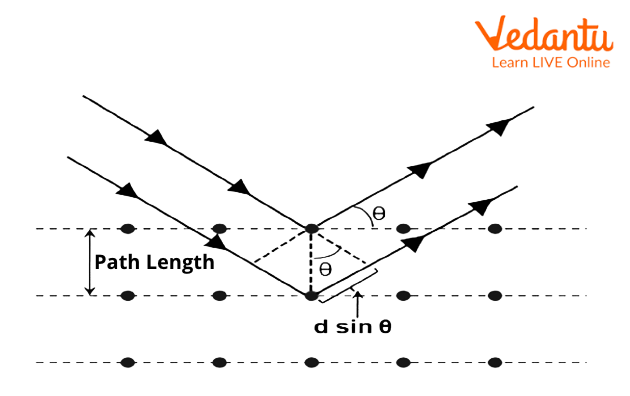
Bragg's Law Derivation
The derivation of Bragg's law statement involves analyzing the geometric relationship between incident X-rays and crystal lattice planes:
- Consider parallel X-ray beams striking adjacent crystal planes separated by distance $d$
- The incident angle equals the reflection angle (specular reflection): $\theta_{incident} = \theta_{reflected}$
- Calculate the path difference between rays reflected from consecutive planes: $\Delta = 2d\sin\theta$
- For constructive interference, this path difference must equal integer multiples of wavelength: $\Delta = n\lambda$
- Combining these conditions yields the final Bragg's law formula: $n\lambda = 2d\sin\theta$
Applications in X-ray Diffraction (XRD)
Bragg's Law X-ray diffraction finds extensive applications in materials characterization and structural analysis. In XRD experiments, researchers use crystals with known d-spacings as analyzing components in spectrometers.
Material Identification Through Bragg's Law
In X-ray diffraction analysis, scientists keep the incident wavelength constant while measuring diffraction angles where constructive interference occurs. By applying Bragg's law calculator principles, they determine the d-spacing values for unknown crystal samples. Each crystalline material produces a unique "fingerprint" pattern of d-spacings, enabling precise identification.

Wavelength Dispersive Spectrometry
In wavelength dispersive spectrometry (WDS) and X-ray fluorescence spectroscopy, analyzing crystals with predetermined d-spacings serve as monochromators. The crystal orientation adjusts according to Bragg's law to direct specific wavelengths toward detectors for quantitative elemental analysis.
Every element in the periodic table emits characteristic X-ray wavelengths corresponding to electronic transitions between atomic shells (K, L, M). By positioning the analyzing crystal at precise angles calculated using Bragg's law explained principles,
FAQs on What is Bragg's Law? Complete Guide to X-ray Diffraction
1. What is Bragg's Law in physics?
Bragg's Law relates the angles at which X-rays are diffracted by the planes in a crystalline material, helping measure crystal structures.
- Expressed as nλ = 2d sin θ, where n is an integer (order of reflection), λ is the wavelength, d is the distance between lattice planes, and θ is the angle of incidence.
- It forms the basis of X-ray crystallography and is essential for understanding how crystalline substances scatter X-rays.
- Key terms: diffraction, lattice planes, crystal structure.
2. State the formula for Bragg's Law and explain its terms.
Bragg's Law is mathematically given as nλ = 2d sin θ, where each term has a specific meaning:
- n: Order of diffraction (integer value, 1,2,3...)
- λ: Wavelength of incident X-ray
- d: Distance between two adjacent crystal planes
- θ: Angle between incident X-ray and crystal plane
3. What are the applications of Bragg's Law?
Bragg's Law is widely used in studying crystal structures and materials. Main applications include:
- X-ray crystallography to determine atomic structure of crystals
- Quality control in materials science
- Identification of unknown substances through X-ray diffraction patterns
- Development of new drugs by analyzing biomolecular structures
- Examination of metals, minerals, and semiconductors
4. How does Bragg's Law help in determining crystal structure?
Bragg's Law enables scientists to calculate the spacing between crystal planes by analyzing X-ray diffraction.
- X-rays are directed at a crystal, producing reflected beams at specific angles.
- Measuring these angles and intensities, and using the formula, reveals the arrangement of atoms within the crystal.
- Key concepts: interplanar distance, diffraction maxima, crystal geometry.
5. Who discovered Bragg's Law?
Bragg's Law was discovered by Sir William Henry Bragg and his son Sir William Lawrence Bragg in 1913.
- Their discovery helped launch the field of X-ray crystallography.
- The Braggs won the Nobel Prize in Physics in 1915.
6. What is meant by constructive interference in Bragg's Law?
Constructive interference in the context of Bragg's Law occurs when the path difference between X-rays reflected from successive crystal planes equals an integer multiple of the wavelength.
- This results in a strong reflected X-ray beam (bright spot).
- Condition: nλ = 2d sin θ.
- Related terms: diffraction maxima, phase difference.
7. How is Bragg's Law experimentally verified?
Bragg's Law is verified using X-ray diffraction experiments, such as the rotating crystal method.
- X-rays are passed through a crystal sample.
- Diffracted beams are detected at various angles.
- The measured angles match those predicted by the formula, confirming the law's validity.
8. What are the limitations of Bragg's Law?
Bragg's Law has certain limitations in its application.
- Assumes perfect and infinite crystals (real crystals have defects).
- Does not account for multiple scattering (secondary diffraction).
- Limited to crystalline (ordered) substances, not amorphous materials.
- Applicable mainly to monochromatic (single wavelength) X-rays.
9. What factors affect the intensity of diffracted X-rays in Bragg's Law?
The intensity of diffracted X-rays depends on several factors:
- Structure factor (atomic arrangement)
- Crystal orientation and quality
- Wavelength and energy of the incident X-rays
- Thickness of the crystal
- Absorption and thermal vibrations
10. Why is Bragg's Law important for students studying physics and chemistry?
Bragg's Law is crucial because it helps explain how scientists determine the structure of solids at the atomic level.
- Foundation of X-ray crystallography and solid-state physics
- Essential for understanding materials, minerals, and biological macromolecules
- Regularly featured in CBSE and other exam syllabi
- Supports concepts in both chemistry and physics















