




An Introduction to Bernoulli’s Theorem
Bernoulli’s theorem is the principle of energy conservation for perfect fluids in steady or streamlined flow. The fluid dynamics discussed by Bernoulli's theorem include how the fluid pressure varies with the flow velocity. The theorem was developed by Daniel Bernoulli, a Swiss mathematician in 1738. Leonard Euler created the Bernoulli equation that is still in use today despite Daniel Bernoulli having identified the underlying idea.
History of Daniel Bernoulli
Daniel Bernoulli (1700–1782) was a Dutch scientist who studied in Italy before settling in Switzerland. He was born into a family of mathematicians, his father, Johann Bernoulli, was one of the early pioneers of calculus, and his uncle, Jacob Bernoulli, was the first to discover probability theory.

Daniel Bernoulli (1700–1782),
Bernoulli's Principle
Bernoulli’s theorem, also known as Bernoulli’s principle, states that the whole mechanical energy of the moving fluid, which includes gravitational potential energy of elevation, fluid pressure energy, and kinetic energy of fluid motion, remains constant.
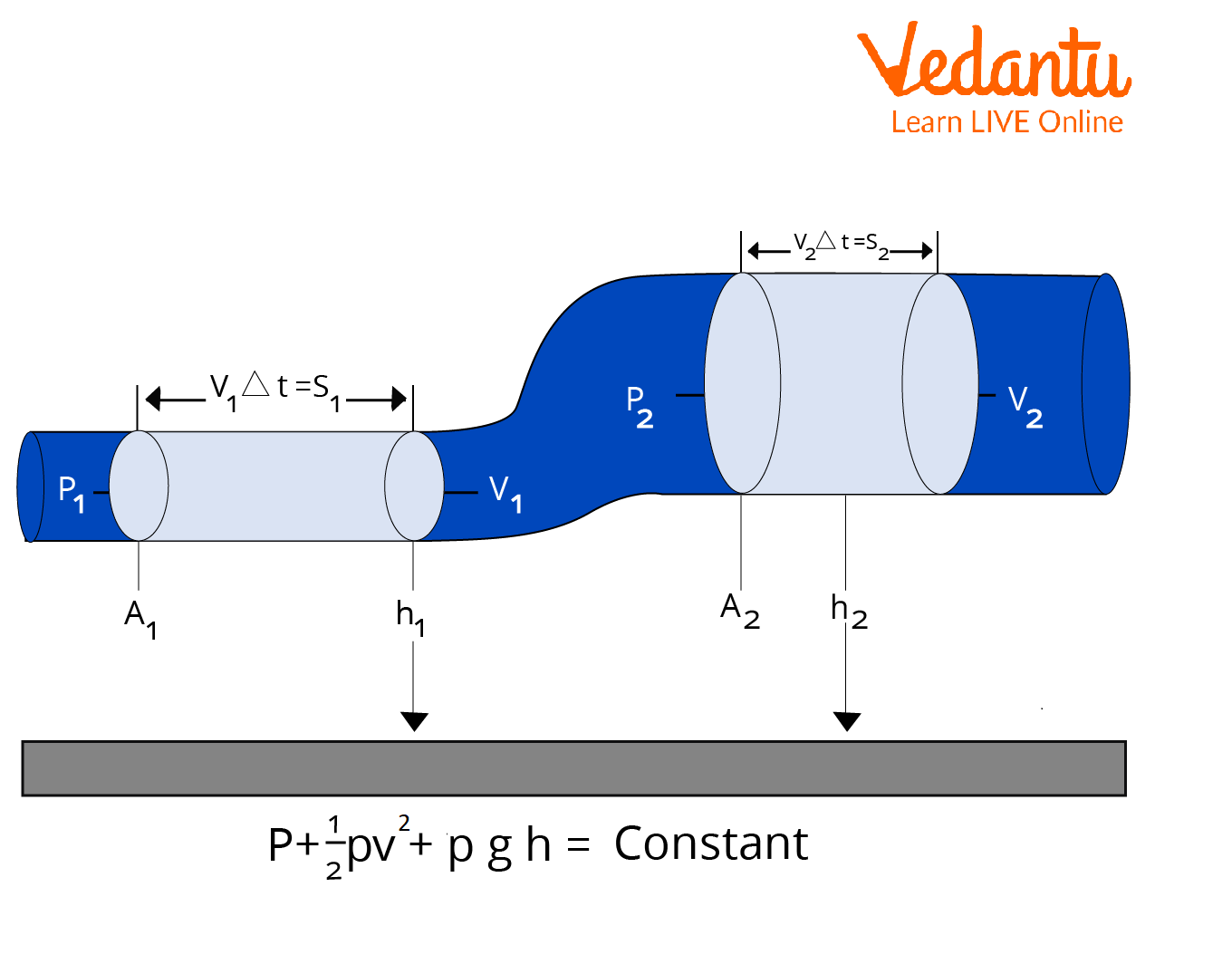
Bernoulli Equation
Assumption of Bernoulli's Theorem
The assumptions made to derive Bernoulli’s equation are as follows:
The fluid is excellent or perfect, with zero viscosity.
The flow is constant.
While flowing, there is no energy loss.
It is not possible to compress the flow.
Irrotational flow is present.
Except for gravity, there is no external force acting on the liquid.
Limitations of Bernoulli’s Theorem
The velocity of each liquid component moving through each cross-section of the pipe has been assumed to be uniform to derive the Bernoulli equation. It is not true actually.
This formula is ineffectual in turbulent or non-steady flows.
This theorem is typically used for low viscosity fluids.
Application of Bernoulli Theorem
Some of the important applications of Bernoulli’s theorem are given below:
One of Bernoulli's theorem applications is that it is used to solve any problems involving incompressible fluid flow.
Venturimeter is a tool that utilises Bernoulli's theorem to gauge the flow rate of the liquid via pipes. It is made up of a skinny coaxial tube B that joins two identical coaxial tubes A and C. To gauge the pressure of the next liquid, two vertical tubes D and E are installed on tubes A and B.
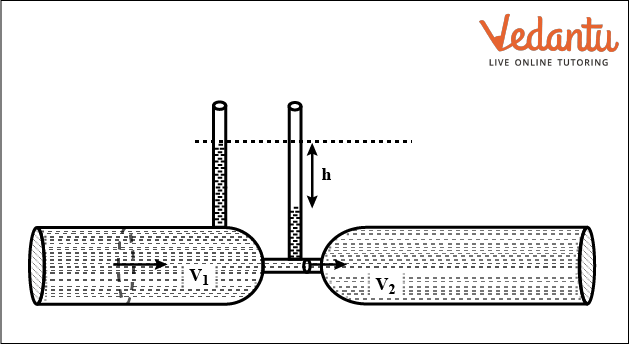
Venturimeter
When a liquid flows through tube ABC, part B will experience a higher flow velocity than either tube A or C. Therefore, component B's pressure will be lower than that of tubes A or C. It is possible to determine the rate of flow of the liquid in the tube by measuring the pressure differential between A and B.
An aircraft's airspeed can be calculated using its static port and Pitot tube. The airspeed indicator is calibrated using Bernoulli's principle to show the indicated airspeed that corresponds to the dynamic pressure.
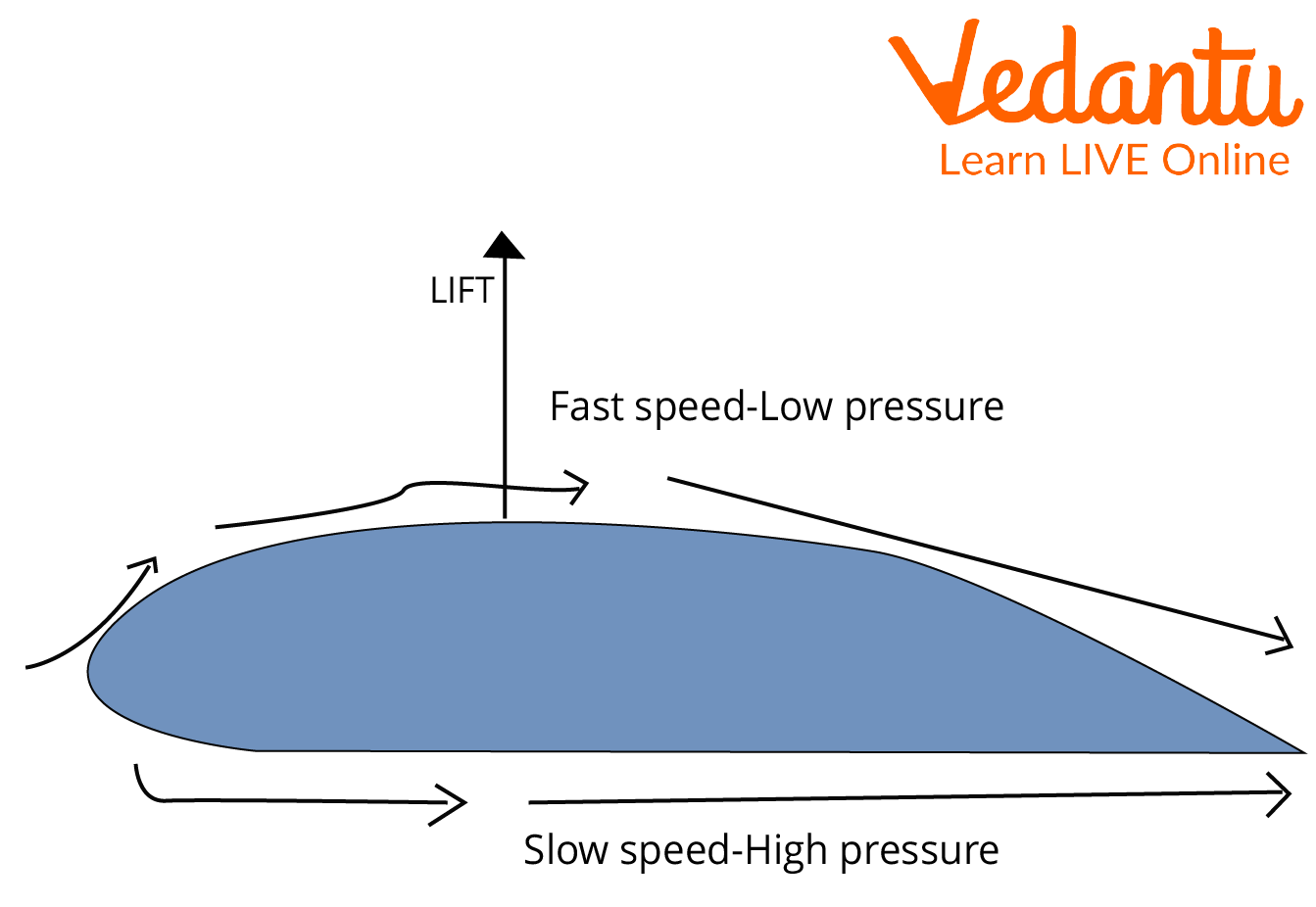
Aeroplane’s Wing
When using a bunsen burner, the gas leaves the nozzle quickly, which causes the pressure in the stem to drop. Consequently, fresh air from outside enters the burner through an air vent, and the resulting mixture of gas and air produces a blue flame.
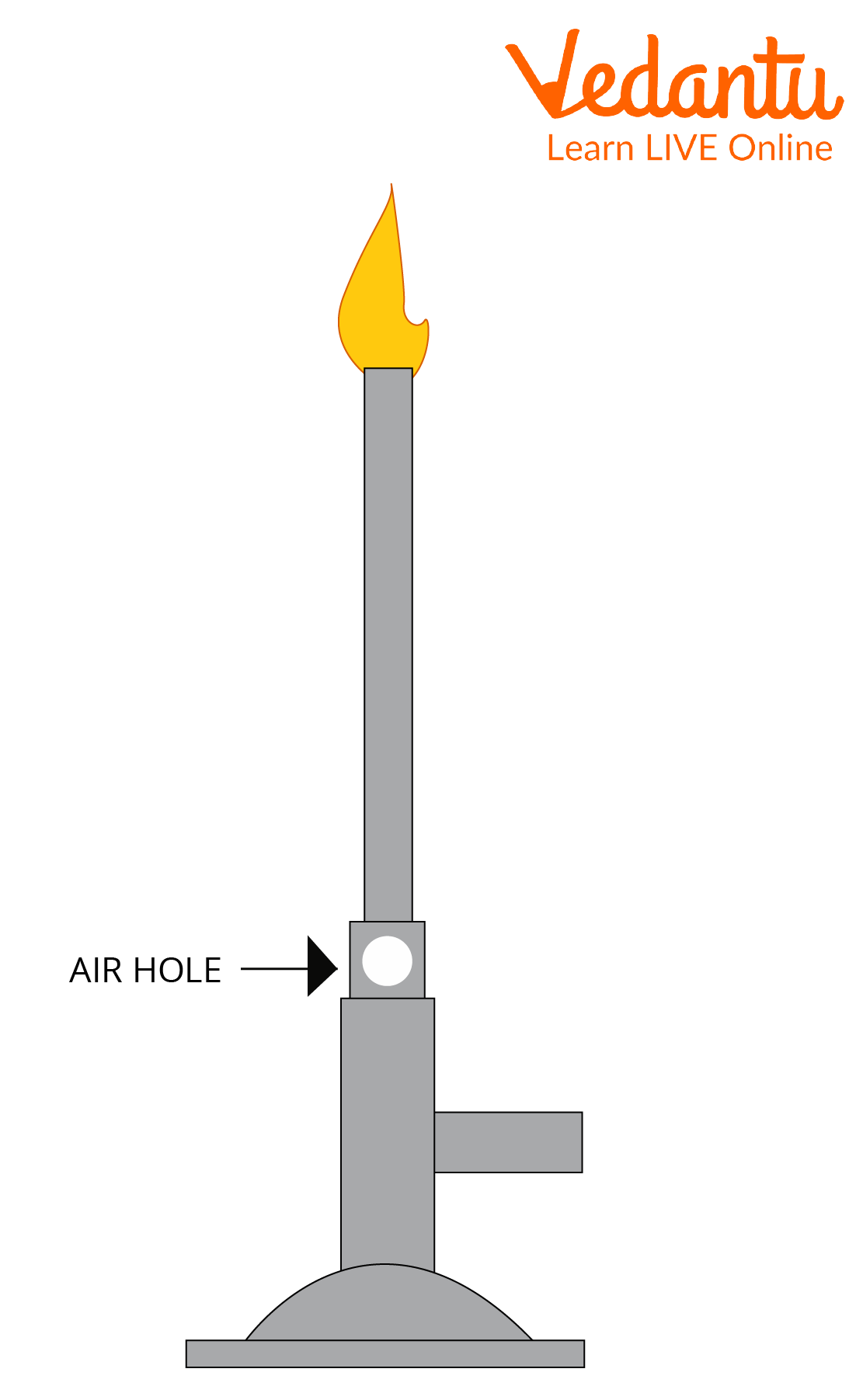
Bunsen Burner
Solved Examples
1. What are examples that use the Bernoulli principle?
Venturi metre
Mosquito Sprayers
Barometer
Thermometer
Ans. The following claims are based on Bernoulli's principle:
Venturi metre
Mosquito spray
A barometer using hydrostatic pressure.
Alcohol-based on expansion or a mercury thermometer
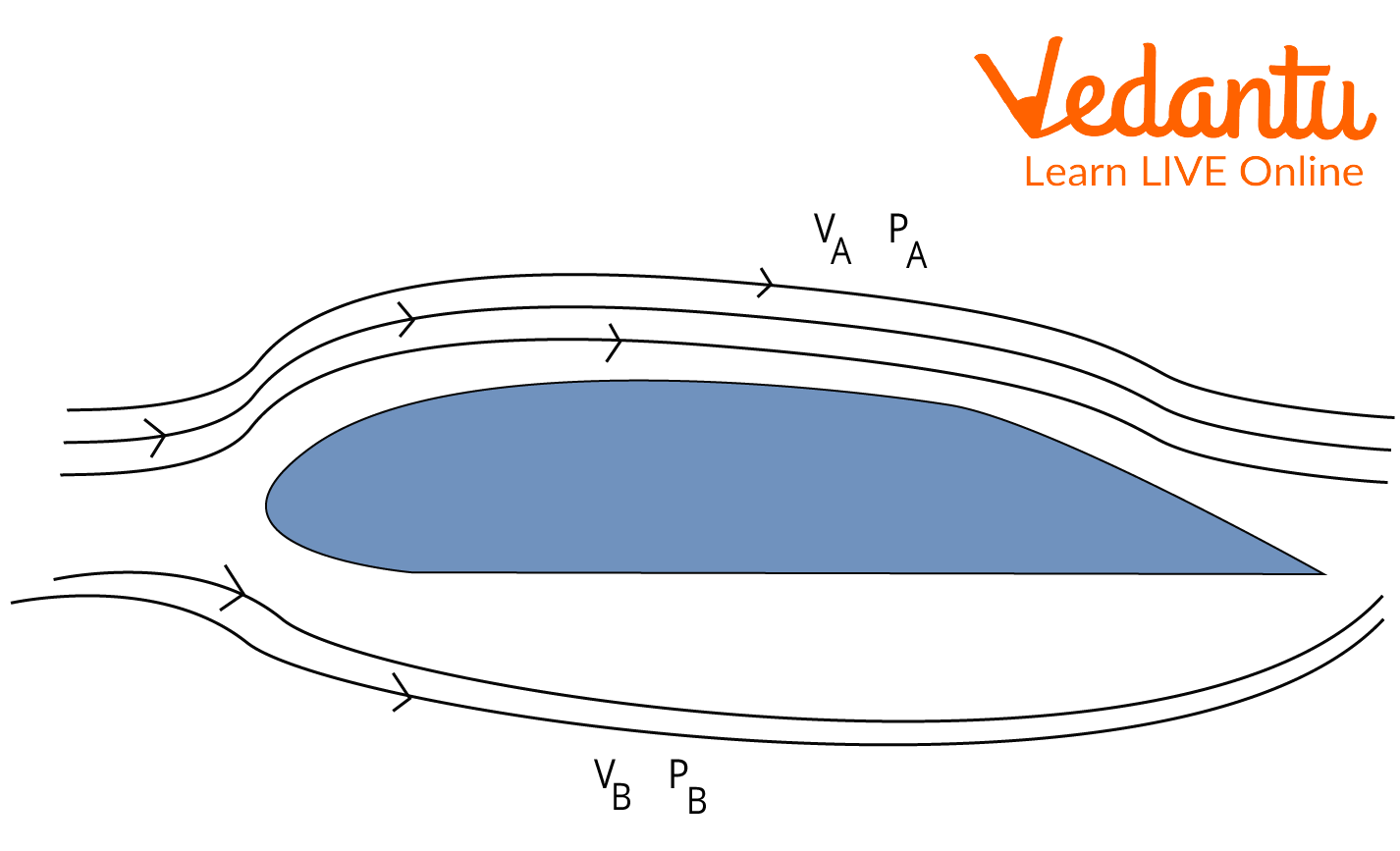
Streamlined Body
Ans. It is given that v is the air flow's velocity and P is the air pressure.
The air thrust at the bottom of the wing must be greater than the thrust force at the top of the wing for the plane's wings to lift upward.
When the air pressure at the bottom of the wing is higher, there is a greater thrust force on the underside of the wing. The pressure of P is exactly proportional to F, and its equation is \[P = F/A\]. When the pressure is higher, the force also rises. According to Bernoulli's principle, when the air velocity near the bottom of the wing is low, the air pressure there is high.
\[\begin{array}{l}{V_A} > {V_B}\\\therefore {P_A} < {P_B}\end{array}\]
Important Points
This formula is only for perfect fluids in steady or streamlined flow.
Bernoulli's theorem says, slower flowing fluids generate more pressure than faster moving fluids.
Conclusion
Bernoulli's theorem explains the connection between pressure, velocity, and elevation in a flowing liquid or gas. The principle gives insight into a variety of applications. The best approach to grasp these various applications is to have an open debate about the idea itself.
FAQs on Bernoulli’s Principle
1. What is Bernoulli’s Principle and how does it explain the relationship between pressure and velocity in fluids?
Bernoulli’s Principle states that in a steady, incompressible flow of a perfect fluid, the total mechanical energy (potential energy, pressure energy, and kinetic energy) remains constant. This means that when the velocity of the fluid increases, its pressure decreases, and vice versa. This relationship can be observed in the flow of air over airplane wings, where faster moving air results in lower pressure above the wing, causing lift.
2. What are the key assumptions made in deriving Bernoulli’s Equation as per the CBSE syllabus?
The derivation of Bernoulli’s Equation relies on several critical assumptions:
- The fluid is perfect or ideal (zero viscosity)
- The flow is steady and continuous
- There is no loss of energy in the flow
- The fluid is incompressible
- The flow is irrotational
- No external force acts on the fluid except gravity
3. Can you list important real-world applications of Bernoulli’s Theorem relevant to board exams?
Bernoulli’s Theorem has several notable applications including:
- Measurement of fluid flow rates using a Venturimeter
- Lift generation on airplane wings
- Functioning of Bunsen burners
- Spraying of insecticides using sprayers
- Design of carburetors in engines
4. Why does Bernoulli’s Principle fail for real, viscous fluids or turbulent flows?
Bernoulli’s Principle assumes ideal, non-viscous fluids and steady, streamlined flow. In reality, most fluids have viscosity and may experience turbulence, leading to energy loss due to friction. Therefore, the principle does not accurately predict pressure-velocity relationships in such cases because the total mechanical energy is not conserved due to dissipative forces.
5. How does a Venturimeter use Bernoulli’s Equation to measure flow rate?
A Venturimeter measures the flow rate in a pipe by creating a change in velocity at a constricted section of the tube. According to Bernoulli's Equation, the difference in pressure between the wider and narrower sections allows calculation of the fluid's velocity and hence the flow rate, since the pressure drop corresponds to an increase in kinetic energy.
6. What is the significance of Bernoulli’s effect in daily phenomena, such as why airplane wings generate lift?
Bernoulli’s effect explains that airflow above the curved upper surface of an airplane wing is faster than below it. This speed difference results in lower pressure above the wing and higher pressure below, producing an upward lift force. This principle is fundamental in aerodynamics and explains how birds and airplanes fly.
7. Explain why the velocity at different points in a pipe affects the pressure as per Bernoulli’s Principle.
When fluid flows from a wider to a narrower section of a pipe, its velocity increases. According to Bernoulli’s Principle, as velocity increases, pressure decreases. This inverse relationship ensures that the total energy per unit volume remains constant along the streamline, which is a direct consequence of energy conservation in fluid movement.
8. What are common misconceptions students have about Bernoulli’s Principle during board exams?
Common misconceptions include assuming that pressure and velocity are always inversely related in all situations, not recognizing the requirement of a steady, non-viscous, incompressible flow, and ignoring energy losses in real systems. Understanding the conditions for the application of the principle is crucial for correct answers in exams.
9. How is Bernoulli’s Principle applied in mosquito sprayers and Bunsen burners?
Both devices use the pressure drop created by high-speed fluid flow to draw another fluid (like air or liquid). In mosquito sprayers, liquid insecticide is drawn up and atomized by the fast-moving air. In Bunsen burners, rapid gas flow lowers the pressure and draws air into the burner, supporting efficient combustion.
10. What are important points to remember about Bernoulli’s Principle for the CBSE 2025–26 board exams?
Key points include:
- Bernoulli’s Principle applies only to perfect, steady flows
- Pressure is higher in regions where fluid velocity is lower
- It provides the basis for devices like Venturimeters and explains airplane flight
- Understanding its limitations is critical for board questions






















