Learn Physics Class 11 Mechanical Properties Of Solids With Vedantu's Expert Guidance
FAQs on NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids
1. What can I expect from the NCERT Solutions for Class 11 Physics Chapter 8?
These solutions provide clear, step-by-step answers for all the exercise questions in Chapter 8, Mechanical Properties of Solids, as per the latest CBSE 2025-26 syllabus. They explain the correct formulas and methods for solving problems related to stress, strain, Young's modulus, bulk modulus, and shear modulus, helping you understand the concepts and score better in exams.
2. How do the NCERT solutions explain the concept of stress and strain?
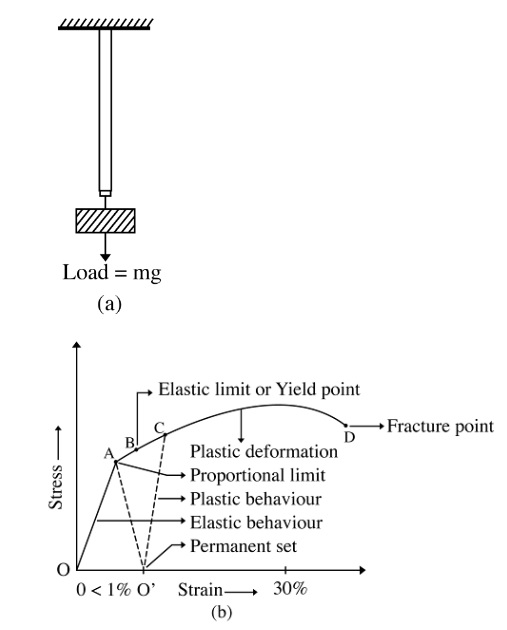
In the NCERT solutions, stress (σ) is defined as the internal restoring force acting per unit area of a deformed body. Strain is the fractional change in the dimension (length, volume, or shape) of the body. The solutions demonstrate how to calculate these values in different scenarios, such as a wire under tension or a cube under hydraulic pressure.
3. What is the correct method to solve problems using Hooke's Law as shown in the Chapter 8 solutions?
The solutions apply Hooke's Law, which states that within the elastic limit, stress is directly proportional to strain. The standard method is:
- Identify the type of stress (tensile, compressive, or shear).
- Choose the appropriate modulus of elasticity (Young's, Shear, or Bulk).
- Use the formula: Stress = Modulus × Strain.
- Substitute the known values and solve for the unknown quantity, ensuring all units are in the SI system.
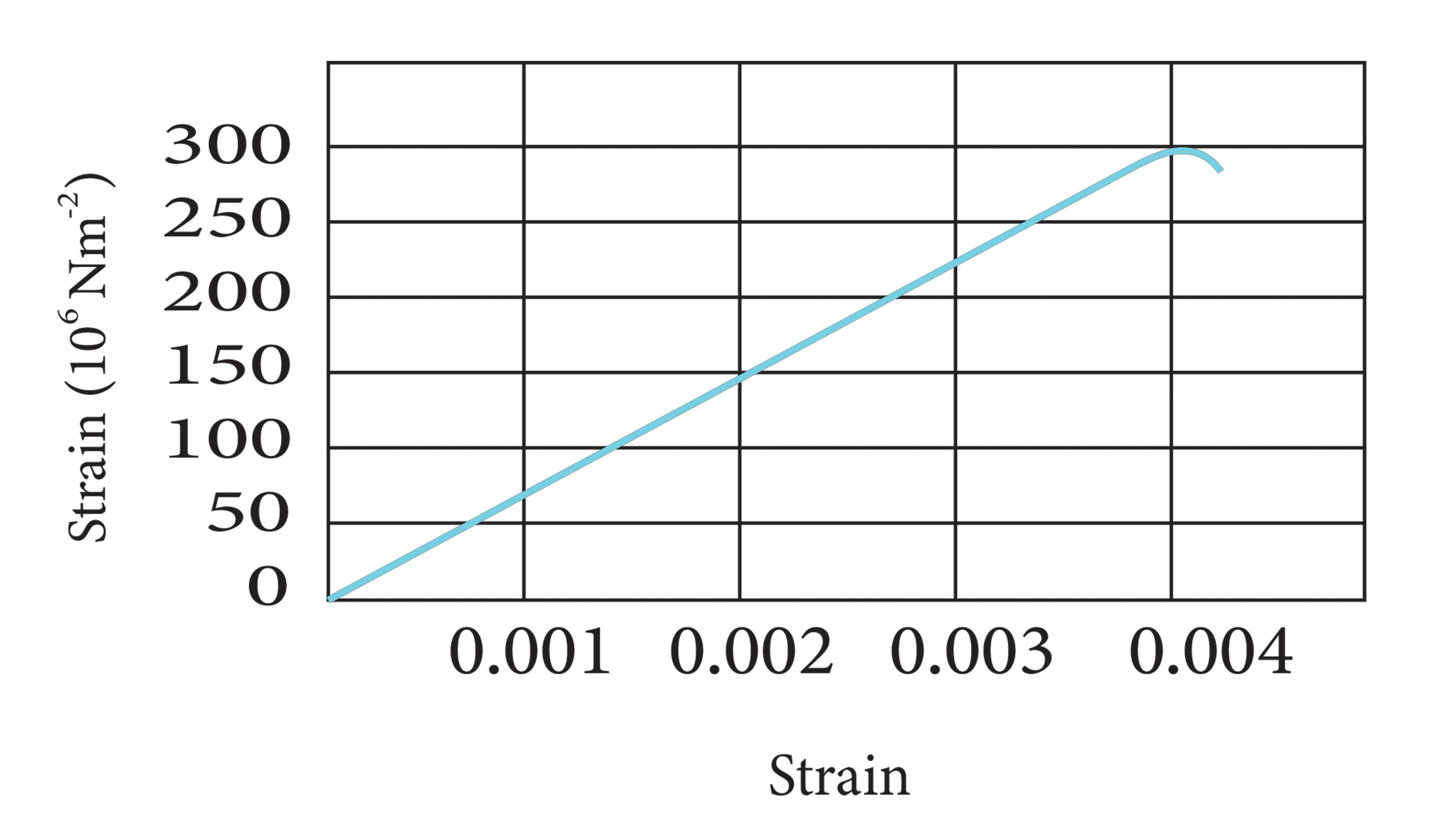
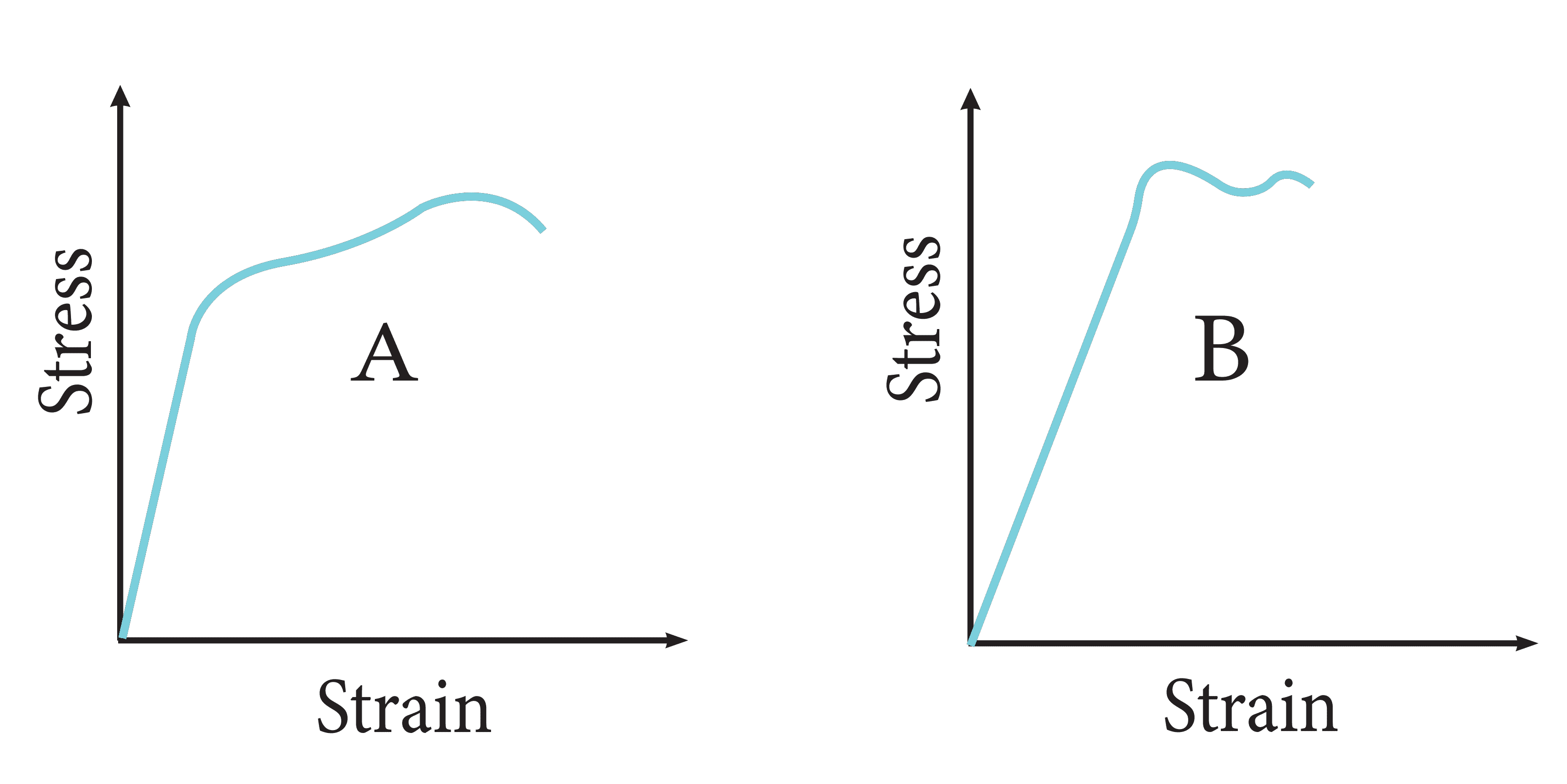
4. How do the NCERT solutions use the stress-strain curve to differentiate between ductile and brittle materials?
The NCERT solutions for problems involving stress-strain graphs show that ductile materials (like steel or copper) have a large plastic region, meaning they can undergo significant deformation before fracturing. In contrast, brittle materials (like glass) have a very small or non-existent plastic region and fracture soon after the elastic limit is crossed. The solutions use points on the graph to determine properties like yield strength and fracture point.
5. How do I calculate the elongation of a wire under a load, as demonstrated in the NCERT solutions?
To find the elongation (ΔL), the solutions use the formula for Young's Modulus (Y): Y = (F/A) / (ΔL/L). The step-by-step method is as follows:
- Calculate the total force (F) acting on the wire (e.g., mg).
- Determine the cross-sectional area (A) of the wire, usually πr².
- Rearrange the formula to solve for ΔL: ΔL = (F × L) / (A × Y).
- Ensure all values like original length (L), area (A), and Young's Modulus (Y) are in SI units before calculating.
6. Why is the stretching of a coil spring determined by its Shear Modulus and not Young's Modulus?
Although the spring elongates as a whole, the wire it is made of undergoes twisting or torsion, not a simple lengthwise stretch. This change in shape at a constant volume is a type of shearing strain. Therefore, the Shear Modulus (G), which measures a material's resistance to shape change, is the relevant property. Young's Modulus, which relates to longitudinal stress and strain, is not applicable here.
7. What is the step-by-step method to calculate the volume contraction of a solid under hydraulic pressure using the NCERT solutions?
The solutions use the concept of Bulk Modulus (B) to find volume change. The steps are:
- Identify the applied hydraulic pressure (p) and the original volume (V) of the object.
- Use the formula for Bulk Modulus: B = -p / (ΔV/V).
- Rearrange it to find the volume contraction (ΔV): ΔV = (p × V) / B.
- The negative sign indicates that volume decreases as pressure increases, but for calculation purposes, you typically work with the magnitudes.
8. According to the solutions for Chapter 8, what is a common mistake when comparing the Young's Modulus of two different materials?
A common pitfall is assuming that a more stretchable material like rubber has a higher Young's Modulus. The NCERT solutions clarify that Young's Modulus (Y) is a measure of stiffness, not stretchability. Since steel requires a much larger force for the same amount of strain compared to rubber, steel has a significantly higher Young's Modulus. The formula Y = Stress/Strain shows that for a given stress, Y is inversely proportional to strain.
9. How are the three types of elastic moduli—Young's, Shear, and Bulk—applied differently in the NCERT exercise problems?
The NCERT solutions apply each modulus based on the type of deformation:
- Young's Modulus (Y) is used for changes in length, such as stretching a wire.
- Shear Modulus (G) is used for changes in shape, like the vertical deflection of a cube's face when a tangential force is applied.
- Bulk Modulus (B) is used for changes in volume due to pressure from all sides, such as a solid submerged in a fluid.